Análisis de circuitos secuenciales

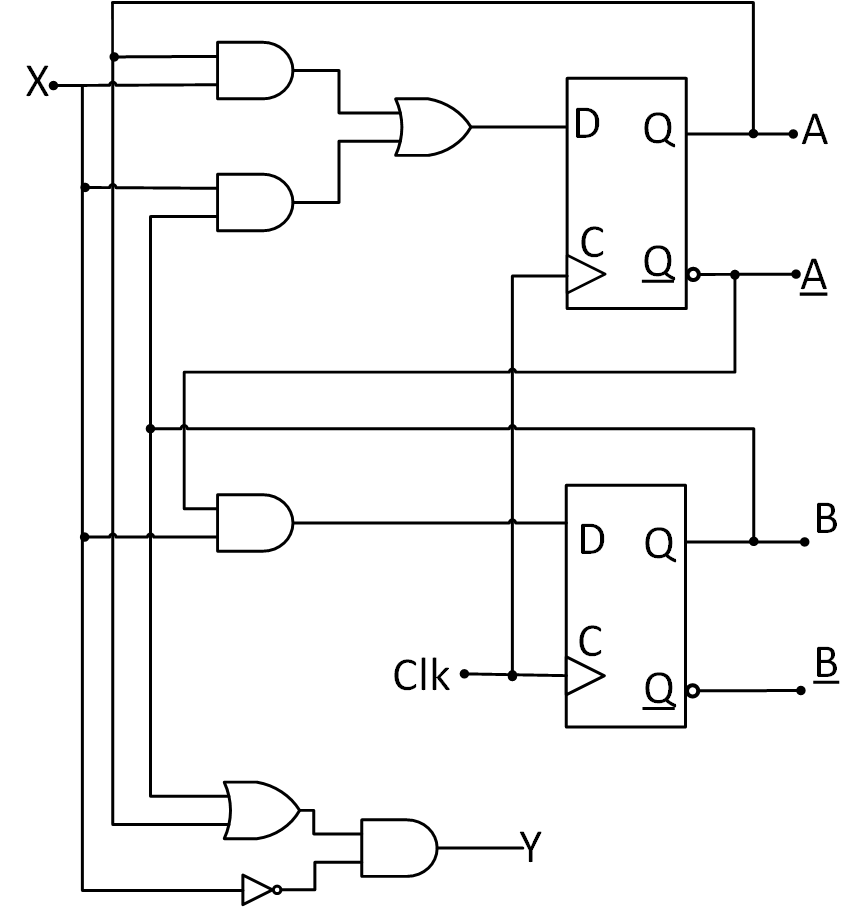
Las ecuaciones booleanas de entrada a los flip-flops son una expresión muy conveniente para especificar el diagrama lógico de un circuito secuencial. Es usual el determinar las entradas usando el nombre del tipo de flip flop que se utiliza en el circuito secuencial, estas expressiones también especifican de forma total el circuito combinacional que maneja a los elementos de memoria o flip-flops. En las ecuaciones booleanas de entrada no se especifica la entrada de reloj o \(CLK\), pero se entiende que es necesaria al ser parte de un circuito secuencial (Mano and Kime [MK17]). Por ejemplo, para el circuito secuencial que se muestra en la figura Figura 52 las ecuaciones de entrada son las siguientes:

\[\begin{split} \begin{eqnarray} D_A=AX+BX\\ D_B=\overline{A}X\\ Y=(A+B)\overline{X} \end{eqnarray} \end{split}\]

Las entradas \(D_A\) y \(D_B\) son las ecuaciones de entrada a dos flip-flops diferentes. Por otra parte, las salidas de los flip-flops son denotadas por las literales \(A\) y \(B\). Estas dos salidas constituyen el estado del circuito secuencial.

Figura 52 Circuito lógico secuencial (Mano and Kime [MK17]).

El código VHDL para la descripción de un flip-flop RS, usando estructuras de desición y un proceso basado en eventos para la inclusión de una entrada de reloj es la siguiente:

----------------------------------------------------
-- Descripción de un circuito secuencial, basado en 
--         flip-flop D
------------------------------------------------------
-- Primero se describe la entidad básica que es el 
-- flip-flop D
-----------------------------------------------------
library ieee;
use ieee. std_logic_1164.all;
use ieee. std_logic_arith.all;
use ieee. std_logic_unsigned.all;

entity ff_D is
PORT( D,CLK: in std_logic;
  Q: out std_logic;
noQ: out std_logic);
end ff_D;

architecture arq of ff_D is
begin
process(CLK)
begin
if(CLK='1' and CLK'EVENT) then
Q <= D;
noQ <= NOT D; 
end if;
end process;
end arq;
-----------------------------------------------------------------
----  Después se describe la estructura del circuito secuencial
---      completo, que incluye la parte combinacional
-----------------------------------------------------------------
library ieee;
use ieee. std_logic_1164.all;
use ieee. std_logic_arith.all;
use ieee. std_logic_unsigned.all;


entity secuencial is
PORT( X,CLK: in std_logic;
    Y: out std_logic);
end secuencial;

architecture arq of secuencial is

component ff_D
PORT( D,CLK: in std_logic;
  Q: out std_logic;
noQ: out std_logic);
end component;
signal A,noA,B,noB,DA,DB: STD_LOGIC;

begin


DA <= (A and X)or(B and X);
DB <= noA and X;
--- Mapeo de puertos con la interconexión de los flip-flops 
ff_A: ff_D port map(DA,CLK,A,NoA);
ff_B: ff_D port map(DB,CLK,B,noB);

Y <= (A or B)and (not X);
end arq;

La Tabla 19 constituye la tabla de estados del ciurcuito lógico secuencial mostrado en la Figura 52. La única entrada a este circuito secuencial es \(X\), para cada posible combinación de la entrada los estados aparecen repetidos, además, considerese que el estado futuro en la tabla refleja el valor lógico de las salidas \(A\) y \(B\) \(\textcolor{blue}{después~de~un~periodo~de~reloj}\). Cuando se obtiene una tabla de estados, se deben enumerar todas las posibles combinaciones binarias de estados actuales y entradas. En el caso de la Tabla 19 se tienen ocho combinaciones de entrada por que se tienen dos bits de estado \(A\) y \(B\), además de la entrada \(X\).

Tabla 19 Tabla de verdad del latch RS

	Estado Actual		Entrada		Estado futuro		Salida
	A	B	X		A	B	Y
	0	0	0		0	0	0
	0	0	1		0	1	0
	0	1	0		0	0	1
	0	1	1		1	1	0
	1	0	0		0	0	1
	1	0	1		1	0	0
	1	1	0		0	0	1
	1	1	1		1	0	0

La tabla de estado de un circuito secuencial con \(m\) flip-flops y \(n\) entradas requiere \(2^{m+n}\) filas para ser descrita. Para construir la tabla de estado, se enlistan con los números binarios desde \(0\) hasta \(2^{m+n}-1\) combinando columnas de entrada y de estado actual.