Diseño de circuitos secuenciales.#
El diseño de los circuotos lógicos secuenciales que son del tipo síncrono. es decir que cuenten con una entrada de reloj, se inicia regualrmente con un conjunto de especificiaciones que son del tipo verbal, abstracta o incluso de un conjunto de expresiones booleanas que a menudo surgen de un diagrama lógico incluso. A diferencia de la especificiación de un circuito combiancional que se especifica completamente por medio de una tabla de verdad, para un circuito secuencial se hace necesaria una tabla de estados como la especificada en la Tabla 19.
Un circuito secuencial se construye a partir de flip-flops y de una parte combinacional a partir de compuertas lógicas. Una parte importante del diseño consiste en elegir los flip-flips adecuados y encontrar las expresiones booleanas que en conjunto con la parte secuencial cumpla las especificaciones dadas. El número mínimo de flip-flops es determinado completamente por los estados del circuito; si se tienen \(n\) flip-flops pueden representar \(2^n\) estados binarios. Finalmente, se puede expresar que el porceso de diseño de un circuito secuencial se convierte en un problema de diseño de circuitos combinacionales, en el que pueden aplicarse las técnicas de diseño como el mapa de Karnauhg (Mano and Kime [MK17]).
Pasos principales de diseño.#
El diseño de circuitos secuenciales es muy similar al de los circuitos combinacionales, sim embargo se pueden aplicar algunas reglas similares para el diseño de los circuitod lógicos secuenciales, ya sean síncronos o asíncronos. Los siguientes pasos son generales mas no únicos para el diseño de circuitos combinacionales, como se desctibe en (Mano and Kime [MK17]):
Especificacion de diseño: se describe el desempeño o comportamiento deseado para el circuito o sistema digital.
Formulación del desempeño deseado: se obtiene o plantea un diagrama de estados o una tabla de estados a partir de las especificaciones de diseño.
Se asignan los estados: si es viable la costrucción de un diagrama de estados se asignan los códigos binarios a los estados de la tabla, entendidos como la combinación de las salidas de los flip-flops.
De determinan las expresiones booleanas de entrada: se seleccionan los flip-flops a partir de la tabla de estados, la tabla de estados puede ser una herramienta importante de selección del tipo de flip-flop en función de las expresiones de entrada que se encuentran íntimamente relacionadas o codificadas en los estados futuros.
Determinación de la ecuación de salida: se establecen las euaciones de salida a partir de las salidas que se establecen en las especificaciones de salida o salidas en la tabla de estados.
Optimización: se minimizan las expresiones de entrada y salida de los flip-flops usando herramientas como el mapa de Karnaugh.
Especificación del diagrama lógico se especifica el diagrama lógico del circuito secuencial usando los símbolos estándar para los flip-flops y las compuertas para las expresiones booleanas.
Simulación: por medio de la simulación se verifica el comportamiento del circuito lógico. La simualción se realiza utilizando las herramientas pertinentes, un simulador gráfico o un software de desarrollo como vivado.
El principio para formular las tablas y diagramas de estados es la comprensión intuitiva del concepto de estado. Un estado es un recordatorio de las combinaciones de entrada que se han aplicado al circuito en cualquier flanco positivo del reloj.
Diagramas de estados.#
La información disponible en una tabla de estados se puede representar gráficamente en forma de diagrama de estados. En este tipo de diagrama, un estado se representa por un círculo, y las transiciones entre los estados se indican mediante líneas orientadas que conectan los círculos. Lo anterior en el entendido de que los estados son las salidas de los flip-flops de los cuales se compone el circuito lógico secuencial. El diagrama de estados proporciona la misma información que la tabla de estados y se obtiene directamente de él.
Autómatas de Moore y autómatas de Mealy
Los circuitos secuenciales en los que las salidas dependen de las entradas, así como de los estados presentes, se denominan Autómatas o Máquinas de Mealy.
Para especificar los circuitos secuenciales en los que las salidas sólo dependen de los estados actuales, basta con una única columna. A estos circuitos secuenciales se les denomina Autómatas de Moore.
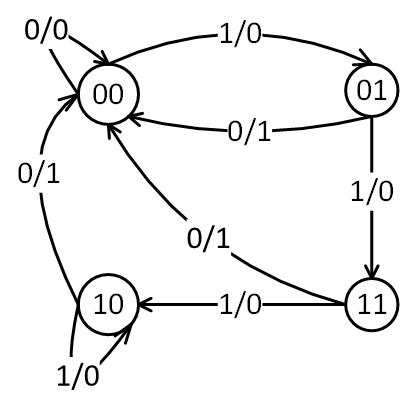
En la Figura 53 se muestra la representación en un diagrama de estados del comportamiento del circuito lógico de la figura Figura 52
El número binario dentro de los círculos de un diagrama de estados indica el valor binario de las salidas de los flip-flops. En los autómatas o máquinas de estados tipo Mealy, las líneas o conectores que unen a dos estados se etiquetan con dos números binarios separados por una barra /, de manera que el valor se la entrada durante el estado actual se escribe antes de la barra y el siguiente valor es la salida durante el estado actual cuando se aplica tal entrada. Por ejemplo, el conector que une al estado \(00\) con el estado \(01\) se etiqueta como \(1/0\), esto significa que cuando el ciruito secuencial bajo análisis sen encuentra en el estado actual \(00\) y la entrada es \(1\), la salida es \(0\). Despues del siguiente flanco positivo de reloj, el circuito cambia al siguiente estado \(01\). Cuando se usa un conector que conecta a un círculo en un diagrama de estados consigomismo indica que no hay cambio en los estados.
No hay ninguna diferencia entre la información que proporciona una tabla de estados y la que proporciona un diagrama de estado La interpretación del diagrama de estados mostrado en la Figura 53 es la siguiente: El funcionamiento del circuito empieza cuando se toma en consideración al estado \(00\) como el punto de partida o estado inicial. Siempre que la entrada permanece en un valor de \(1\) lógico, la salida permanece en \(0\). Si se encuentra el circuito en el estado \(01\), una entrada igual a \(0\) con una salida igual a \(1\), regresa al circuito a su estado inicial \(00\).
Descripcion en VHLD usando estados#
La descripción en VHDL del circuito mostrado en la Figura 52 se muestra abajo:
------------------------------------------------------------
-- Descripción de un circuito secuncial usando estados
------------------------------------------------------------
library ieee;
use ieee. std_logic_1164.all;
entity secuencial is
PORT( X,CLK: in std_logic;
Y: out std_logic);
end secuencial;
architecture arq of secuencial is
TYPE STATE_TYPE is (e0,e1,e2,e3);
signal estado: STATE_TYPE;
signal A,noA,B,noB: std_logic;
begin
PROCESS(CLK)
begin
if CLK'event AND CLK='1' then
case estado is
when e0=>
if X='1' then
Y<='0';
estado <= e1;
A <='0';
noA <= '1';
B <= '1';
noB <= '0';
else
Y<='0';
estado <= e0;
A <='0';
noA <= '1';
B <= '0';
noB <= '1';
end if;
when e1=>
if X='1' then
Y<='0';
estado <= e3;
A <='1';
noA <= '0';
B <= '1';
noB <= '0';
else
Y<='1';
estado <= e0;
A <='0';
noA <= '1';
B <= '0';
noB <= '1';
end if;
when e2=>
if X='1' then
Y<='0';
estado <= e2;
A <='1';
noA <= '0';
B <= '0';
noB <= '1';
else
Y<='1';
estado <= e0;
A <='0';
noA <= '1';
B <= '0';
noB <= '1';
end if;
when e3=>
if X='1' then
Y<='0';
estado <= e2;
A <='1';
noA <= '0';
B <= '0';
noB <= '1';
else
Y<='1';
estado <= e0;
A <='0';
noA <= '1';
B <= '0';
noB <= '1';
end if;
when others =>
Y<='U';
A<='U';
noA<='U';
B<='U';
noB<='U';
end case;
end if;
end PROCESS;
end arq;
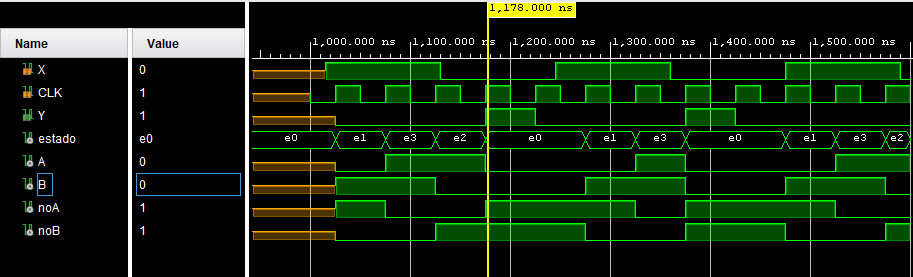
La salida de la simulación del código anterior se muestra en la Figura 54.