Circuitos lógicos aritméticos

En los sistemas digitales como los microcontroladores y las computadoras se emplean circuitos lógicos diseñados para realizar operaciones areitméticas como sumas, sumas-restas, y multiplicaciones. También se emplean, incrementadores y decrementadores de datos digitales. En esta sección se analizan los sumadores y su descripción en VHDL

El semi-sumador

Un semi-sumador es un circuito lógico aritmético que efectúa la suma de dos dígitos binarios. El circuito semi-sumador tiene dos entradas y dos salidas. Las variables de entrada son los sumandos, y por las variables de salida se obtienen la suma y el acarreo. Se asignan los símbolos X e Y a las dos entradas y S (por Suma) y C (por acarreo, o Carry en inglés) a las salidas (Mano and Kime [MK17]). La tabla de verdad para el semisumador se muestra en la Tabla 7. La salida C sólo es «»1»» cuando ambas entradas son «»1»». La salida S representa el bit menos significativo de la suma.

Tabla 7 Tabla de verdad de un circuito semi-sumador

Entradas		Salidas
X	Y	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Las funciones booleanas para las dos salidas, obtenidas fácilmente de la tabla de verdad, son:

\[ S=\overline{X}Y+X\overline{Y}=X \oplus Y \]

\[ C=XY \]

El diagrama del circuito lógico resultante se muestra a continuación:

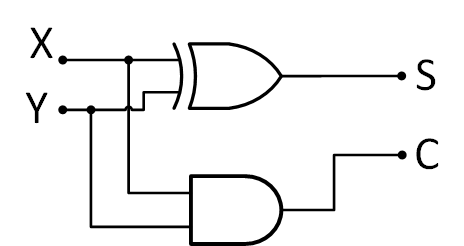
Figura 12 Circuito lógico semi-sumador.

La descripción en VHDL del semi-sumador es la siguiente:

-------------------------------------------------------------------------------
-- Descripción VHDL de un semi-sumador
-------------------------------------------------------------------------------
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
 
entity semi_sumador is
  port (
    X  : in std_logic;
    Y  : in std_logic;
    S  : out std_logic;
    C  : out std_logic
    );
end semi_sumador;
 
architecture arq of semi_sumador is
begin
  S  <= X xor Y;
  C <= X and Y;
end arq;

La salida en Vivado de la simulación se muestra en la figura Figura 13.

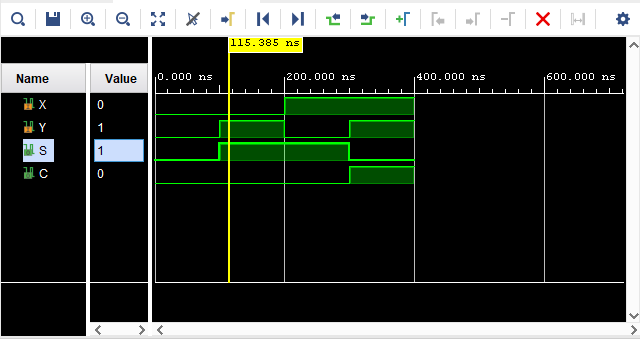
Figura 13 Simulación del semi-sumador.

El sumador completo

Un sumador completo es un circuito lógico combinacional que efectúa la suma aritmética de tres bits de entrada. Además de las tres entradas, tiene dos salidas. Dos de las variables de entrada, denominadas como X e Y, representan los dos bits significativos a sumar. La tercera entrada, Z, representa el acarreo que procede de la posición anterior menos significativa. Se necesitan dos salidas porque la suma aritmética de tres bits puede tomar valores entre 0 y 3, además de que la reperesentación en binario de 2 y de 3 necesita dos bits (\(2_{10}=10_2\) y \(3_{10}=11_2\)). Igual que en el caso del semisumador, las dos salidas se designan por los símbolos S para suma y C para acarreo (Carry); la variable binaria S proporciona el valor del bit de la suma, mientras que de la variable binaria C se obtiene el acarreo de salida (Mano and Kime [MK17]). La tabla de verdad del sumador completo se lista en la Tabla 8.

Tabla 8 Tabla de verdad de un circuito semi-sumador

		Entradas	Salidas
X	Y	Z	C	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Los mapas de Karnaugh para las variables de salida S y C se muestran en la Figura 14 y la Figura 15.

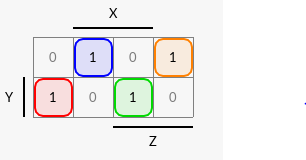
Figura 14 Mapa de Karnaugh de la variable S.

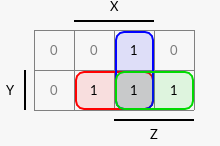
Figura 15 Mapa de Karnaugh de la variable C.

De los mapas anteriores se concluye que las expresiones booleanas para las salidas S y C son:

\[ S=\overline{X}~\overline{Y}Z+\overline{X}Y\overline{Z}+X\overline{Y}~\overline{Z}+XYZ \]

\[ C=XY+XZ+YZ \]

Estas dos expresiones booleanas se pueden simplificar como:

(1)\[\begin{split}\begin{eqnarray} S=X \oplus Y \oplus Z\\ C=XY+Z(X+Y) \end{eqnarray}\end{split}\]

Donde el operador \(\oplus\) equivale a la operación XOR. El código VHDL para el sumador completo es el siguiente:

El diagrama lógico del sumador completo se muestra en la Figura 16.

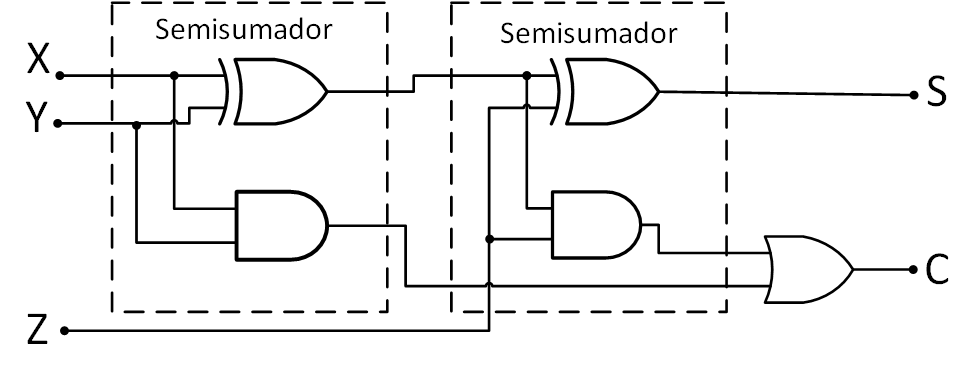
Figura 16 Circuito sumador completo

El código VHDL para la descripción del sumador completo es el siguiente:

------------------------------------------------
-- Descripción de un circuito sumador completo
-----------------------------------------------
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
 
entity sumador_completo is
  port (
    X  : in std_logic;
    Y  : in std_logic;
    Z  : in std_logic;
    S  : out std_logic;
    C  : out std_logic
    );
end sumador_completo;
 
architecture arq of sumador_completo is
begin
  S  <= (X xor Y xor Z);
  C <= (X and Y) or (Z and (X or Y));
end arq;

La salida de la simulación en vivado es:

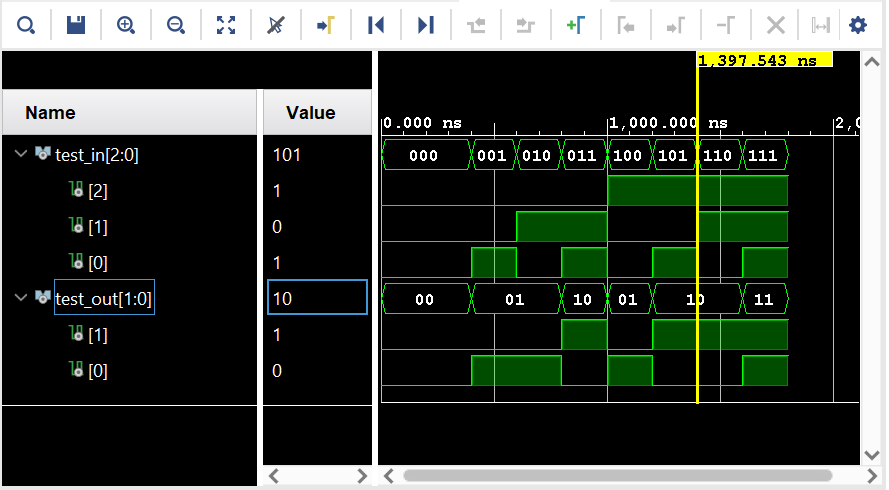
Figura 17 Simulación del sumador completo.