Práctica 1: Primeros pasos#
En esta práctica se utilizan comandos básicos de MATLAB® y un ejemplo sencillo de solución de un sistema de ecuaciones, utilizando matrices. Las instrucciones que se tratan en esta sección se introducen en el command window (ver Figura 6) de la interfaz principal de MATLAB®.
Figura 6 Ventana de comandos (Command window)#
Operaciones y comandos básicos#
A continuación se enlistan los comandos básicos que se usan comúnmente en la ventana de comandos (command window) de MATLAB®.
1.-Limpiar pantalla de comandos: >>clc
2.-Limpiar las variables almacenadas en memoria: >>clear
3.-Despliegue de información de las variables: >>whos
4.-Cerrar todas las gráficas de datos: >>close all
En MATLAB®, tanto en la ventana de comandos como en el editor de textos, el símbolo de porcentaje «%» se utiliza para escribir comentarios .
Nota
Es posible copiar el código directamente de este cuadernillo y pegarlo en el command window de MATAB$B, en el editor de MATLB®B o cualquier otro editor de texto, utilizando la opción de copiar al portapapeles, disponible en cada recuadro con código escrito.
a=3 %Asignación del valor 3 a la variable a
a = 3
Como se puede observar en la salida, el comentario al lado de la instrucción a=3 no se despliega
en la ventana de comandos. Para desplegar texto en el command window se usa la función interna de MATLAB® disp("mensaje"). A continuación se presentan ejemplos de los resultados del uso de comandos
y operaciones comunes en MATLAB®:
1.- Creación de variables y asignación de valores numéricos: a=3;b=45;
2.- Multiplicación: a*b
3.- Suma: a+b
4.- Resta: a-b
5.-División:a/b
6.-Potencia: a^b (a elevado a la potencia b)
7.- Raíz cuadrada: sqrt(b)
Para reproducir estas operaciones, se puede copiar y pegar el conjunto de instrucciones siguiente en el command wondow de MATLAB®.
clear
a=3 % Creación de variables y asignación de valores numéricos
b=45 %
disp("Multiplicación a*b")
a*b
disp("Suma a+b")
a+b
disp("Resta a-b")
a-b
disp("División a/b")
a/b
disp("Potencia a^b (a elevado a la potencia b)")
a^3
disp("Raiz cuadrada de a")
sqrt(b)
a = 3
b = 45
Multiplicación a*b
ans = 135
Suma a+b
ans = 48
Resta a-b
ans = -42
División a/b
ans = 0.0667
Potencia a^b (a elevado a la potencia b)
ans = 27
Raiz cuadrada de a
ans = 6.7082
Una instrucción muy útil es la de limpiar pantalla, esto permite borrar resultados anteriores para evitar la saturación de datos desplegados.
clc
También se puede desplegar información de las variables creadas y su tamaño en memoria
whos
Name Size Bytes Class Attributes
a 1x1 8 double
ans 1x1 8 double
b 1x1 8 double
close all
El comando clear limpiará las variables creadas en la ejecución de los comandos anteriores. Fácilmente se puede comprobar lo anterior usando un comando clear, seguido de un comando whos, esto producirá una salida vacía que indica que no hay variables en el espacio de trabajo o workspace.
clear
whos
Conversión de grados Celsius a Farenheit#
Es posible realizar la conversión de un conjunto de datos en un sistema de unidades a otro usando variables tipo arreglo en MATLAB®. Haremos un ejemplo de la conversión a grados Farenheit de un conjunto de datos almacenados en un arreglo en las siguientes líneas de código. Se crea el conjunto de datos en grados Centígrados \(-4<°C<4\) con incremento de \(1\) \(°C\), para tener un total de 10 datos.
C=[-4:1:4];
La fórmula para la conversión de grados Centígrados a Farenheit es:
En MATLAB®, la operación se realiza en el vector completo.
F=(9/5)*C+32;
Se puede desplegar la información en forma de tabla si se crea una variable tipo matriz para tal efecto.
Tabla_conv=[C' F']
Tabla_conv = 9×2 double
-4.0000 24.8000
-3.0000 26.6000
-2.0000 28.4000
-1.0000 30.2000
0 32.0000
1.0000 33.8000
2.0000 35.6000
3.0000 37.4000
4.0000 39.2000
La comilla simple se usa para generar la versión transpuesta de un vector o matriz, es decir, se puede convertir un vector fila en un vector columna, por ejemplo:
V=[1 -1 3]
V = 1×3 double
1 -1 3
Su versión transpuesta \(V^{T}\) es
V'
ans = 3×1 double
1
-1
3
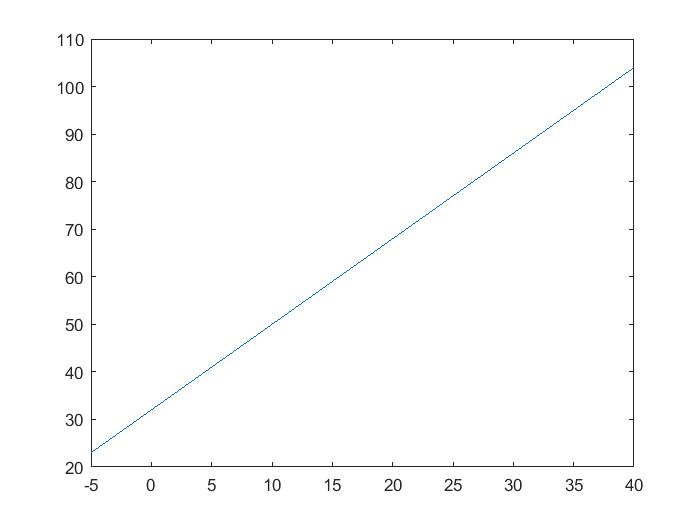
En caso de ser necesario, es posible hacer la conversión de grados Centígrados a Farenheit con una mayor resolución, de manera tal que en vez de mostrar una tabla de conversiones se puede mostrar una gráfica. Por ejemplo, para en rango de grados Centígrados \(-4<°C<40\) con incremento de \(0.5\) \(°C\), para tener un total de 91 pares de datos, en MATLAB® se expresa lo siguiente:
C=[-5:0.5:40];
Se hace la conversión a grados Farenheit como en el caso anterior, usando la Ecuación (1)
F=(9/5)*C+32;
Se hace una gráfica de °F contra °C, con la instrucción plot() en la que se introduce la variable independiente y la variable dependiente separadas por una coma
figure
plot (C,F) %Gráfica
Generación de gráficas de funciones#
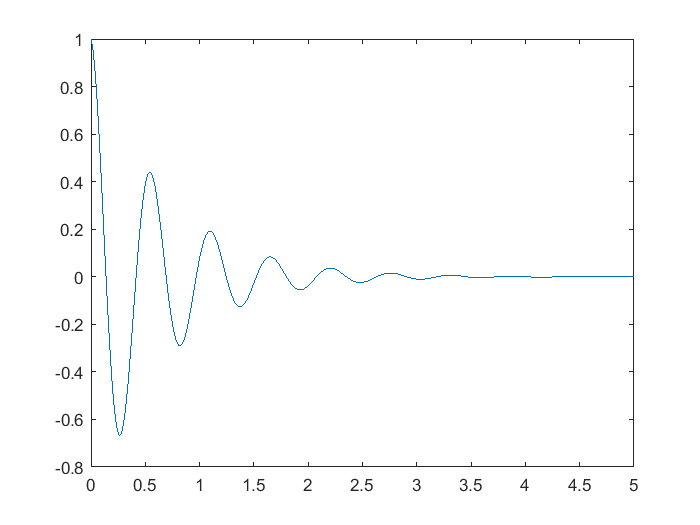
Para generar la gráfica de una función en MATLAB®, se crean dos vectores; uno con la variable independiente y un segundo con la variable independiente, por ejemplo, para graficar la función del tiempo, expresada en la ecuación siguiente:
Se genera un vector de tiempo en el intervalo definido como \(0<t<5\) con un incremento \(\Delta t=0.001\)
t=[0:0.001:5];
Después se genera la variable independiente \(y(t)\) evaluando la función con operadores multiplicación y exponencial
y=exp(-1.5*t).*cos(11.35*t);
El punto antes del operador multiplicación (.*) se utiliza cuando se trabaja con vectores y no con variables constante o escalares
Se genera la gráfica usando la instrucción plot
plot(t,y)
Resolver un sistema de ecuaciones usando MATLAB®#
El siguiente ejemplo muestra como utilizar MATLAB® para resolver un sistema de ecuaciones de tres incógnitas. Considere el sistema de tres ecuaciones con tres incógnitas de la Ecuación (3)
Para resolver el sistema de ecuaciones, se plantea La forma matricial del sistema de ecuaciones, de la forma:
Donde \(A\) es la matriz de coeficientes y \(B\) el vector de resultados.
A continuación se construye la matriz y el vector usando los comandos de MATLAB®:
A=[3 2 -5;1 0.5 3;-2 7 -3]
A = 3×3 double
3.0000 2.0000 -5.0000
1.0000 0.5000 3.0000
-2.0000 7.0000 -3.0000
Para crear el vector de coeficientes:
B=[10;5;-2]
B = 3×1 double
10
5
-2
La solución del sistema de ecuaciones se encuentra al realizar la operación matricial:
X=inv(A)*B
X = 3×1 double
3.4097
0.8546
0.3877
De manera alternativa, dado que \(A^{-1}\) es la inversa de la matriz \(A\), se puede usar el comando inv(A), de manera que la solución se puede calcular como:
X=(A^-1)*B
X = 3×1 double
3.4097
0.8546
0.3877
De manera que el valor numérico de las variables es:
Es fácil comprobar que estos valores satisfacen el sistema de ecuaciones si se realizan las sustituciones en el sistema de ecuaciones original:
% Ecuacion (1) 3x+2y-5z
3*(3.4097)+2*(0.8546)-5*(0.3877)
ans = 9.9998
% Ecuacion (2) x+0.5y+3z
1*(3.4097)+0.5*(0.8546)+3*(0.3877)
ans = 5.0001
% Ecuacion (3) -2x+7y-3z
-2*(3.4097)+7*(0.8546)-3*(0.3877)
ans = -2.0003
Ejercicios#
Escriba en un archivo .m, almacenado en su carpeta de trabajo y con un nombre válido, un programa en el que se realicen los siguientes ejercicios y problemas:
1.- Defina un vector \(v=[1.8~-2.3~~3.5]\) y una matriz \(A=\begin{bmatrix} 3.5 & 12.34 & -15\\ 1.34 & 4.25 & 6.37\\ -2.45 & 7.8 & -9.3 \end{bmatrix}\). como dos variables distintas.
2.- Almacene en un vector el resultado de sumar 2.5 al vector \(v\)
3.- Realice la operación \(sen(4A)\).
4.- Despliegue la gráfica de la función \(y=5.4x^3-2.4x^2+3.6x+2.2\) en el intervalo \([-15,15]\) con un incremento de \(0.001\).
5.- Convierta de grados Farenheith a Celsius el conjunto de temperaturas contenidas en el intervalo \([19,72]\) con incremento uniforme de 2.5 °F.
5.- Resuelva el sistema de ecuaciones:
usando operaciones matriciales.
