Práctica 4: Estructuras de control de flujo del programa

La instrucción find() es muy útil para seleccionar datos que complen con ciertas características en un conjunto más grande. Las instrucciones de comparación <=, <=, ==, etc. son suficientes para determinar funciones definidas a pedazos y para construir arreglos con datos que cumplen con ciertas características a partir de un arreglo más general, sin embargo, a menudo es necesario hacer uso de estructuras más complejas para controlar el flujo de ejecución de un programa. Una de estas estructuras es la conocida como if.

Estructura if

La estrutura if tiene la forma:

if(expresión de comparación)

end

Si la expresión entre parénteis (expresión de comparación) es verdadera, entonces se ejecuta el conjunto de instrucciones que se situa entre los enunciados if y end. Para dar legilibilidad al código se usa una práctica conocida como indentado, es decir, usar una sangría para que los enunciados de instrucciones queden perfectamente identificados del resto del flujo de programa. En MATLAB®, es indiferente el indentado o sangría en el código, por lo tanto las instrucciones se ejecutan sin problema, pero su legibilidad mejora constantemente.

Un ejemplo de aplicación de la estructura de control de flujo de programa if es la siguiente:

a=4;

if(a>3)
  disp("a es mayor que 3")
end 

if(a<0)
  disp("a es negativo")
end 

a es mayor que 3

Estructura if/else

En general, las estructuras if funcionan mejor con escalares o valores lógicos. Un complemento a la estructura if es la estructura if/else, un ejemplo de aplicación de esta estructura es la siguiente:

if(a>0)

else

end

Como ejemplo, probaremos la estrucura propuesta para dos casos, uno para a=2

a=2;

if(a>0)
   raiz_cuadrada=sqrt(a)
else
   disp("error, la raiz cuadrada de un número negativo no es un número real")
end

raiz_cuadrada = 1.4142

y otro caso para a=-3:

a=-3;

if(a>0)
   raiz_cuadrada=sqrt(a)
else
   disp("error, la raiz cuadrada de un número negativo no es un número real")
end

error, la raiz cuadrada de un número negativo no es un número real

Cuando se trata con arreglos la isntrucción if se ejecutará para cada elemento del arreglo, por ejemplo, para un arreglo numero=[-4:1:4] se prueba la estructura anterior:

numero=[-4:1:4];

if(numero>0)
   raiz_cuadrada=sqrt(a)
else
   disp("error, la raiz cuadrada de un número negativo no es un número real")
end

error, la raiz cuadrada de un número negativo no es un número real

Como se puede observar, la instrucción solo se ejecuta si todos y cada uno de los elementos del arreglo cumplen con la condición de control dentro del paréntesis, una prueba más ilustrará esta situación:

numero=[1:1:4];

if(numero>0)
   raiz_cuadrada=sqrt(numero)
else
   disp("error, la raiz cuadrada de un número negativo no es un número real")
end

raiz_cuadrada = 1×4 double
    1.0000    1.4142    1.7321    2.0000

Si uno solo se los valores del arreglo fuera negativo, la estructura del programa lleva el control del flujo de ejecución a las instrucciones ubicadas después de la palabra else:

numero=[1 2 -3 4];

if(numero>0)
   raiz_cuadrada=sqrt(numero)
else
   disp("error, la raiz cuadrada de un número negativo no es un número real")
end

error, la raiz cuadrada de un número negativo no es un número real

Estructura elseif

Una estructura elseif permite comprobar varios criterios de forma anidada, manteniendo una importante pulcritud y órden en el código, un ejemplo de lo anterior se ilustra como sigue:

if(a>0)

elseif(a<3)

elseif(a<5)

else

end

De nuevo, cuado se trata de arreglos, cada uno de los elementos del arreglo deben cumplir con los criterios para que se ejecute el conjunto de instrucciones que le corresponde. A continuacón se presentan los ejemplos correspondientes.

a=3;

if((a>0)&(a<3))
   disp("a es un número positivo")
elseif((a>=3)&(a<5))
   disp("a está en el intervalo 3<a<5")
elseif((a>=5)&(a<7))
   disp("a está en el intervalo 5<a<7")
else
  disp("a está fuera del intervalo 0<a<7")
end

a está en el intervalo 3<a<5

Estructura Switch/case

La estructura de control de flujo de programa switch/case permite tomar decisiones en base a criterios, de forma parecida a lo que se realiza usado estructuras else/if pero de forma más ordenada y directa. Es posible establecer como criterios de desición a escalares o cadenas de caracteres. La estructura Switch/case tiene la estructura:

switch(variable)

case opción 1

case opción 2

case opción N

otherwise

end

Por ejemplo, para una cadena de caracteres o string, sucede lo siguiente:

animal="águila"

switch(animal)
   case "cocodrilo"  
       disp("Es un dinosaurio no aviano")   
   case "águila"  
         disp("Es un dinosaurio aviano")
   case "jaguar"
        disp("Es un mamífero")    
   otherwise
        disp("Ninguno de los anteriores") 
end

animal = "águila"

Es un dinosaurio aviano

Estructuras tipo bucle

Las estructuras bucle permiten realizar operaciones repetitivas, o dicho de otra manera, permiten realizar el mismo conjunto de instrucciones muchas veces sin la necesidad de escribirlo muchas veces. Las dos estructuras de repetición básicas en MATLAB® son el ciclo For y la sentencia While. El ciclo For tiene la siguiente etructura:

For(indice)

end

Si el índice es un arreglo, las instrucciones se ejecutan para cada elemento del arreglo, por ejemplo:

for k=[2 4 5]
    k=k
end

k = 2

k = 4

k = 5

Usualmente, el ciclo For se define con los parámetros, valor inicial, valor final e incremento, por ejemplo, para realizar la suma de los primeros 100 números, se puede usar un ciclo for:

suma=0;
for k=1:100
    suma=suma+k;
end
disp("La suma de los primeros 100 números enteros es:")
suma

La suma de los primeros 100 números enteros es:

suma = 5050

Se puede comprobar este resultado si se usa la fórmula descubierta por Gauss:

\[ \begin{equation} \sum^{n}_{k=1}k=\frac{n(n+1)}{2} \end{equation} \]

suma=100*(100+1)/2

suma = 5050

Otro ejemplo clásico es el cálculo del valor promedio de un conjunto de datos. El promedio de un conjunto de \(n\) datos se obtiene mediante la expresión:

\[ \begin{equation} promedio=\frac{1}{n}\sum^{n}_{k=1}d_k \end{equation} \]

donde \(n\) es el número total de los datos y \(d_k\) es cada uno de los datos individuales. Por ejemplo, para calcular la temperatura promedio de un conjunto de mediciones de 10m días se usa el siguiente conjunto de líneas de código:

T=[25 22 23 26 30 31 24 22 20 19];
n=length(T)
suma=0;

for k=1:n
   suma=suma+T(k);
end

promedio=suma/n

n = 10

promedio = 24.2000

La instrucción length() entrega como resultado el tamaño total de un arreglo. Una instrucción nativa de MATLAB® para el cálculo del promedio de un conjunto de datos es el comando mean(). Para encontrar el promedio de las temperaturas anteriores se usa de la siguiente manera:

T=[25 22 23 26 30 31 24 22 20 19];
promedio=mean(T)

promedio = 24.2000

Un ciclo while son similares a los bucles for. La diferencia importante es la forma en que se determina cuántas veces se repite el bucle. Los bucles while se ejecutan hasta que se satisface algún criterio. La estructura para un ciclo while es la siguiente:

while(condición)

end

Un ejemplo básico es el siguiente:

i=0;

while(i<5)
   i=i+1
end

i = 1

i = 2

i = 3

i = 4

i = 5

Por ejemplo, se puede usar un ciclo while para calcular el factorial de un número. El factorial de un número se calcula como:

\[ a!=a(a-1)! \]

Recordando que \(0!=1\), entonces, para calcular el factorial de 10, con un ciclo while se usan las instrucciones:

a=10;

k=1;
fac=1;

while(k<a)
   k=k+1;
   fac=fac*k;
end

disp("10!=")
fac

10!=

fac = 3628800

Para comprobar la operación realizada usando el ciclo while se usa la función nativa factorial() de MATLAB®

factorial(10)

ans = 3628800

Cálculo de sumatorias

Un ejemplo del uso de los bucles es, por excelencia, el cálculo de sumatorias simples y dobles, por ejemplo

\[ \begin{equation} \sum^{5}_{k=1}\left(k-2\right)\left(k^2-4\right) \end {equation} \]

La expansión de la serie es la siguiente:

\[\begin{split} \begin{eqnarray} \sum^{5}_{k=1}&=\left(1-2\right)\left(1^2-4\right)+\left(2-2\right)\left(2^2-4\right)+\left(3-2\right)\left(3^2-4\right)+\left(4-2\right)\left(4^2-4\right)+\left(5-2\right)\left(5^2-4\right)\\ &=3+0+5+24+63=95 \end {eqnarray} \end{split}\]

Es claro que la expansión de la serie resulta muy extensa para índices superiores a 5, en MATLAB®, la instrucción de bucle for permite el cálculo de la sumatoria anterior de manera muy compacta:

sumatoria=0;% Se inicializa la variable sumatoria que almacenará el resultado
for k=1:5
    sumatoria=sumatoria+(k-2)*(k^2-4);% Se calcula la sumatoria, el índice que aumenta es k
end
sumatoria% se despliega el resultado de la sumatoria final

sumatoria = 95

Cuando se tienen sumatorias dobles, el calculo de la sumatoria se interpreta como dos intrucciones de bucle anidadas, es decir una dentro de otra. Por ejemplo, considere la sumatoria doble:

\[ \begin{equation} \sum^{3}_{i=1}\sum^{2}_{j=1}\frac{(2i-3)}{(3+2j)} \end {equation} \]

Al desarrollar la sumatoria y calcular cada término por separado

\[ \begin{equation} \sum^{3}_{i=1}\sum^{2}_{j=1}=\left[(2(1)-3)+(2(2)-3)+(2(3)-3)\right]\sum^{2}_{j=1}\frac{1}{(3+2j)} \end {equation} \]

\[ \begin{equation} \sum^{3}_{i=1}\sum^{2}_{j=1}\frac{(2i-3)}{(3+2j)}=\left(3\right)\left[\frac{1}{(3+2(1))}+\frac{1}{(3+2(2))}\right]=\left(3\right)\left[\frac{1}{5}+\frac{1}{7}\right]=3\left[\frac{12}{35}\right]=1.0286 \end {equation} \]

suma=0;
for i=1:3
  for j=1:2
      (2*i-3)/(3+2*j);
      suma=suma+(2*i-3)/(3+2*j);
   end
end
suma

suma = 1.0286

La serie trigonométrica de Fourier

Sea \(x(t)\) una señal periódica, es decir que se puede expresar como \(x(t)=x(t+T)\), donde \(T\) es el periódo de dicha señal en segundos. Según lo descubierto por Joseph Fourier (Kamen and Heck [KH07]), una señal periódica se puede representar como la sumatoria de una infinidad de términos seno y coseno, usando la siguiente expresión:

(6)\[\begin{equation} x(t)=a_0+\sum^{\infty}_{k=1}\left[a_kcos(k\omega_0t)+b_ksen(k\omega_0t)\right],~~-\infty<t<\infty \end{equation}\]

donde \(\omega_0=\frac{2\pi}{T}\) y los términos \(a_0\), \(a_k\) y \(b_k\) se calculan como

(7)\[\begin{equation} a_0=\frac{1}{T}\int^{T}_{0}x(t)dt \end{equation}\]

(8)\[\begin{equation} a_k=\frac{2}{T}\int^{T}_{0}x(t)cos(k\omega_0t)dt \end{equation}\]

(9)\[\begin{equation} b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt \end{equation}\]

Es posible obtener la aproximación de una función del tiempo en términos de una serie trigonmétrica de Fourier en MATLAB® usando instrucciones de ciclo for. Por ejemplo, considere la señal tipo diente de sierra, definida por la expresión:

(10)\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} 150(t+0.02) & si & -0.02 \leq t \leq -0.01 \\ \\ 150t & si & -0.01 \leq t \leq 0.01 \\ \\ 150(t-0.02) & si & 0.01 < t \leq 0.03 \end{array} \right. \end{equation}\end{split}\]

se puede obtener su gráfica en MATLAB® mediante las líneas de código siguientes:

t=[-0.03:0.0001:0.03];
g=(150*(t+0.02)).*((t>=-0.03)&(t<-0.01))+(150*t).*((t>-0.01)&(t<=0.01))+(150*(t-0.02)).*((t>0.01)&(t<=0.03));

plot(t,g);
xlabel("t");
ylabel("g(t)")
axis([-0.03 0.03 -1.8 1.8]) %La istrucción axis ajusta los ejes de la gráfica
grid;

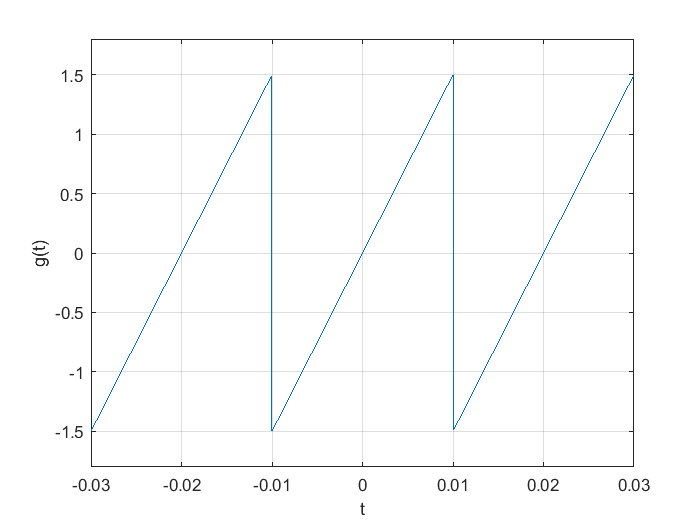
Los coeficientes \(a_0\), \(a_k\) y \(b_k\) para la serie trigonométrica de Fourier de la señal diente de sierra, definida por la ecuacion (10) se calculan usando las ecuaciones (7), (8) y (9). Dado que \(T=0.02\) y \(\omega_0=100\pi\):

\[\begin{equation}\nonumber a_0=\frac{1}{T}\int^{T}_{0}x(t)dt=\frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}x(t)dt=\frac{1}{0.02}\int^{-0.01}_{0.01}150tdt=7500\left[{\frac{t^2}{2}}_{t=-0.01}^{t=0.01}\right]=0 \label{a0sierra} \end{equation}\]

\[\begin{equation}\nonumber a_k=15000\left[{\frac{tsen(100k\pi t)}{100k\pi}}_{t=-0.01}^{t=0.01}-\int^{0.01}_{-0.01}\frac{sen(100k\pi t)}{100k\pi}dt\right] \end{equation}\]

dado que se cumple que \(sen(-x)=-sen(x)\) y \(cos(-x)=cos(x)\):

\[\begin{equation}\nonumber a_k=15000\left[\frac{cos(100k\pi(0.01))}{\left(100k\pi\right)^2}-\frac{cos(100k\pi(-0.01))}{\left(100k\pi\right)^2}\right]=0 \end{equation}\]

Para los coeficientes \(b_k\) se expresa:

\[\begin{equation}\nonumber b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt=\frac{2}{0.02}\int^{0.01}_{-0.01}150tsen(k\omega_0t)dt \end{equation}\]

\[\begin{equation}\nonumber b_k=-\frac{3}{k\pi}\left[cos(k\pi t)\right],k=1,2,3... \end{equation}\]

El código de MATLAB® que permite calcular la serie trigonométrica de Fourier de la función diente de sierra, considerando los primeros 15 términos de la serie, es decir, con \(n=15\) es el siguiente

n = 15;   
figure
hold on 

x_t =0*t;

for k = 1:n
     bk = -3/(k*pi)*(cos(k*pi));
     x_t = x_t + bk*sin(100*k*pi*t);
end

plot(t,x_t,'k'),grid

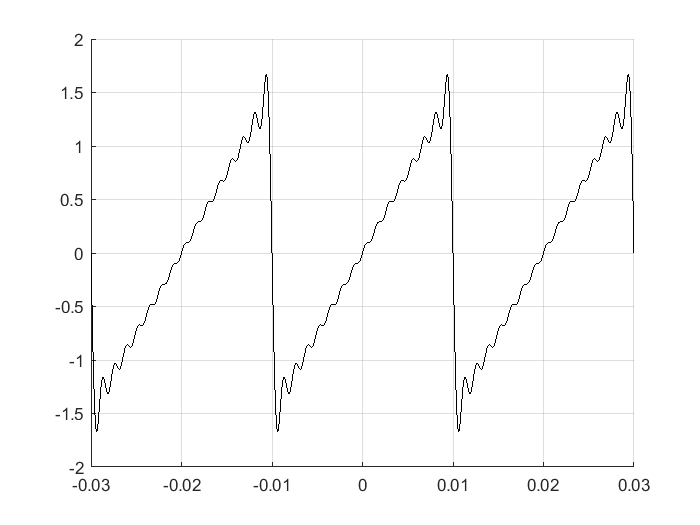
Para comparar \(g(t)\) con su aproximación usando la serie trigonométrica de Fourier se unas las instrucciones siguientes:

figure
plot(t,g);
xlabel("t");
ylabel("g(t)")
axis([-0.03 0.03 -1.8 1.8]) %La istrucción axis ajusta los ejes de la gráfica
grid;
hold on
plot(t,x_t,'k')
legend("Señal diente de sierra","Aproximación con 15 términos")

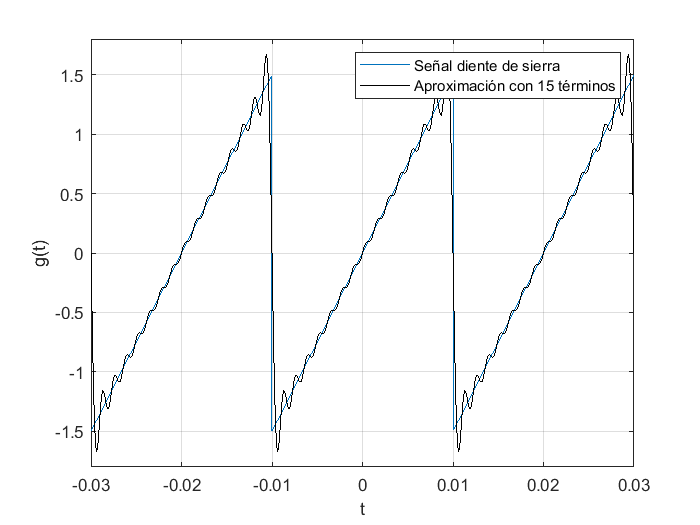
Entre más términos se consideren de la aproximación, es decir, entre mayor sea n en el programa, más parecida será la aproximación, por ejemplo, con \(n=100\):

n = 100;   
figure
hold on 

x_t =0*t;

for k = 1:n
     bk = -3/(k*pi)*(cos(k*pi));
     x_t = x_t + bk*sin(100*k*pi*t);
end

plot(t,x_t,'k'),grid

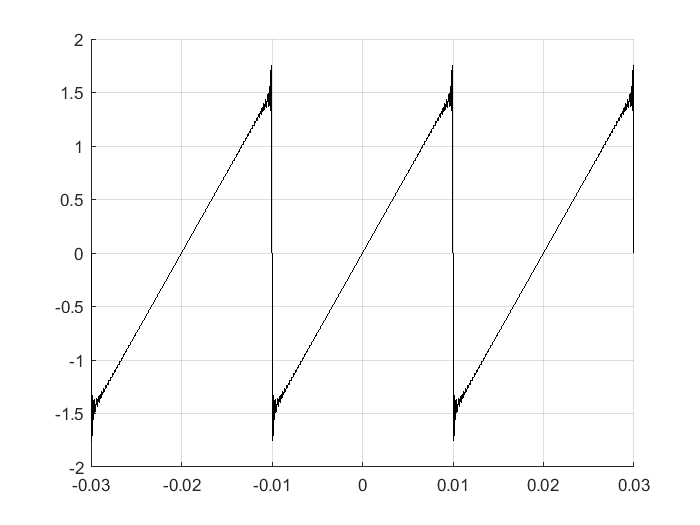
A la distorción en las siscontinuidades o cambios en la señal se le conoce como fenómeno de Gibbs (Kamen and Heck [KH07].)

Ejercicio de la práctica 4

1. Escriba el código de MATLAB® para calcular el resultado de las siguientes sumatorias usando una instrucción de bucle.

• \[ \begin{equation} a=\sum^{100}_{k=1}\left(k-2\right)\left(k^2-4\right) \end {equation} \]
• \[ \begin{equation} b=\sum^{100}_{k=1}\frac{\left(3k-2\right)\left(1-k\right)}{(2k-1)} \end {equation} \]
• \[ \begin{equation} c=\sum^{50}_{j=1}\left(j^3-2j^2-5j\right) \end {equation} \]
• \[ \begin{equation} d=\sum^{100}_{i=1}\sum^{10}_{k=1}\left(5k+4\right)\frac{2i}{\left(3k+2\right)^2} \end {equation} \]

2- Escriba una función para asignar una calificación con una letra de acuerdo con los siguientes criterios:

• \(MB\): muy bien, si la calificación es \(\geq 9.5\) y \(\lt 10\).

• \(B\): bien, si la calificación es \(\geq 8\) y \(\lt 9.5\).

• \(S\): suficiente, si la calificación es \(\geq 6\) y \(\lt 7.9\)

Escriba una función que tenga como entrada una calificación numérica de 0 a 10 y le asigne una calificación literal de acuerdo a los criterios especificados.

Los motores de los cohetes vuelan en tres etapas principales. Una vez que la primera etapa se quema, se separa del fuselaje del cohete y la segunda etapa se enciende. Luego la segunda etapa se quema y separa del fuselaje, y la tercera etapa se enciende. Finalmente, una vez que la tercera etapa se quema, también se separa del cohete. Suponga que los siguientes datos representan aproximadamente los tiempos durante los que cada etapa se quema:

• Etapa 1: 0 a 120 segundos

• Etapa 2: 120 a 190 segundos

• Etapa 3: 190 a 270 segundos

Escriba un programa o función ara determinar si el cohete está en etapa de vuelo 1, etapa de vuelo 2, etapa de vuelo 3 que significa caída libre.