Práctica 3: Sentencias de control#

En las secciones pasadas se trató el tema de la elaboración de secuencias de instrucciones en forma de un archivo de extensión .m para su ejecución repetida sin necesidad de duplicar el trabajo de volverlas a escribir. Por otra parte se desarrollaron funciones para poder invocarlas o reutilizarlas como fórmulas matemáticas destinadas a obtener resultados de manera recurrente, una vez más sin a necesidad de duplicar código.

En esta práctica, analizaremos las secuencias de control. Las secuencias de control permiten al usuario tener un criterio de decisión sobre que conjunto de instrucciones a ejecutar, con base en necesidades o condiciones específicas, en vez de ejecutar todas las instrucciones de manera secuencial.

Las estructuras de repetición se utilizan en ingeniería para realizar procesos que se conocen como iterativos, para poderlas aplicar de una manera eficiente a la solución de problemas, se depende de operadores que relacionan variables para tomar decisiones basadas en su comparación, estas decisiones a menudo sirven para controlar el programa e incluso terminarlo.

Las operaciones de comparación son básicas para lograr el objetivo antes mencionado. La mayoría de los lenguajes de programación usan el variables booleanas, «1» lógico para verdadero (TRUE) y «0» lógico para falso (FALSE). En MATLAB®, cualquier número diferente de cero indica una condición booleana de verdadero.

Por ejemplo, sean dos variables a=5 y b=10, la comparación entre sus valores numéricos se hace en MATLAB® como sigue:

%Primero se declaran las variables
a=5;
b=10;

Después se hace la comparación usando los operadores de comparación nativos de MATLAB\(^{\textregistered}\). La respuesta a la pregunta: ¿Es a menor que b? se responde con la instrucción:

a<b

ans = logical
   1

Mientras que la respuesta a la pregunta: ¿Es a mayor que b? se responde con la instrucción:

a>b

ans = logical
   0

En los resultados anteriores se comprueba que las condiciones de salida son verdadero y falso como respuesta a cada una de las dos preguntas. Las condiciones de comparación se pueden extender fácilmente a variables del tipo arreglo o vector, por ejemplo:

w=[1 2 -3 4 -5];
x=[2 -3 0 5 6];
y=[3 8 -2 1 4];
y>x 
w<y

ans = 1x5 logical array
   1   1   0   0   0

ans = 1x5 logical array
   1   1   1   0   1

Como se observa en los resultados anteriores, el operador de comparación entrega un arreglo con la misma cantidad de localidades que los dos arreglos que estan bajo comparación. Por ejemplo, cuando se compara al arreglo y con el arreglo x, se observa que 3>2, por lo tanto, la primera comparación es verdadera, resultando en un «1» lógico en la primera localidad de la respuesta, mientras que 1<5, resultando un cero en la localidad 4 del arreglo de respuesta.

Es posible combinar las comparaciones con otros operadores lógicos como AND y OR:

(w<x)&(y>x)

ans = 1x5 logical array
   1   0   0   0   0

(w<y)|(x>y)

ans = 1x5 logical array
   1   1   1   1   1

El resultado de la combinación de comparaciones es un arreglo que obedece al criterio establecido por el operador comparación y el relacional lógico, por ejemplo para la instrucción (w<x)&(y>x) sucede de que 1<3 y a la vez 3>2, esto es la localidad uno del arreglo «w» es menor que la localidad uno del arreglo «x» y a la vez se cumple que la localidad uno del arreglo «y» es mayor que la localidad uno del arreglo «x».

Los operadores relacionales son los siguientes:

Tabla 3 Operadores que relacionan variables#

Operador

Función

==

igual que

>=

mayor o igual que

<=

menor igual que

<

menor que

>

mayor que

~=

diferente que

Mientras que los operadores lógicos son:

Tabla 4 Operadores lógicos#

Operador

Función

&

AND (Y lógica)

|

OR (O lógico)

~

NOT (negación lógica)

xor

XOR (or exclusivo)

Búsqueda de elementos en un conjunto de datos que cumplen con cierto criterio#

En MATLAB® existe una instrucción especial denominada find(), esta instrucción especial busca entre los elementos de un arreglo los elementos que cumplen con un criterio especificado en entre paréntesis. Por ejemplo, considere las mediciones de temperatura almacenadas en un arreglo llamado T. una forma de encontrar las temperaturas superiores a 30 grados es la siguiente:

T=[22,28,33,31,24,20,19,28,32,20,33];
find(T>30)

ans = 1×4 double
     3     4     9    11

Como se puede observar, la instrucción find(T) devuelve las localidades en las cuales el valor almacenado es superior a 30. Así, se puede construir un vector que contenga únicamente los datos que cumplen el criterio. El procedimiento las instrucciones de MATLAB® son las siguientes:

T_30=T(find(T>30))

T_30 = 1×4 double
    33    31    32    33

Cuando se trata con arreglos multidimencionales como las matrices, se puede usar la instrucción find() para localizar los valores que cumplan con los criterios, adicionalmente, se pueden almacenar en dos variables la localización de los elementos buscados en forma de filas y columnas. Por ejemplo, suponga que se desea encontrar los elementos mayores a 5 en la matriz \(A\) definida como:

\[\begin{split} \begin{equation} A=\begin{bmatrix} 4 & 12 & 15 & 10\\ 1 & 2 & 3.3 & 4.5\\ 2 & 10 & 2 & 5.5\\ 12 & 7 & 3 & 8 \end{bmatrix} \end{equation} \end{split}\]

Primero se crea la matriz A:

A=[4  12  15 10;1 2 3.3 4.5;2 10 2 5.5;12 7 3 8]

A = 4×4 double
    4.0000   12.0000   15.0000   10.0000
    1.0000    2.0000    3.3000    4.5000
    2.0000   10.0000    2.0000    5.5000
   12.0000    7.0000    3.0000    8.0000

Para encontrar la localización de los elementos mayores a 5 se usa la instrucción o comando find() como sigue:

find(A>5)

ans = 8×1 double
     4
     5
     7
     8
     9
    13
    15
    16

Las localizaciones de las entradas de la matriz que cumplen con el criterio se almacenan en orden simple, no hay información de la fila y columna, en este caso, las localidades se ubican en orden ascendente, observe que el primer elemento que cumple con el criterio de búsqueda (x>5) se encuentra en la primera columna, en la fila cuatro, mientras que el segundo elemento que cumple con el criterio se encuentra en la fila uno y la segunda columna, es decir, el quinto elemento contando desde el elemento de la fila uno columna uno y continuando en orden ascendente. Para obtener la localización de los datos en formato de filas y columnas se usa la instrucción find() antecedida por un par de variables entre corchetes para almacenar los índices:

[i j]=find(A>5)

i = 8×1 double
     4
     1
     3
     4
     1
     1
     3
     4

j = 8×1 double
     1
     2
     2
     2
     3
     4
     4
     4

En el arreglo i se almacena la información del renglón y en el arreglo j se almacena la información de la columna, de manera que se verifica que el elemento o entrada de la matriz \(a_{ij}\) cumple con el criterio de búsqueda, por ejemplo, en el caso que anterior, el elemento A(4,1) es mayor que 5:

A(4,1)

ans = 12

O equivalentemente:

A(i(1),j(1))

ans = 12

Graficación de funciones continuas a pedazos#

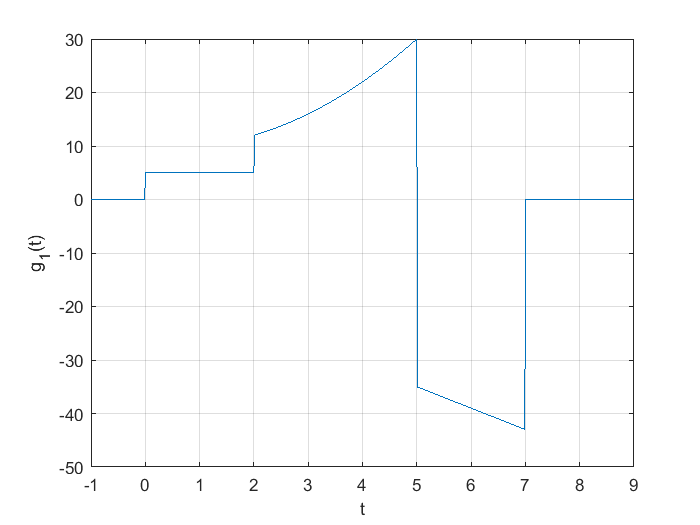
Se dice que una función es definida a pedazos si es continua en un intervalo dado si está definida en un intervalo cualquiera y además, las expresiones matemáticas que describen o modelan a dicha función son continuas en ese intervalo. Adicionalemente, también se cumple que no hay discontinuidad en ningún punto extremo de los subintervalos. Una función continua a pedazos se define por medio de un conjunto de expresiones, utilizando una llave, funciones locales e intervalos. Por ejemplo, considere la función continua a pedazos definida en la siguiente expresión:

(5)#\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} 5 & si & 0 \leq t \leq 2 \\ \\ t^2-t+10 & si & 2 < t \leq 5 \\ \\ -4t-15 & si & 5 < t < 7 \\ \\ 0 & si & 7 \leq t \end{array} \right. \end{equation}\end{split}\]

Como puede observarse, los subintervalos se pueden definir en MATLAB®, usando los comandos de la Tabla 3

t=[-1:0.01:9];
g1=5.*((t>=0)&(t<=2))+(t.^2-t+10).*((t>2)&(t<=5))+(-4*t-15).*((t>5)&(t<7))+0.*(t>=7);

plot(t,g1);
xlabel("t");
ylabel("g_{1}(t)")
grid;
_images/a027ede62cb64f524dcc0283719139b518374f36b21f97e40d04004180f3f04d.png

Atención

Los intervalos se describen como cerrados o abiertos:

  • \([a,b]\) implica un intervalo cerrado y se lee como: «el conjunto de los valores de \(x\) en los números reales tales que \(x\) es mayor o igual que \(a\) y \(x\) es menor o igual que \(b\). En notación matemática se escribe: \(\left\{x\in R| a \leq x \leq b\right\}\)

  • \((a,b)\) implica un intervalo abierto y se lee como: «el conjunto de los valores de \(x\) en los números reales tales que \(x\) es mayor que \(a\) y \(x\) es menor que \(b\). En notación matemática se escribe: \(\left\{x\in R| a < x < b\right\}\)

También son posibles las combinaciones:

  • \([a,b)\) implica un intervalo cerrado y se lee como: «el conjunto de los valores de \(x\) en los números reales tales que \(x\) es mayor o igual que \(a\) y \(x\) es menor que \(b\). En notación matemática se escribe: \(\left\{x\in R| a \leq x < b\right\}\)

  • \((a,b]\) implica un intervalo abierto y se lee como: «el conjunto de los valores de \(x\) en los números reales tales que \(x\) es mayor que \(a\) y \(x\) es menor o igual que \(b\). En notación matemática se escribe: \(\left\{x\in R| a < x \leq b\right\}\)

Ejercicio de la práctica 3#

1.- Dibuje la gráfica de la función definida como:

\[\begin{split} \begin{equation} y(t)= \left\{ \begin{array}{lcc} 0.5t & si & 0 \leq t \leq 2 \\ \\ -2(t-3) & si & 2 < t \leq 5 \\ \\ 1.5(t-6) & si & 5 < t < 7 \\ \\ 0 & si & 7 \leq t \end{array} \right. \end{equation} \end{split}\]

2.- Encuentre para cada uno de los arreglos:

\[\begin{split} \begin{equation} \nonumber \begin{bmatrix} \ 10&25&-3&56\\ \ -43&5&-3&55\\ \ 32&85&-32&26\\ \ -25&45&-52&68 \end{bmatrix}~~\begin{bmatrix} \ 34&-53&32&-15\\ \end{bmatrix}~~ \begin{bmatrix} \ 12.3&15.4&-30.8\\ \ -4.3&15.1&3.5\\ \ 33.45&85.4&13.0 \end{bmatrix} \end{equation} \end{split}\]

Las localidades de los elementos que cumplan con lo siguiente:

  • Los elementos o localidades positivas: \(a_{ij}\geq 0\)

  • Los elementos o localidades mayores a \(12\) y menores a \(35\)

  • Los elementos o localidades en el intervalo \(\left[15,40\right]\)

  • Los elementos o localidades en el intervalo \(\left(-10,90\right)\)

  • Los elementos o localidades en el intervalo \(\left[10,30\right)\)