Práctica 5: Entrada-salida de datos y formatos de despliegue

En esta prácitca se abordan situaciones que se presentan cuando se trabaja con programas, cuyo objetivo o aplicación final implican que el programador y el usuario final del código pudieran ser personas diferentes. Esto hará necesaria una comunicación sencilla y efectiva con el usuario a través de instrucciones y funciones de entrada y salid. Como se vio en la Práctica 2, en MATLAB® existen funciones nativas que permiten al usuario comunicarse con un programa conforme se ejecuta. El comando input() permite solicitar al usuario el valor de un dato de entrada y almacenarlo para su posterior uso. Las funciones nativas disp() y fprintf() porporcionan una salida visual en la ventana de comandos.

La función input() permite ingresar incluso arreglos completos, por ejemplom si se usa la instrucción:

>>v=input("ingese un vector con el formato de corchetes")

El usuario introduce el vector en formato de corchetes:

>>[1,-3,5];

Tambien se puede introducir una matriz completa:

A=input("ingese una matriz cuadrada con el formato de corchetes")

El usuario introdude la Matriz A en formato de corchetes:

>>[1 3 4;5 6 -1;9 2 5]

Una consideración importante es el hecho de que los datos de entrada tambien puenden ser cadenas de caracteres o texto:

>>nombre=input("ingese su nombre completo entre comillas")

El usuario entonces puede introducir su nombre usando el formato de las comillas:

>>"Luis Gerardo Trujillo Franco"

Recolección de puntos de una gráfica

Una opción más para solicitar datos de entrada al usuario, es por medio de la coleción de datos directamente de una curva en una gráfica. Esta forma de solicitar datos al usuario se lleva a cabo usado la función ginput(). Esta función se utiliza para colectar puntos en forma de pares ordenados, el número entre paréntesis es el total de puntos o pares ordenados que se colectarán de la gráfica. Lo anterior se muestra en el siguiente video:

Las siguientes instrucciones permiten reproducir lo mostrado en el video:

t=[0:0.001:2];
y=exp(-3.5*t).*cos(45.*t);

Usando el comado ginput se otienen, por ejemplo, las coordenadas de dos crestas de la gráfica:

plot(t,y)
[x,y]=ginput(2)

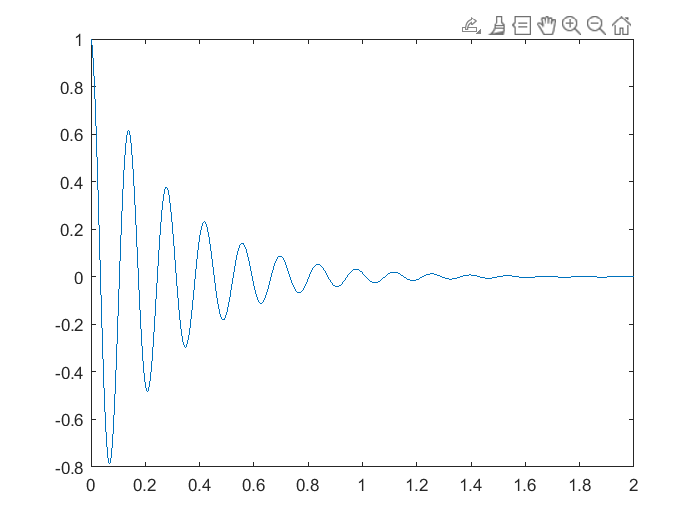
x = 2×1 double
    0.1381
    0.2228

y = 2×1 double
    0.6110
   -0.4867

La función menú como entrada de datos

Una opción interactiva es la que ofrece la función interna menu, cuya sintaxis se muestra a continuación: ``entrada=menu(«Mensaje al usuario»,»Texto para el botón 1»,»Texto para el botón 2»,…,»Texto para el botón n»). La salida, que se almacena en la variable entrada, es un número entero que depende del botón sobre el cual se hizo click, por ejemplo si se presiona el botón rotulado con el mensaje opción 1 la salida enttrada será igual a uno como se muestra en el siguiente clip y en el código de salida de abajo.

entrada=menu("Seleccione una opción","Opción 1","Opción2","Opción 3")

entrada = 2

Un ejemplo simple de aplicación de la función menu es el siguiente programa, el cual proporciona el peso específico del material que se muestra en el menu:

% Programa de ejemplo de aplicación de la función menú
% Fuente: https://concepto.de/peso-especifico/#ixzz8V4bEJMuH

material=menu("Selecione el material","Acero","Aluminio","Bronce","Plomo","Zinc")

switch material

       case 1
          disp("7850 N/m3")
       case 2
          disp("2700 N/m3")
       case 3
          disp("8600 N/m3")
       case 4
          disp("11400 N/m3")
       case 5
          disp("7200 N/m3")
end

material = 2

2700 N/m3

Formatos de salida de datos

En MATLAB®, la función fprintf() (función impresión formateada) proporciona un mayor control sobre la salida de la que tiene con la función disp(). Además de desplegar valores tanto texto como arreglos, puede especificar el formato requerido para desplegar los valores, y puede especificar también un cambio de línea. La forma general de la función nativa fprintf() contiene dos argumentos, uno tipo texto o cadena de caracteres y otro una lista de variables en forma de constantes o matrices, según se requiera: fprintf("Texto de formato",variable 1, variable 2,...,variable n). Un ejemplo se muestra abajo:

metales=5;
polimeros=3;
ceramicos=14;

fprintf("Hay %f metales, %f polímeros y %f cerámicos",metales,polimeros,ceramicos)

Hay 5.000000 metales, 3.000000 polímeros y 14.000000 cerámicos

Nótese como es necesario incluir un especificador %f, por cada número que se desea desplegar. En el caso anterior, resulta más conveniente mostrar las cantidades de materiales como enteros, para ello se utiliza la especificación de formato %d.

metales=5;
polimeros=3;
ceramicos=14;

fprintf("Hay %d metales, %d polímeros y %d cerámicos",metales,polimeros,ceramicos)

Hay 5 metales, 3 polímeros y 14 cerámicos

La siguiente tabla resume algunos de los formatos de datos más utilizados para representar información en MATLAB®:

Tabla 5 Tabla de formatos para despliegue de información.

Tipo de formato	Dato o notación resultante
%f	Notación de numeros decimales
%e	Notación exponencial (7.8e3=7800)
%g	Usará la notación que resulte más corta %f o %e
%c	Notación para caracteres
%d	Notación para enteros
%s	Notación para texto o cadena de caracteres

También es posible usar comandos de formato especial, por ejemplo, el tabulador \t es muy útil para crear tablas en las cuales las línesa se ajusten de manera ordenada. Es posible ontrolar aún más cómo se despliegan las variables al usar especificaciones como width field y precision field con el comando format, width field controla el número mínimo de caracteres a imprimir. Debe ser un entero positivo. El precision field está precedido por un punto (.) y especifica el número de decimales después del punto decimal para tipos exponencial y punto fijo. Por ejemplo, %5.3f especifica que el ancho total mínimo disponible para desplegar su resultado es cinco dígitos, de los cuales, tres están después del punto decimal. Por ejemplo:

presion=4.5;
fprintf("La presión es %5.3f kilo Pascales \n",presion)

La presión es 4.500 kilo Pascales 

El espacio vacío entre el texto y el número 4.500 se debe a que se reservan, por la indicación de formato %5.3f se reservaron 2 espacios para la parte entera del número a desplegar. El comando o función fprintf() tambíen se exptiende a cada uno de los elementos de los arreglos. Por ejemplo para una tabla de centímetros y pulgadas se puede usar el siguiente código:

% Tabla de conversión de centímetros a pulgadas
cm=[1:0.5:5];
pulgadas=cm./2.54;
tabla=[cm;pulgadas]; % Se agrupan los datos convertidos en una matriz que será la tabla de datos
disp("  Cm   Pulg")
fprintf("%6.3f %6.3f \n",tabla)

  Cm   Pulg
 1.000  0.394 
 1.500  0.591 
 2.000  0.787 
 2.500  0.984 
 3.000  1.181 
 3.500  1.378 
 4.000  1.575 
 4.500  1.772 
 5.000  1.969 

Una tabla con comandos de formato especial es la siguiente:

Tabla 6 Tabla de formatos especiales.

Tipo de formato	Acción de formato resultante
\n	Salto de línea
\r	Regreso de carro
\t	Tabulador
\b	Retroceder un espacio

Ejercicio de la práctica 5.

Escriba un programa que despliegue un menú con 4 opciones que realice las siguientes funciones según la selección del usuario.

1.- Grafica la parábola \(y=3(x-2)^2\) en el intervalo \([-10,10]\).

2.- Hace el cálculo de: \(z=\sqrt{\frac{354+45}{2}}\).

3.- Grafica \(y=5x^3-2x^2+3x+2\) en el intervalo \([-15.15]\) y solicita al usuario 4 puntos de la gráfica.

4.- Suma los primeros 150 enteros.

5.- Use el comando disp para crear un título para una tabla que convierta centímetros a pies.

6.- Use el comando disp para crear encabezados de columna para la tabla anterior.

7.- Cree un vector de centímetros desde 30 hasta 1200 con un incremento de 100. Calcule los correspondientes valores de pies. Agrupe el vector cm y el vector pies en una matriz tabla. Use el comando fprintf para enviar la tabla a la ventana de comandos para visualizarla.