Práctica 6: Matrices y su manejo#
Las entradas o elementos de las matrices se definen ingresando conjuntos de datos entre los simbolos «[» y «]». Para crear una matriz en MATLAB® se separa cada elemento con un espacio o coma de forma indistinta como hemos visto en prácticas anteriores. Las siguientes instucciones para la creación de matrices en MATLAB® son equivalentes:
C=[1.3]
B=[1 -3 4]
B=[1,-3,4]
A=[-1 3;3 -4]
A=[-1,3;3,-4]
C = 1.3000
B =
1 -3 4
B =
1 -3 4
A =
-1 3
3 -4
A =
-1 3
3 -4
Es posible además, usar un formato que resulta más compatible con la notación matemática como se muestra en la siguiente línea de código:
A=[-1 3 4;
5 3 6;
3 -4 8]
A =
-1 3 4
5 3 6
3 -4 8
Alternativamente, se puede evitar el uso de punto y coma, usando la siguiente sintaxis:
A=[-1,3,4
5,3,6
3,-4,8]
A =
-1 3 4
5 3 6
3 -4 8
Las matrices columna, son las que comnmente conocemos como vectores, su creación se consigue con la instrucción:
V=[1;3;5]
V =
1
3
5
Haciendo uso del operador elipsis (…) es posible reducir el espacio horizontal necesario para la construcción de un areglo o vector de grandes dimensiones o gran cantidad de datos de entrada.
R=[11,43,54,65,67,79,34,89,55,43,78]
disp("Usando la elipsis tres puntos:")
R=[11,43,54,65,67,...
79,34,89,55,43,78]
R =
11 43 54 65 67 79 34 89 55 43 78
Usando la elipsis tres puntos:
R =
11 43 54 65 67 79 34 89 55 43 78
Otra característica muy útil de MATLAB® es la posibilidad de concatenar o combinar matrices para crear otra más grande, por ejemplo, si se tienen dos matrices \(X\) y \(Y\), se puede crear una matriz \(Z\) que sea el resultado de combinarlas:
La matriz \(Z\) se puede crear entonces como:
En MATLAB®, el código para la creación de la matriz \(Z\), resultado de la combinación de las matrices \(X\) y \(Y\) es:
X=[3 2 -5]
Y=[-3 22 -15 34 -16]
disp("Matriz Z=[X Y]")
Z=[X Y]
X =
3 2 -5
Y =
-3 22 -15 34 -16
Matriz Z=[X Y]
Z =
3 2 -5 -3 22 -15 34 -16
La función de concatenación de matrices es especialmente útil cuando se realiza una adquisición de datos o se genera una función que se actualiza o aumenta de tamaño y se requiere almacenar la información en un arreglo para post-procesamiento y/ó graficación. Otra función importante que permite MATLAB® cuando se trabaja con matrices, es la asignación o cambio de valores de los elementos. Como ya se hizo en las primeras prácticas, se puede accesar a un elemento de una matriz por medio de la indexación. Para cambiar o asignar un valor requerido a un elemento en particular de una matriz se usa la sintaxis siguiente:
A=[-4 3 4 5 8];
A(2)=-1
A =
-4 -1 4 5 8
Como puede notarse, el valor del elemento 2 del arreglo A, fué asignado originalmente como 3, por medio de la instrucción A(2)=-1, se asigna un valor de -1 a esa localidad. Se puede extender el tamaño de la matriz original si se asiga un valor a nuevos elementos que no estaban presentes en el arreglo original, por ejemplo:
A(6)=13
A =
-4 -1 4 5 8 13
El Arreglo o matriz A, ha aumentado una localidad en tamaño, es decir, se ha realizado la concatenación de un solo valor a la matriz en vez de concatenar varios valores a la vez. Si la localidad supera aun más el tamaño del arreglo, MATLAB® rellenará con ceros las localidades no asignadas:
A=[-4 3 4 5 8];
A(8)=-3
A(10)=5
A =
-4 3 4 5 8 0 0 -3
A =
-4 3 4 5 8 0 0 -3 0 5
El operador :#
El operador : es muy útil para crear vectores que contengan un rango de valores de alguna variable independiente, esto es muy útil para graficar una función del tipo \(y=f(x)\) en un intervalo o dominio específico. El operador dos puntos es un operador muy poderoso para definir finir una matriz igualmente espaciadas, es decir, con un incremento fijo. por ejemplo, sea la curva \(y=5x^4-4x^3+3x^2-6x+2\), la gráfica de la funcíon evaluada en el intervalo \(-2 \leq x \leq 2\) se obitiene en MATLAB® con las intrucciones:
x=[-2:0.1:2];%Intervalo o dominio de interés
y=-0.5*x.^4+24*x.^3-13*x.^2+6*x-12;
% Se grafica la curva con el comando plot()
plot(x,y)
title("f(x)=-0.5x^4+24x^3-13x^2+6x-12")
xlabel("x")
ylabel("y=f(x)")
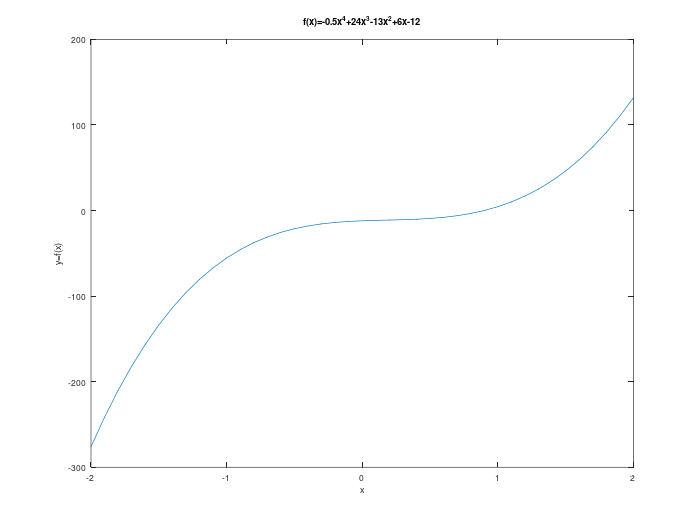
Por defecto, el incremento es unitario, es decir, de no especificarse, MATLAB® creará una matriz con números que difieren exactamete en uno:
t=[0:7]
t =
0 1 2 3 4 5 6 7
El operador : permite incluso aislar las entradas o localidades los arreglos en general. De manera equivalente, se puede decir que esta función de MATLAB® permite la cosntrucción de sub-arreglos o sub-matrices. Por ejemplo, sea la matriz \(A\) definida como:
Se puede extraer la columna 2 de la matriz A con las siguientes instrucciones:
A=[ 11 -23 -4.5 3.8;
-3 14 66 -12;
-51 81 104 0.67;
-4 3 7 -9];
c=A(:,2)
c =
-23
14
81
3
La operación anterior se interpreta de la siguiente manera: extrae “todas las filas en la columna 2”. Para extraer
una fila en específico se usa la sintaxis d=A(2,:), que significa; extrae todas las columnas de la fila 2.
d=A(2,:)
d =
-3 14 66 -12
Es posible extraer parte de una fila o una columna sin extraerla toda completa. El operador : puntos también se puede usar para especificar una extracción de localidades “desde fila i hasta fila k” o “desde columna l hasta columna m”. Por ejemplo, para extraer las dos filas superiores de la matriz A, se escribe:
s=A(1:2,:)
s =
11.0000 -23.0000 -4.5000 3.8000
-3.0000 14.0000 66.0000 -12.0000
La instrucción anterior se interpreta como “filas 1 a 2, todas las columnas”. De manera similar, para extraer sólo los cuatro números en la esquina inferior derecha de la matriz A se escribe:
i=A(3:4,3:4)
i =
104.0000 0.6700
7.0000 -9.0000
Es posible crear una matriz vacía para posteriormente asignar valores a sus localidades, por ejemplo para crear una matriz que contenga todos los números en órden del 1 al 16 se usa el siguiente conjunto de instrucciones:
clear
clc
close all
A=[];% se crea una matriz vacía
r=0;
for i=1:4
for j=1:4
r=r+1;
A(i,j)=r;
end
end
A
A =
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
Como ya se ha mencionado en prácticas anteriores, para acceder a una localidad o entrada en una matriz se especifica entre paréntesis el número de fila y el número de columna separados por una coma, por ejemplo para accesar a la localidad o entrada \(A(3,2)\) se escribe:
elemento=A(3,2) %La variable elemento almacena la entrada A(3,2) de la matriz A
elemento = 10
De manera alternativa, puede usar un solo número índice. El valor en la fila 3, columna 2 de la matriz A es el elemento número 7. (Se cuenta la columna 1, luego la columna 2, hasta el elemento correcto.) El comando MATLAB® asociado es:
elemento=A(7)
elemento = 10
Ejercicio de la práctica 6.#
Construya los siguientes arreglos:
Una vez creadas las matrices o arreglos , resuelva los siguientes ejercicios:
1.- Extraiga y almacene en una variable \(v_1\) el elemento \(w_{1,3}\).
2.- Extraiga y almacene en un arreglo \(v_2\) la primera fila de la matriz \(x\).
3.- Extraiga y almacene en un arreglo \(v_3\) la segunda columna de la matriz \(x\).
4.- Asigne a la variable \(z\) los valores en la matriz \(x\) a lo largo de la diagonal principal.
5.- Construya una matriz \(r\) tal que los primeros cuatro valores en la matriz \(w\) sean su primera fila y las localidades en la matriz \(x\) como el resto de columnas y filas.
6.- Asigne a la variable \(t\) los valores en la matriz \(y\) como la primera columna, los valores en la matriz \(x\) como las columnas 2, 3, 4 y 5, y los valores en la matriz \(w\) como la última fila.
7.- Asigne a la variable \(a\) el valor del elemento 7 en la matriz \(x\), aplicando la asignación de índice simple.
8.- Construya un arreglo \(G\) tal que almacene el resultado de convertir al arreglo o matriz \(x\) en un vector tipo columna.
