Práctica 9: Graficación

Las gráficas son una herramienta básica del ingeniero y del cientifico en general, dada su utilidad para representar datos de forma visual y la oportunidad que ofrecen para interpretar la relación etre pares o triadas de variables o bien, la evolución en el tiempo de las variables de interés. En este curso hemos escrito el código para generar gráficas y hemos comprobado su utilidad para el desarrollo de la ingeniería. En esta práctica trataremos con algunos aspectos importantes de la graficación de datos haciendo uso de MATLAB® para complementar y mejorar la presentación de las gráficas.

Gráficas de funciones de una variable

Una aplicación clásica de las gráficas en la ingeniería es la graficación de funciones en las asignaturas de cálculo diferencial e integral. La definición de función clásica involucra a una variable independiente y una transformación numérica que genera una nueva variable, matemáticamente se expresa como \(y=f(x)\), donde \(f(x)\) tiene muy variadas estructuras, desde la recta \(f(x)=mx+b\), hasta la combinación de funciones exponenciales y trigonométricas \(f(x)=e^{-3x}cos(2\pi x+\phi)\).

En ingeniería, es común que las gráficas se generen a partir de tablas de datos que se construyen a partir de conjuntos ordenados de variables que constituyen los puntos de la gráfica. Las gráficas resultan ser entonces reprecentaciones de la interacción o correlación entre dos variables de algún proceso o fenómeno.

Por ejemplo, en un experimento se obtienen los puntos que relacionan la deformación y la fuerza medida por un dinamómetro, para el caso de un resorte no lineal, se almacenan los datos en dos columnas principales, una con las deformaciones del resorte y una más con la fuerza registrada por un dinamómetro. La gráfica de los datos mostrará la relación entre ambas variables. Una gráfica de fuerza contra deformación se realiza fácilmente a partir de los datos experimentales mostrados en la Tabla 10.

Tabla 10 Tabla de datos experimentales de un resorte cúbico.

\(\Delta x\)	\(F~[N]\)
0	0
0.0100	0.0252
0.0201	0.0123
0.0301	0.0283
0.0402	0.0745
0.0502	0.1305
0.0602	0.2484
0.0703	0.3573
0.0803	0.5369
0.0904	0.7420

Las instrucciones para graficar los puntos de la tabla de datos experimentales se generan los vectores con los dtos a graficar y se usa el comando plot() como en practicas anteriores, con la diferencia de que en esta ocasión se graficarán los puntos o pares ordenados, usando asteríscos en vez de una línea contínua:

clear
close all
delta_exp=[0 0.01 0.0201 0.0301 0.0402 0.0502 0.0602 0.0703 0.0803 0.0904];
F_exp=[0 0.0252 0.0123 0.0283 0.0745 0.1305 0.2484 0.3573 0.5369 0.742];
plot(delta_exp,F_exp,'*')

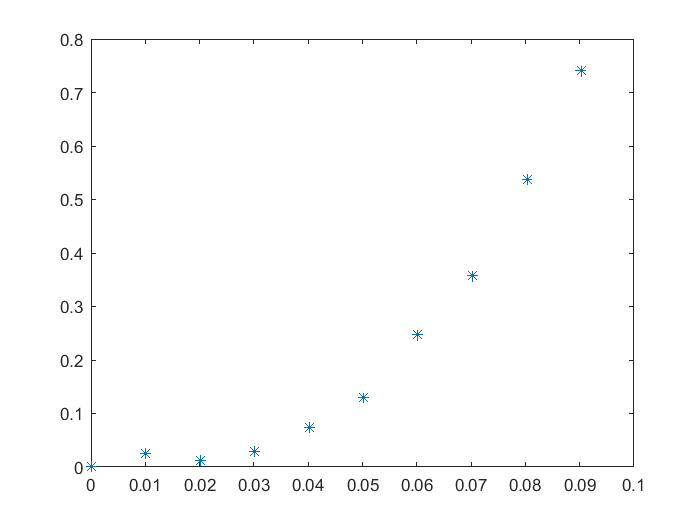
Para anexar un título a la gráfica anterior se usa el comando title() con el rótulo deseado dentro del paréntesis y entre comillas.

title("Curva Fuerza vs deformación")

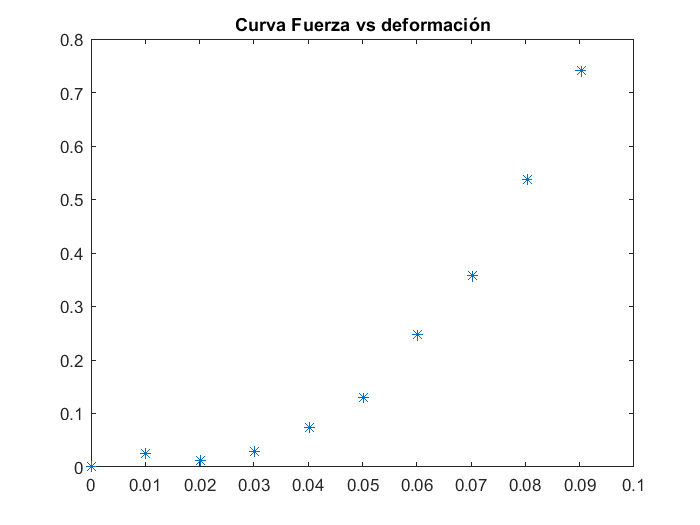
los rótulos para los ejes se escriben usado los comandos xlabel() y ylabel() para los ejes horizontal y veritical respectivamente:

xlabel("Deformación [m]")
ylabel("Fuerza [N]")

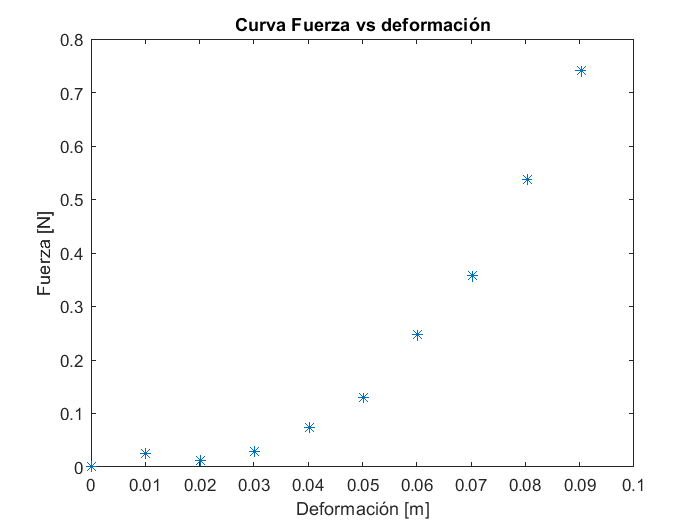
Se puede activar una cuadrícula para una mejor lectura e interpretación de los datos de la gráfica usando el comando grid o grid on.

grid

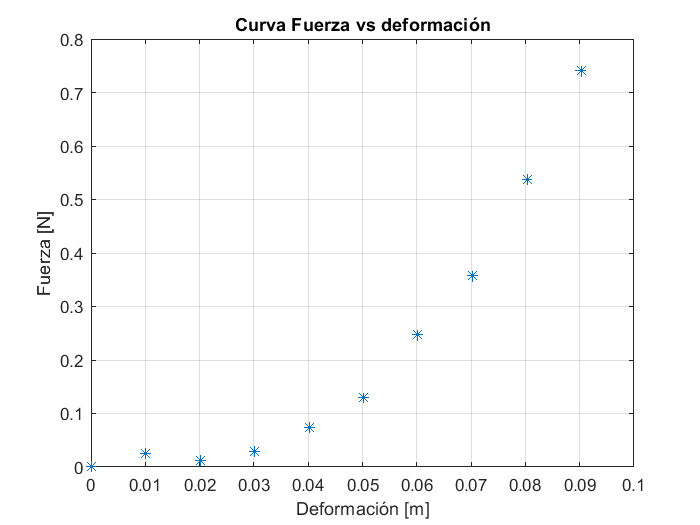
Es importante tomar en cuenta que todos los comandos anteriores surten efecto mientras la gráfica esté abierta, una vez cerrada la imagen con la gráfica se perderán los datos graficados y solo aparecerá un título, cuadrícula o rótulo para el eje x o y sin ningun dato graficado.

Tabla 11 Tabla de formatos para una gráfica en MATLAB®.

Tipo de línea	Caracter	Tipo de punto	Caracter	Color de línea	Caracter
Contínua/sólida	-	Punto	.	Azul	b
Punteada	:	Círculo	⁰	verde	g
Raya-punto	-.	marca x	x	rojo	r
Línea discontínua	--	signo +	+	cian	c
		estrella	*	magenta	m
		cuadrado	s	amarillo	y
		diamante	d	negro	k
		triangulo arriba	^	blanco	w
		triangulo izquierda	<
		triangulo derecha	>
		pentagrama	p
		hexagrama	h

Para hacer uso de los datos en un archivo es necesario cargarlos o importarlos al workspace de MATLAB®, la importación de los datos se lleva a cabo usando la instrucción load(), el argumento de entrada es el nombre del archivo en el que se encuentran los datos. Para el caso de datos que se encuentran en internet, se utiliza el comando readtable() tal y como se hizo en la práctica 7. Una operación común que se hace cuando se grafican datos es mostrarlos en una misma figura, tal y como se mostró en la práctica 7, la instrucción hold on perrmite realizar esta operación como a continuación se ejemplifica:

clear
close all
x=[-pi:0.01:pi];
y=sin(x);
w=cos(4*x);

plot(x,y,"b")
hold on 
plot(x,w,"r")
grid

xlabel("x")
ylabel("y=f(x)")
title("Gráfica de y(x) y w(x)")

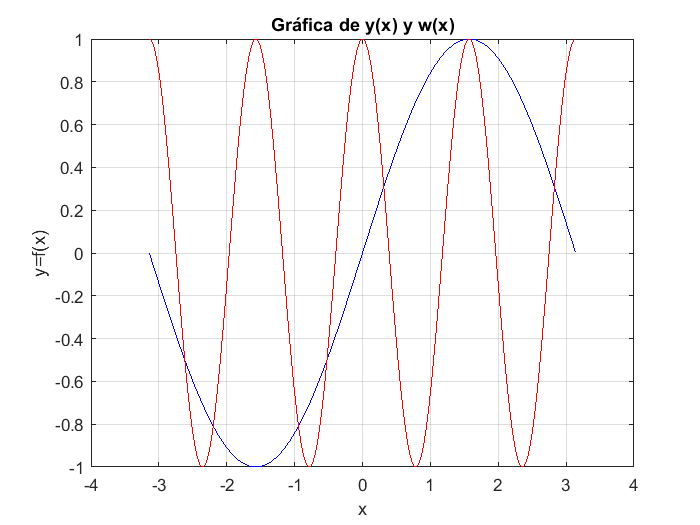
Para hacer una señalización del significado de cada curva graficada, es decir, para identificar cada una de las funciones graficadas, se anexa un rótulo o etiquetas. Los rótulos son acompañados por un segmento de recta del color de cada curva de datos para poder distinguir la pertnenecia a cada curva. Para añadir este rótulo distintivo se utiliza el comando legend() en el cual, se escribe entre paréntesis y etrecomillado el rótulo distintivo de cada función, curva o par de datos.

legend("sen(x)","cos(4x)")

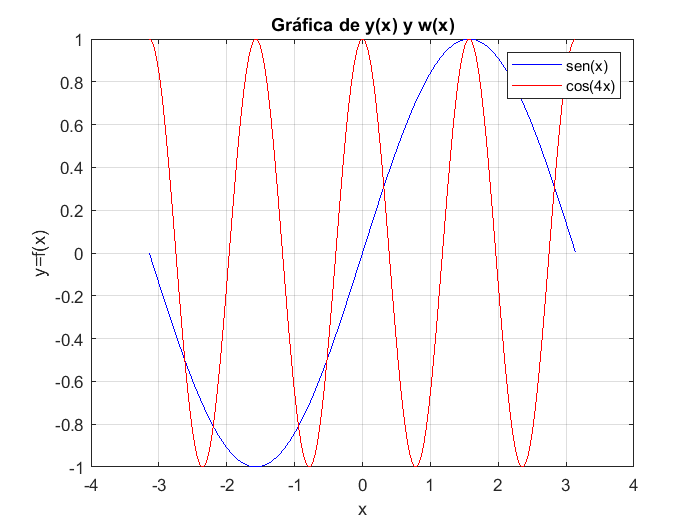
Tambien se puede ajustar el rango de visualización en los ejes horizontal y vertical, esto se logra haciedo uso del comado axis(), el cual recibe como argumento un vector o arreglo con los valores máximos y mínimos de los ejes, es decir ´[xmin,xmax,ymin,ymax]´. Para ejemplificar esto, manipularemos los rangos de los ejes de la gráfica que hemos venido trabajando, para especificar la visualización de las gráficas de las funciones \(y=sin(x)\) y \(w=cos(4x)\) en los intervalos \(-2<x<2\) y \(-0.5<y<0.5\) se usan los comandos:

axis([-2,2,-0.5,0.5])

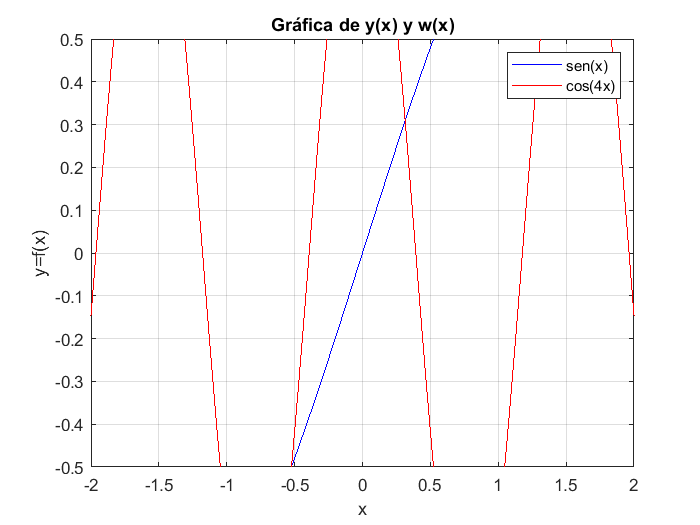
Graficas en tres dimensiones

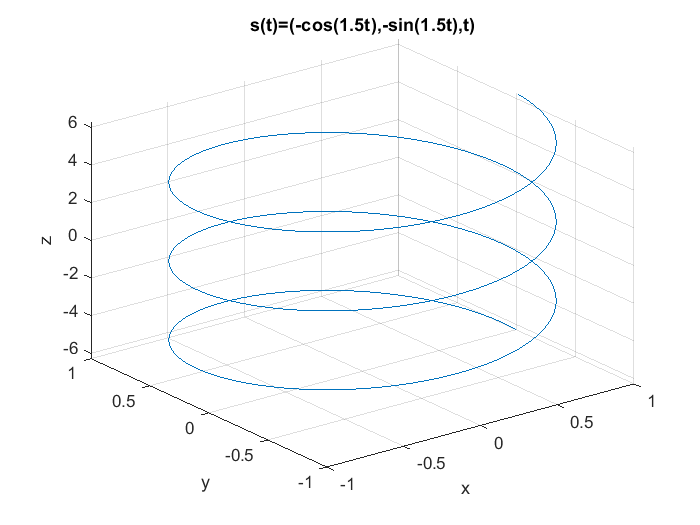
La instrucción plot() genera gráficas de dos variables en una figura, es decir, genera gráficas con dos coordenadas, En ingeniería es común el uso de gráficas de tres dimensiones o bien el graficar curvas en el espacio \(\mathbb{R}^3\), la instrucción o comando para generar una gráfica tridimensional es plot3(), la cual tiene por argumentos tres arreglos o vectores correspondientes a los datos a graficar por cada eje, por ejemplo sea la hélice definida como:

\[\begin{split} \begin{eqnarray} x=&-cos(1.5t)\\ y=&-sen(1.5t)\\ z=&t \end{eqnarray} \end{split}\]

con \(2\pi<t<2\pi\)

la gráfica de la hélice se lleva a cabo en MATLAB® usando los siguientes comandos:

clear 
close all
clc
t=[-2*pi:0.01:2*pi];
x=-cos(1.5*t);
y=-sin(1.5*t);
z=t;

plot3(x,y,z)
title("s(t)=(-cos(1.5t),-sin(1.5t),t)")
grid

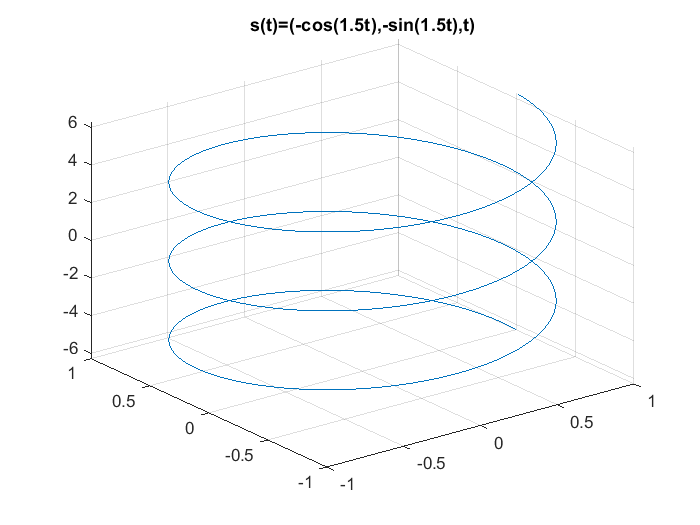
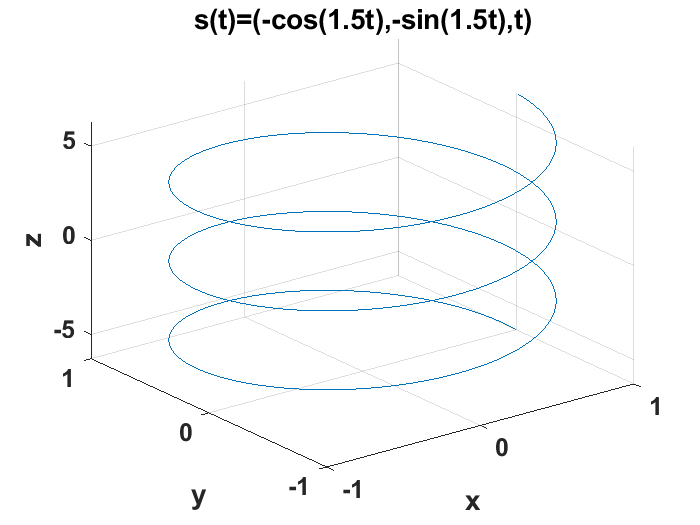
Es posible asignar rótulos a cada uno de los ejes como en el caso de las gráficas de dos dimenciones, usando los comandos xlabel(), ylabel() y zlabel(), además del título y la cuadrícula correspondiente:

xlabel("x")
ylabel("y")
zlabel("z")

Para especificar un tipo y tamaño de letra en una figura o gráfica se usan las isntrucciónes:

set(gca,'fontsize',15);
set(gca,'fontname','Arial','FontWeight','Bold');

Tabla 12 Tabla de instrucciones de graficación.

Comando MATLAB®	Descripción	Sintaxis
figure	Genera una figura nueva o vacía para una o varias gráficas	figure
plot	Grafica un par de vectores o arreglos de datos y contra x	plot(x,y)
title	Adiciona un título a una gráfica	title("Título de la gráfica")
xlabel	Agrega un rótulo al eje horizontal	xlabel("Rótulo del eje x")
ylabel	Agrega un rótulo al eje vertical	ylabel("Rótulo del eje y")
grid	Agrega una cuadrícula a la gráfica	grid
hold on	Activa la opción de trazar dos curvas diferentes en una misma gráfica	hold on activa la opción hold off desactiva la opción.
axis(v)	Ajusta el rango de los ejes para una mejor visualización	axis(v) la entrada v es un vector de cuatro elementos: [xmin,xmax,ymin,ymax]
legend()	Agrega una leyenda o rótulo a la gráfica para distinguir las curvas en una misma gráfica.	legend("rótulo 1","rótulo 2",etc)
set(gca,”fontsize”,n)	Establece el tamaño de letra en la gráfica.	set(gca,'fontsize',n) n es el tamaño de letra deseado
set(gca,…,…,…,…)	Establece el tipo y estilo de letra en la gráfica.	set(gca,'fontname','Arial','FontWeight','Bold')

Gráficas múltiples en una misma figura

Es posible generar multiples ejes coordenados en una misma figura para trazar curvas independientes si la necesidad de que compertan una misma gráfica. Esta división de gráficas se consigue haciendo uso del comando subplot(i,j,n), donde i es el número de renglón, j el número de columna y n el número de gráfica o curva a dibujar, por ejemplo para generar dos gráficas, en dos diferentes ejes coordenados, en dos columnas y en una misma figura se usan las siguientes instrucciones:

clear 
close all
clc
x=[-pi:0.01:pi];
y=2*sin(3*x)+2;
w=2*cos(4*x)-2;

figure
subplot(1,2,1)
plot(x,y)

subplot(1,2,2)
plot(x,w)

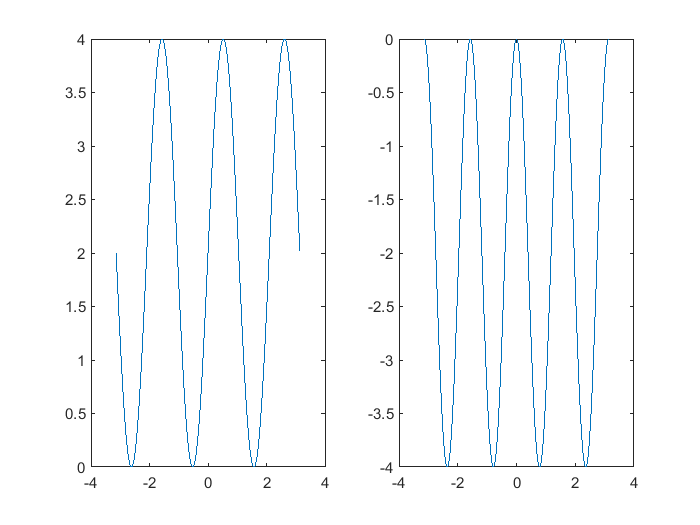
Las mismas instrucciones que se se utilizan para modificar las gráficas en una figura simple se pueden utilizar para modificar las gráficas múltiples, siempre y cuando se escriban en un mismo contexto de tipo subplot como se muestra a continuación:

clear 
close all
clc
x=[-pi:0.01:pi];
y=2*sin(3*x)+2;
w=2*cos(4*x)-2;

figure
subplot(1,2,1) %Conjunto de gráficas en una misma figura de una fila, dos columnas
plot(x,y,'r--')
title("y=f(x)")
xlabel("x")
ylabel("y")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold');

subplot(1,2,2) %Segunda gráfica en la segunda columna primera fila
plot(x,w,"m+")
title("w=f(t)")
xlabel("t")
ylabel("w")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Arial','FontWeight','Bold');

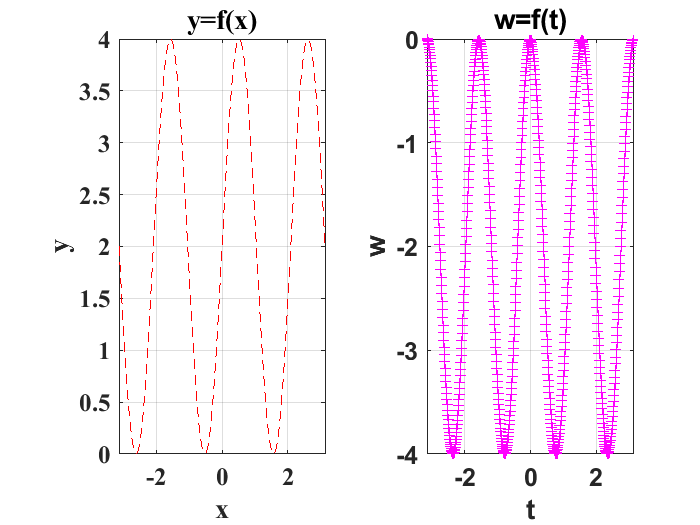
Tambien se pueden combinar gráficas tridimencionales con curvas en el plano en una misma figura. Para ilustrar esto, haremos la gráfica de las siguientes funciones en una misma figura:

\[\begin{split} \begin{eqnarray} &f(x)=(x-2)^2-3\\ &g(t)=(-cos(t),sen(t),t)\\ &h(x)=sen(2x)cos(3x)+4\\ &j(x,y,z)=sen(x)+cos(x)+sen(2x)cos(y) \end{eqnarray} \end{split}\]

Se usará una figura con cuatro subgráficas para generar las cuatro curvas \(f(x)\), \(g(x,y,z)\), \(h(x)\) y \(j(x,y,z)\).

clear 
clc
close all 

x=[-2*pi:0.01:2*pi];
y=[-2*pi:0.01:2*pi];
z=[-2*pi:0.01:2*pi];

f=(x-2).^2-3;
g=x.^2-3.*x.*y+2*x.^2;
h=sin(2*x).*cos(3*x)+4;
j=sin(x)+cos(x)+sin(2*x).*cos(y);

figure
subplot(2,2,1)
plot(x,f)
title("y=f(x)")
xlabel("x")
ylabel("y")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold');


subplot(2,2,2)
plot3(-cos(z),sin(z),z)
title("g(t)")
xlabel("x")
ylabel("y")
zlabel("z")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold');

subplot(2,2,3)
plot3(x,y,j)
title("j(x,y,z)")
xlabel("x")
ylabel("y")
zlabel("z")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold');

subplot(2,2,4)
plot(x,h)
title("h(x)")
xlabel("x")
ylabel("y")
grid
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold');

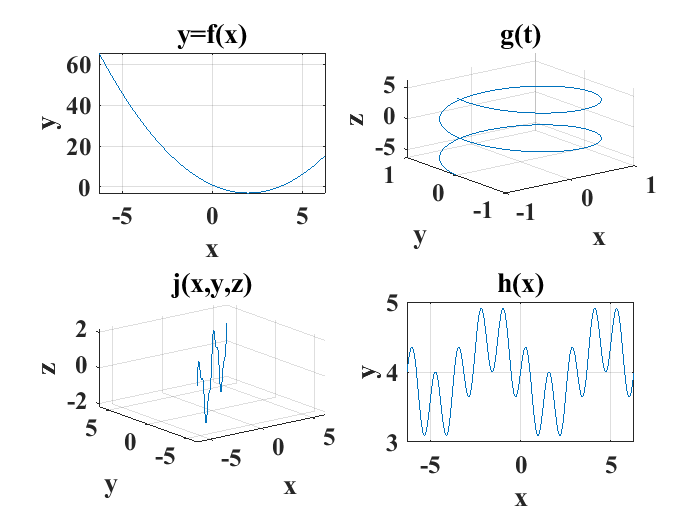
Finalmente, es posible guardar una figura de MATLAB® que contiene gráficas en diferentes extensiones de archivo: .fig para ser manejado directamente en MATLAB®, .png y .jpg para ser manejado como un archivo gráfico de propósito general como se muestra en el video de abajo:

Ejercicio de la práctica 9

1. Genere una figura en la que se incluyan las gráficas de las funciones \(y=cos(2x)\), \(w=sen(5x)\) y \(z=e^{-3.5x}\) usando los mismos ejes \(x\) e \(y\), donde \(0<x<2\pi\), con incrementos de \(0.05\pi\). Agrege título de la gráfica, rótulos a cada eje y cuadrícula, además incluya la leyenda que indique con claridad que curva corresponde a cada función.

2. El moviento de un proyectil se define por medio de las ecuaciones de movimiento en el plano:

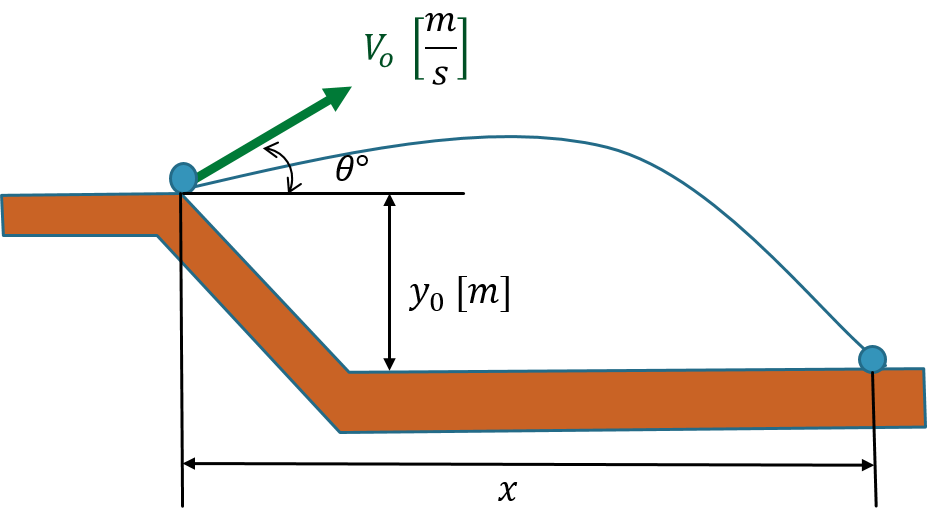
Figura 9 Tiro y trayectoria de un proyectil

\[\begin{split} \begin{eqnarray} x(t)=x_0+V_0cos(\theta)t\\ y(t)=y_0+V_0sen(\theta)t-\frac{9.81}{2}t^2 \end{eqnarray} \end{split}\]

Genere una figura en donde se muestre la gráfica de la trayectoria de un proyectil con \(y_0=15~[m]\) y \(x_0=10~[m]\)en los siguientes casos

a.\(V_0=30~[m/s]\), \(\theta=30°\) y \(\theta=60°\)

b.\(V_0=100~[m/s]\), \(\theta=30°\) y \(\theta=60°\)

Note que en total se generarán 4 curvas diferentes en la misma gráfica, use rótulos, colores y marcadores para distinguir cada caso, seleccione los rangos de \(x\), \(y\) y el intervalo correcto de \(t\) para una clara visualización de las trayectorias.

3. Guarde la gráfica generada en el punto aterior en los tres formatos siguientes:

   a) Figura de MATLAB® (extensión .fig)

   b) Figura de gráficos portables (extensión .png)

   c) Figura formato .pdf)

4. Genere una figura con tres sub-gráficas con los datos del archivo disponible en:

   https://raw.githubusercontent.com/LuisGerardo2204/Archivos_de_datos/main/ADC.txt

Use la primera columna de los datos como el vector de tiempo y las tres columans restantes como los datos a graficar contra el tiempo, use los comandos necesarios para dar a cada gráfica un titulo «Canal 1», «Canal 2» y «Canal 3» segun corresponda, anexe cuadrícula a cada sub-gráfica y rotule los ejes con las etiquetas \(t [s]\) y \(V_1\), \(V_2\) y \(V_3\) según corresponda. Fije los ejes de cada su-gráfica en un rango de \(0.2\) a \(0.7\) segundos y de \(0.5\) a \(3.5\) Volts.

5.- Grafique la curva tridimencional parametrizada con las siguientes ecuaciones:

\[\begin{split} \begin{eqnarray} &x=(3 + cos(\sqrt{32}t))cos(t)\\ &y=sen(\sqrt{32}t)\\ &z=(3 + cos(\sqrt{32}t))sen(t) \end{eqnarray} \end{split}\]

con \(0<t<40\pi\), use incremento de 0.01 para su vector de tiempo y proporciones rótulos a los ejes, título a la gráfica, use línea punteada color rojo y añada cuadrícula.