Práctica 13: Imágenes y animaciones#
En esta práctica se revisaran algunas funciones de MATLAB® que permiten la manipulación de archivos que contienen imágenes, para su visualización y análisis como variables. Además de su despliegue en figuras nativas, es decir, como elementos gráficos, es posible almacenar los componentes básicos en espacios de memoria en un formato de arreglos o matrices, lo cual permite la descomposición de las imágenes en los componentes de colores básicos rojo, azul y verde, además de su manipulación usando muchas de las importantes herramientas del álgebra lineal. En esta práctica se tratará con los imágenes representadas usando los colores primario Rojo, Verde y Azul, que son la base del estandard o formato RGB para la representación de imágenes en dispositivos electrónicos como lo son las computadoras y las pantallas de los sistemas inteligentes.
La unidad básica para la representación de las imágenes es el pixel, un pixel es entendido como una célula de una imágen. Una imágen se compone de miles o millones de estas unidades fundamnetales que a su vez se conforman de los tres colores primarios rojo, verde y azul, dado que la combinación de estos tres colores permite generar una amplia gama de colores y así representar imágenes. A cada pixel se le asignan tres variables que representan la intensidad de rojo, verde y azul en la imagen en ese punto en específico, en un rango de 0 a 255.
El comando básico para leer una imagen y almacenar su información pixel por pixel es imread() las impagenes se pueden leer desde archivos que se encuentren en la carpeta de trabajo, indicando la ruta al archivo si se encuentra en el disco duro en algún directorio diferente e inlcluso desde internet indicado la dirección completa.
clear
close all
clc
[A]= imread("https://raw.githubusercontent.com/LuisGerardo2204/Archivos_de_datos/refs/heads/main/juguete.png"); % Lectura y almacenamiento de una imagen en el arreglo A
whos A % Se muestran las características del arreglo A
Name Size Bytes Class Attributes
A 659x621x3 1227717 uint8
Como puede observarse, el arreglo A contiene 3 matrices de dimensiones 659x621. La primera matriz, es decir el elemento A(:,:,1) contiene la intensidad del color rojo de cada pixel, la matriz A(:,:,2) la intensidad del tono verde en cada pixel y finalmente la matriz A(:,:,3) la intensidad del color azul por pixel.
Para mostrar la imagen descargada o almacenada en el arreglo A se usa el comando imshow()
figure %Se inicializa una nueva figura
imshow(A) %Se despliega la imagen en la figura antes inicializada

Es posible visualizar la imagen en una figura con el formato de las gráficas con escala numérica, con la particularidad de que en los ejes se muestran las dimensiones en pixeles de la imagen:
figure
image([0 0],[0 0],A)%Se establece el origen como el punto incial para desplegar la imagen
% En los arreglos [x1 x2],[y1 y2]

La imagen se visualiza al combinar los tres colores primarios en cada pixel con las intesidades indicadas en cada uno de los elementos de la matriz A. Por ejemplo los componentes rojo, azul y verde en el pixel \(200,200\) de laimagen con la que se está trabajando son:
pixel_200_200=[A(200,200,1) A(200,200,2) A(200,200,3)]
pixel_200_200 = 1×3 uint8 32 79 38
El valor máximo de la intensidad para cada color rojo verde o azul es de 255. Las siguientes líneas de código ilustran la extracción de los colores en tres pixeles específicos:
close all
figure
subplot(1,2,1)
hold on
scatter(100,100,75,"MarkerFaceColor",[A(100,100,1) A(100,100,2) A(100,100,3)])
txt = "Pixel(100,100)";
text(120,100,txt,'FontSize',14)
scatter(300,300,75,"MarkerFaceColor",[A(300,300,1) A(300,300,2) A(300,300,3)])
txt = "Pixel(300,300)";
text(320,300,txt,'FontSize',14)
txt = "Pixel(500,180)";
text(200,500,txt,'FontSize',14)
scatter(180,500,75,"MarkerFaceColor",[A(500,180,1) A(500,180,2) A(500,180,3)])
axis([0 650,0,650])
set(gca,'Ydir','reverse')
subplot(1,2,2)
image([0 0],[0 0],A)%Se establece el origen como el punto incial para desplegar la imagen
% En los arreglos [x1 x2],[y1 y2]
hold on
scatter(100,100,75,"MarkerFaceColor",[A(100,100,1) A(100,100,2) A(100,100,3)])
txt = "Pixel(100,100)";
text(120,100,txt,'FontSize',14)
scatter(300,300,75,"MarkerFaceColor",[A(300,300,1) A(300,300,2) A(300,300,3)])
txt = "Pixel(300,300)";
text(300,300,txt,'FontSize',14)
scatter(180,500,75,"MarkerFaceColor",[A(500,180,1) A(500,180,2) A(500,180,3)])
txt = "Pixel(500,180)";
text(200,500,txt,'FontSize',14)
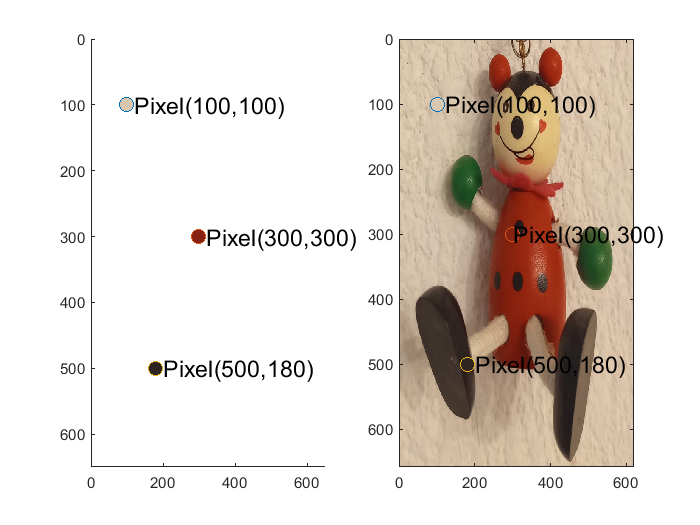
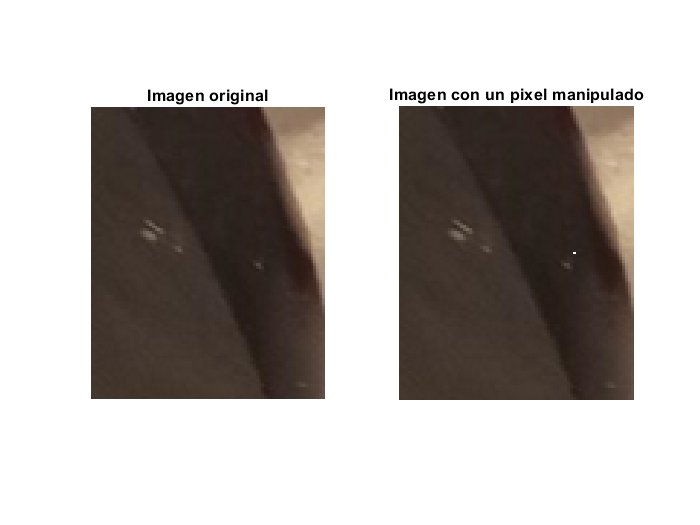
Con base en lo anterior, es posible asignar una tonalidad específica a un pixel o grupo de pixeles, por ejemplo, para manipular el pixel 500,180 y asignarle un color blanco es necesario asignarle el valor de 255 a cada uno de los componentes R,G y B de esa localidad en específico.
figure
subplot(1,2,1)
imshow(cat(3,A(450:550,120:200,1),A(450:550,120:200,2),A(450:550,120:200,3)))% Ajuste para despliegue de la imagen
title("Imagen original")
A(500,180,1)=255;
A(500,180,2)=255;%Manipulación del pixel (500,180)
A(500,180,3)=255;
subplot(1,2,2)
imshow(cat(3,A(450:550,120:200,1),A(450:550,120:200,2),A(450:550,120:200,3)))% Ajuste para despliegue de la imagen
title("Imagen con un pixel manipulado")
Operaciones de edición de forma de imágenes#
Las imágenes se pueden rotar, reflejar y presentar de forma invertida usando los comandos ´imrotate(I,grados)´, ´flipdim(I,2)´ y ´flipdim(I,1)´. Adicionalmente, las imágenes se pueden ampliar y reducir usando el comando ´imresize(I,factor)´. Por ejemplo, el resultado de aplicar operaciones tipo espejo y reflejo se ilustran con el siguiente código:
imagen_espejo=flipdim(A,2);%Se calcula el reflejo de la imagen y se almacena en un arreglo
imagen_reversa=flipdim(A,1);%Se calcula la reversa de la imagen y se almacena en un arreglo
imagen_espejo_reversa=flipdim(imagen_reversa,2);%Se hace un reflejo de la imagen invertida
figure
subplot(2,2,1)
imshow(A)
title("Imagen original")
subplot(2,2,2)
imshow(imagen_espejo)
title("Imagen espejo")
subplot(2,2,3)
imshow(imagen_reversa)
title("Imagen reversa")
subplot(2,2,4)
imshow(imagen_espejo_reversa)
title("Imagen espejo reversa")

Las componentes rojo, verde y azul se encuentran en las matrices individuales del arreglo.
Rojo = A(:,:,1);
Verde = A(:,:,2); %Descomposición de la intensidad de rojo, verde y azul de la imágen original
Azul = A(:,:,3);
figure
imshow(cat(3, Rojo, Verde, Azul))% Se despliega la imagen original usando sus componentes por separado

Para intensificar el azul en la figura original se puede sumar una constante a la matriz con los datos de la intensidad de ese tono primario:
figure
imshow(cat(3, Rojo, Verde, Azul+50))% Se despliega la imagen original usando sus componentes por separado
%con el color azul intensificado

La rotación de la imagen original con un ángulo de 60 grados se usa el comando imrotate() con la especificación bilineal:
imagen_rotada=imrotate(A,60,"Bilinear");
figure
imshow(imagen_rotada)

Las operaciones de amplificación y reducción se muestran en las siguientes líneas
imagen_amplificada=imresize(A,20,"nearest");
imagen_reducida=imresize(A,0.25,"nearest");
figure
imshow(A)
title("Imagen original")
figure
imshow(imagen_amplificada)
title("Imagen amplificada")
figure
imshow(imagen_reducida)
title("Imagen reducida")



disp("Dimensiones de la imagen original:")
whos A
disp("Dimensiones de la imagen ampliada:")
whos imagen_amplificada
disp("Dimensiones de la reducida:")
whos imagen_reducida
Dimensiones de la imagen original:
Name Size Bytes Class Attributes
A 659x621x3 1227717 uint8
Dimensiones de la imagen ampliada:
Name Size Bytes Class Attributes
imagen_amplificada 13180x12420x3 491086800 uint8
Dimensiones de la reducida:
Name Size Bytes Class Attributes
imagen_reducida 165x156x3 77220 uint8
Es posible modificar el contraste de las imájenes usando el comando imadjust(I,[minR minG minB;maxR maxG maxB],[])
imagen_ajustada_RGB=imadjust(A, [0.2 0.2 0.2; 0.4 0.4 0.4],[]);
imshow(imagen_ajustada_RGB)

Descomposicion de las imágenes en componentes HSV#
Una forma diferente de descomponer las imágenes es el formato HSV (Hue,Saturation,Value) que corresponden en español a los términos de matiz, saturación y brillo. El comando para la conversión de una imágen codificada en RGB a una codificada en formato HSV es rgb2hsv(I). Para mas información se puede consultar:
La representación en formato HSV de la imagen de ejemplo se muestra con las siguientes líneas de código:
HSI=rgb2hsv(A);
figure
subplot(2,2,1)
imshow(A)
title("Imagen original")
subplot(2,2,2)
imshow(HSI(:,:,1))
title("Matiz")
subplot(2,2,3)
imshow(HSI(:,:,2))
title("Saturación")
subplot(2,2,4)
imshow(HSI(:,:,3))
title("Intensidad")

Para cambiar el nivel de saturación de la imagen de ejemplo se manipula la matriz S del arreglo HSV creado:
figure
[H,S,V] = imsplit(HSI);%Se divide la matriz convertida
factor = 0.5;
S_saturada = S*factor; % Se afecta a la matriz de saturación
HSV_saturada = cat(3,H,S_saturada,V);
RGB_saturada = hsv2rgb(HSV_saturada);
imshow(RGB_saturada)
figure
[H,S,V] = imsplit(HSI);%Se divide la matriz convertida
factor = 1.8;
H_saturada = H*factor; % Se afecta a la matriz de saturación
HSV_saturada = cat(3,H_saturada,S,V);
RGB_saturada = hsv2rgb(HSV_saturada);
imshow(RGB_saturada)


Conversión a escala de grises#
Una imagen a color se puede convertir a su equivalente en escala de grises usando el comando rgb2gray() y tambien aplicando algunas operaciones a las matrices de valores rojo, verde y azul como se muestra en las siguientes líneas:
RGB_grises=rgb2gray(A); %Conversión de la imágen original a escala de grises
RGB_grises2=0.299*Rojo+0.587*Verde+0.114*Azul;
RGB_grises3=0.21*Rojo+0.72*Verde+0.07*Azul; %Tres técnicas diferentes de conversión a grises
RGB_grises4=(max(A,[],3)+min(A,[],3))/2;
figure
subplot(2,2,1)
imshow(RGB_grises)
title("Imagen original")
subplot(2,2,2)
imshow(RGB_grises2)
title("Conversión simple")
subplot(2,2,3)
imshow(RGB_grises3)
title("Estandard NTSC")
subplot(2,2,4)
imshow(RGB_grises4)
title("Luminosidad máxima")

Una alternativa más es representar a las imágnes en el formato de intensidades de color en gráficas tridimencionales:
[r,c,j]=size(A);% Se actualiza el tamaño de la imagen
figure
subplot(3,1,1)
surf(1:c,1:r,Rojo,'EdgeColor','none');
title("Rojo")
view(3)
subplot(3,1,2) % Se grafican en formato de intensidad los colores
surf(1:c,1:r,Verde,'EdgeColor','none');
zlabel('Intensidad del color')
view(3)
title("Verde")
subplot(3,1,3)
surf(1:c,1:r,Azul,'EdgeColor','none');
title("Azul")
view(3)
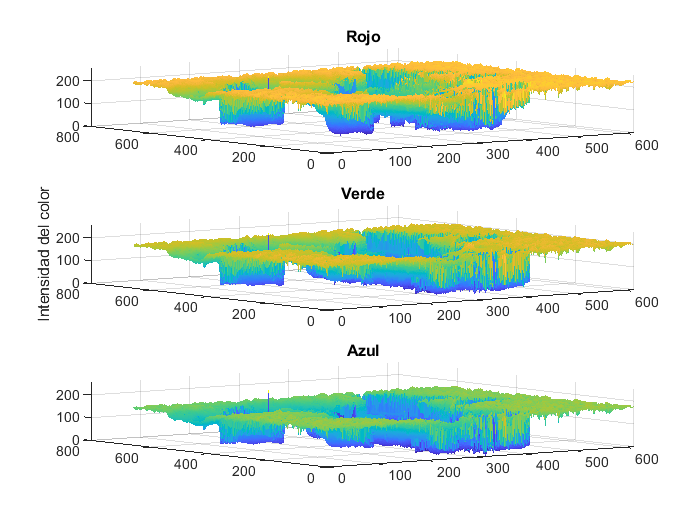
Animación de funciones#
Es posible realizar la animación de funciones en las gráficas generadas con MATLAB®, con el fin de integrar dinámica visual a los resultados numéricos que representan las gráficas de las funciones. Una de las formas de generar animaciones es generar una gráfica que se atualice cada cierto intervalo. Los siguientes ejemplos muestran la forma de generar animaciones de dos casos clásicos en física, el movimiento rectilíneo y el oscilador armónico.
Movimiento rectilíneo#
El movimiento rectilíneo es aquel que se puede representar en el plano usando una sola coordenada. Esta coordenada se modela como una función del tiempo y describe el movimiento de una partícula en términos de su posición respecto de un marco de referencia fíjo y su velocidad y aceleración definidas como:
\(x(t)=\) posición en metros.
\(v(t)=\frac{dx(t)}{dt}=\)velocidad en \([m/s]\).
\(a(t)=\frac{dx^2(t)}{dt^2}=\) aceleración en \([m/s^2]\).
El siguiente ejemplo permite generar la animación de un movimiento rectilíneo que describe una trayectoria oscilatoria en el eje \(x\), descrito por la expresión:
clear
close all
clc
% Creación del vector de tiempo
t=0:0.001:6;
%Se programa la expresión a animar
xt=4.5*sin(2*t);
uno=figure;
grid
axis([-5 5,-5 5])
%Se generan botones de control de animación especificndo su texto posición y color de fondo
handle=uicontrol('style','pushbutton','units','normal','backgroundcolor','red','position', ...
[0.85 .94 .13 .05],'String','Alto','callback','global stopstop;stopstop=1;');
handle2=uicontrol('style','pushbutton','units','normal','backgroundcolor','yellow','position', ...
[0.85 .87 .13 .05],'String','Pausa','callback','global ppause;ppause=1;');
handle3=uicontrol('style','pushbutton','units','normal','backgroundcolor','green','position', ...
[0.85 .8 .13 .05],'String','Reanudar','callback','global ppause;ppause=0;');
% Se da formato al texto de los ejes de las gráficas
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','x(t) [m]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x(t) [m]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Arial','FontWeight','normal');
global stopstop ppause;
ppause=0;
i=1;
stopstop =0;
% La animación se repetirá para cada valor de la función x(t) en cada instante de tiempo
while( i<5000&&stopstop==0)
cla
title(strcat('t= ',num2str((i-1)*0.001),' [s]',' x(t)= ',num2str(xt(i)),' [m]'))
hold on
plot([-5:0.001:5],0*[-5:0.001:5],'k -','LineWidth',2)%Se grafica la paríticula
plot(t(1:i),xt(1:i),'b -','LineWidth',2) %Actualización de la posición de la partícula
rectangle('Position',[xt(i) 0.0 0.24 0.24],'FaceColor',[0 .5 .5],'Curvature',0.5)% Se dibuja la partícula
pause(0.001)
while ppause==1
pause(.001)%Acción del botón de pausa
end
i=i+10;
cla %pausa para animación
end
close(uno)
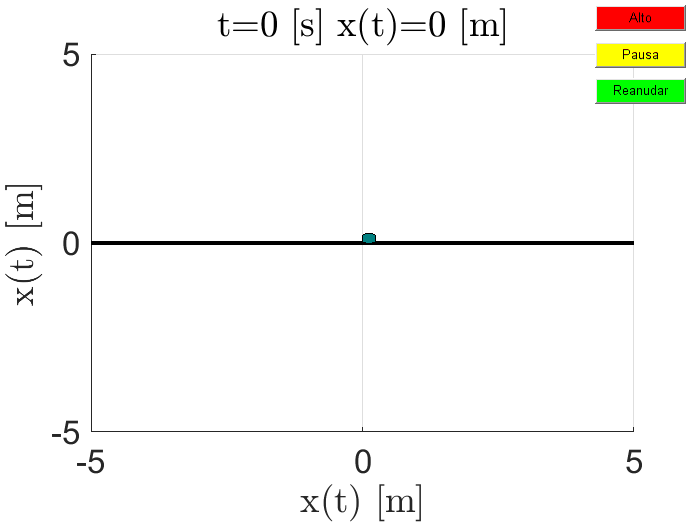
Sistema oscilador armónico.#
Un sistema masa-resorte-amortiguador se considera como un oscilador armónico y se modela matemáticamente usando la ecuación diferencial:
Donde \(y(t)\) es la solución de la ecuación diferencial (12) y representa al desplazamiento en metros de la masa \(m\) respecto del punto de equilibrio, \(m\) es la masa en \([kg]\), \(b\) la constante de amortiguador con unidades \([Ns/m]\) y \(k\) en unidades \([N/m]\). además \(f(t)\) es la fuerza externa. En una práctica posterior se retomará este modelo para hacer simulaciones en el entorno gráfico simulink®.
La solución general para el caso de vibraciones libres, es decir, cuando \(f(t)=0\) y por lo menos alguna de las condiciones iniciales de posición \(y(0)\) en \([m]\) o velocidad \(v(0)\) en \([m/s]\) es
donde \(\omega_d\) y \(\beta\) son la frecuencia natural mortiguada y \(\beta\) una constante dadas por:
clear
close all
clc
%Se lee la imagen del juguete a animar como oscilador armónico
A=imread("https://raw.githubusercontent.com/LuisGerardo2204/Archivos_de_datos/refs/heads/main/juguete.png");
% Parámetros del sistema masa-resorte-amortiguador
m=0.43;
b=0.15;
k=4.5;
%condiciones iniciales de posición y velocidad
y0=0.025;
dy0=0.0;
% Cálculo de la frecuencia natural amortiguada
wd=sqrt(k/m-b^2/(4*m^2));
% Constante de la solución omogénea
a=(m*dy0+b*y0)/(m*wd);
%vector de tiempo
t=0:0.001:15;
% Función x(t)
yt=exp((-b/(2*m)).*t).*(y0*cos(wd.*t)+a*sin(wd.*t));
dos=figure;
i=1;
% La animación se repetirá para cada valor de la función x(t) en cada instante de tiempo
while((i<max(t)*1000))
cla
subplot(1,2,1)
hold on
plot([-max(t):0.001:max(t)],0*[-max(t):0.001:max(t)],'k -','LineWidth',2)
plot(t(1:i),yt(1:i),'b -','LineWidth',2)
axis([0 max(t),-0.035 0.035])
% Se da formato al texto de los ejes de las gráficas
set(get(gca,'XLabel'),'String','t [s]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',12)
%
set(get(gca,'YLabel'),'String','y(t) [m]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',12)
set(gca,'fontsize',12);
set(gca,'fontname','Arial','FontWeight','normal');
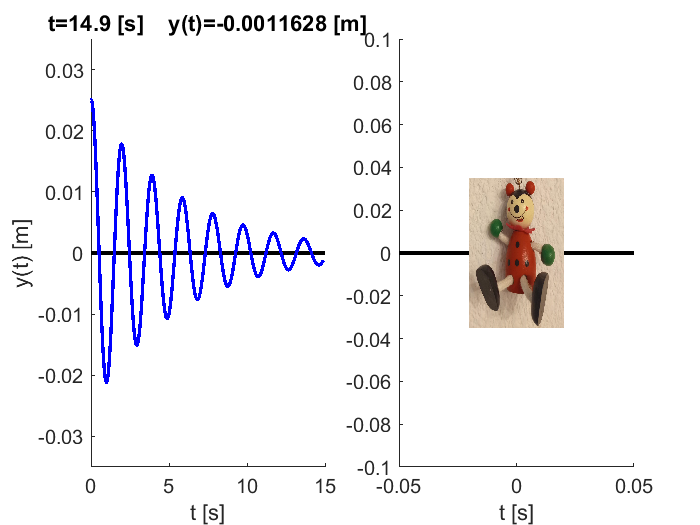
title(strcat('t= ',num2str((i-1)*0.001),' [s]',' y(t)= ',num2str(yt(i)),' [m]'))
% Se da formato al texto de los ejes de las gráficas
subplot(1,2,2)
hold on
plot([-max(t):0.001:max(t)],0*[-max(t):0.001:max(t)],'k -','LineWidth',2)
image([-0.02 0.02],[yt(i)+0.035 yt(i)-0.035],A); %Se inserta la imagen a animar en la gráfica
axis([-0.05 0.05,-0.1 0.1]) % Ajuste de coordenadas para visualización
%Se da formato y tamaño de letra a la gráfica animada
set(get(gca,'XLabel'),'String','t [s]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',12)
set(gca,'fontsize',12);
set(gca,'fontname','Arial','FontWeight','normal');
i=i+100;
pause(0.01)% pausa para animación
cla
end
% Se grafica la imágen en el punto de equilibrio original al terminar la animación
subplot(1,2,2)
hold on
plot([-max(t):0.001:max(t)],0*[-max(t):0.001:max(t)],'k -','LineWidth',2)
image([-0.02 0.02],[0.035 -0.035],A);
axis([-0.05 0.05,-0.1 0.1])
set(get(gca,'XLabel'),'String','t [s]',...
'FontName','Arial',...
'FontAngle','normal',...
'FontSize',12)
set(gca,'fontsize',12);
set(gca,'fontname','Arial','FontWeight','normal');
Ejercicio de la práctica 13#
1.- Descargue o lea desde la ruta las siguientes imágenes:
https://raw.githubusercontent.com/LuisGerardo2204/Archivos_de_datos/refs/heads/main/flores.JPG https://raw.githubusercontent.com/LuisGerardo2204/Archivos_de_datos/refs/heads/main/cedral.jpg
Realice las siguientes operaciones con las dos imágenes:
a) En una figura muestre la imagen original, la imagen en escala de grises, la imagen invertida y la imagen escalada al 25% de su tamaño original.
b) En otra figura muestre la imagen original y su versión en el formato HSV con el factor 0.8 aplicado a la matriz de color o matiz.
c) En una tercer figura muestre la imagen original y la figura con las siguientes transformaciones:
donde \(R\) es la matriz componente rojo, \(B\) es la matriz componente azul y \(G\) es la matriz componente verde. Use el comando imshow(cat(3,Y,I,Q)) para mostrar la imagen transformada.
2.- Realice la animación de la gráfica \(y(t)\) para un sistema masa-resorte con condiciones iniciales \(y(0)=0.015~[m]\), velocidad inicial \(v(0)=0~[m/s]\), masa \(m=0.5~[kg]\) y constante de rigidez \(k=300~[N/m]\). Considere que la ecuaciones (13) para construir la ecuación para simular el caso particular que se plantea.
3.- Realice la animación de la gráfica de uno de los casos del tiro parabólico del ejercicio 2 de la Práctica 9.
