Práctica 10: Otros tipos de gráficas

En ingeniería, las gráficas de dos variables son muy comunes dada su capacidad de transmitir de forma muy visual e instantánea la evolución de una magnitud en el tiempo o con respecto a otra varable de interés. Existen gráficas de otras naturalezas que también permiten la representación y análisis visual de datos, existen aplicaciones en las cuales tipos de gráfica muy diferentes en estructura a las de dos variables son much más explicitas y permiten obtener conclusiones de análisis con mejores bases o argumentos.

Gráficas bidimencionales alternativas

La gráfica polar

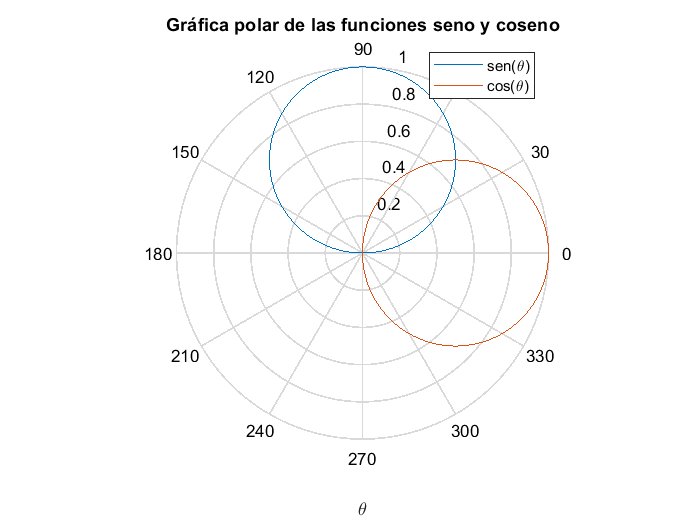
Una gráfica polar es una representación del tipo línea que se traza de forma circular de forma que la variable independiente, (eje \(x\)) es un ángulo y la variable dependiente (eje \(y\)) es una magnitud. En MATLAB®, el comando para generar una gráfica polar es polar(r,\(\theta\))

clear
close all
theta=[-pi:0.001:pi];
r1=sin(theta);
r2=cos(theta);
polar(theta,r1)
hold on 
polar(theta,r2)
title("Gráfica polar de las funciones seno y coseno")
legend("sen(\theta)","cos(\theta)")
xlabel("\theta")

Gráficas con escala logarítmica

En ingeniería hay ocasiones en las que una escala con incrementos monótonos como los que hemos utilizado hasta el momento no son adecuadas por que una de las variables, ya sea la variable independiente o la dependiente tienen cambios en escalas con intervalos muy grandes. Por ejemplo, si se considera la gráfica de un polinomio como \(y=5x^4-2x^2-45x+10\), es dificil visualizar la curva con detalle cuando se consideran rangos amplios para la variable \(x\), por ejemplo para el intervalo \(-10<x<10\) la gráfica adquiere la siguiente forma:

close all
x=[0:0.01:70];
y=5*x.^4;
plot(x,y)
xlabel("x")
ylabel("y")
grid

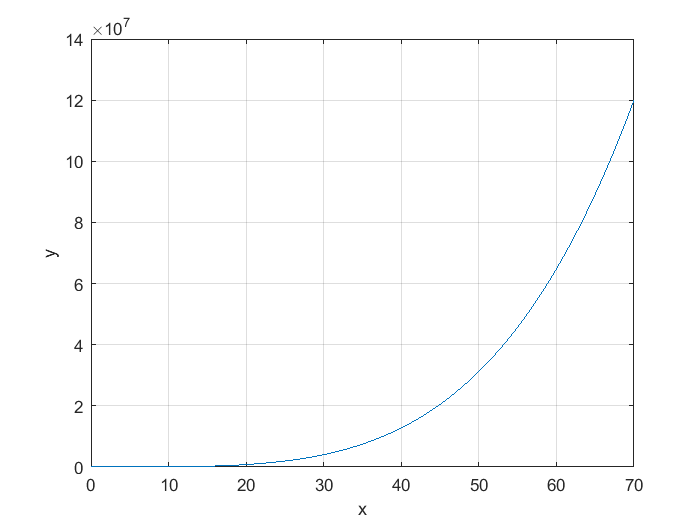
Una alternativa a la necesidad de usar valores tan grandes, en ingenería se recurre a la escala logaritmimca. En una escala lograírmica se usa la base 10, este tipo de escala tiene la ventaja de que no comprime los valores pequeños como sucede en el ejemplo anterior, note que en la gráfica del polinomio no se puede distinguir con claridad a loa valores entre \(10\) y \(-10\). LA gráfica en escala logarítmica del ejemplo anterior se realiza al utilizar el comando semilogx() como se muestra a continuación:

close all
semilogx(x,y)
grid
xlabel("x")
ylabel("y")

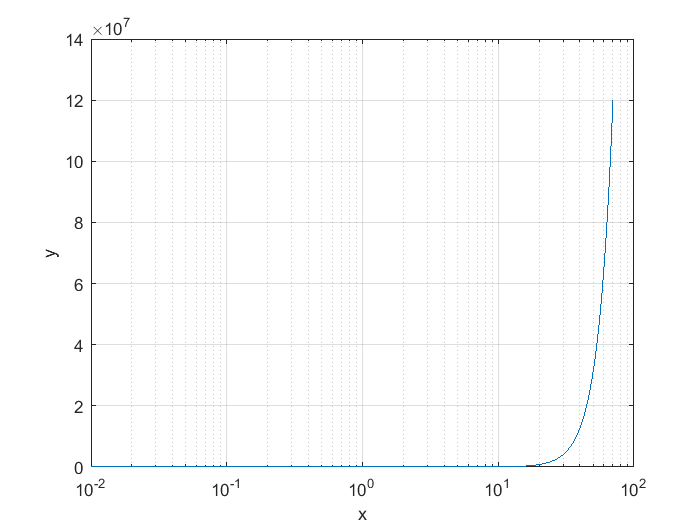
En esta última gráfica, se puede apreciar un rango de valores más aplio en el eje \(x\), la escala abarca el doble, dado que en la gráfica original el máximo valor en el eje \(x\) es 50. Dada la naturaleza de la función que se está graficando, el valor de \(y\) aumenta muy rápidamente con respecto a la variable \(x\), dado que su razón de cambio o derivada es un polinomio de tercer grado. La magnitud de \(y\) se puede compactar usando la escala logaritmica, tambien por medio del comado de graficación semilogy(), note que el comando indica el eje que se desea representar en escala logarítmica en la gráfica que se está generando:

close all
semilogy(x,y)
grid
xlabel("x")
ylabel("y")

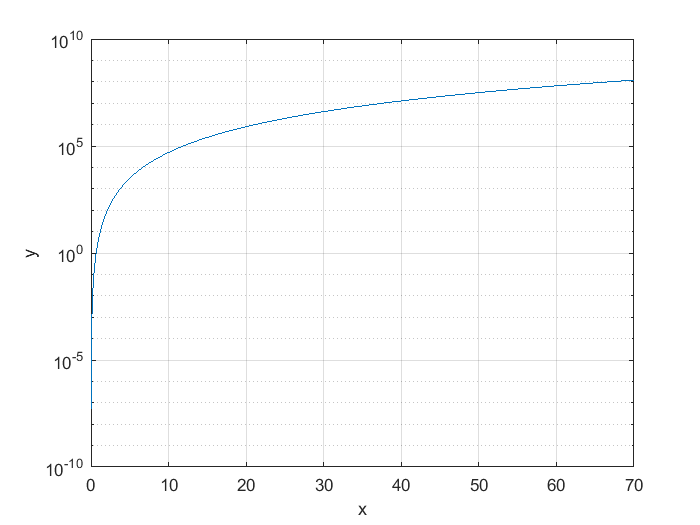
Si bien se redujo visualmente la velocidad de crecimiento de la variable \(y\), sigue mostrando una tendencia de crecimiento que no permite visualizar de forma condensada mas valores de \(y\) cuando \(x\) se incrementa más allá de 50. Una tercera solución es usar escala logarítmica en ambos ejes, usando el comando de graficación loglog().

close all
loglog(x,y)
grid
xlabel("x")
ylabel("y")

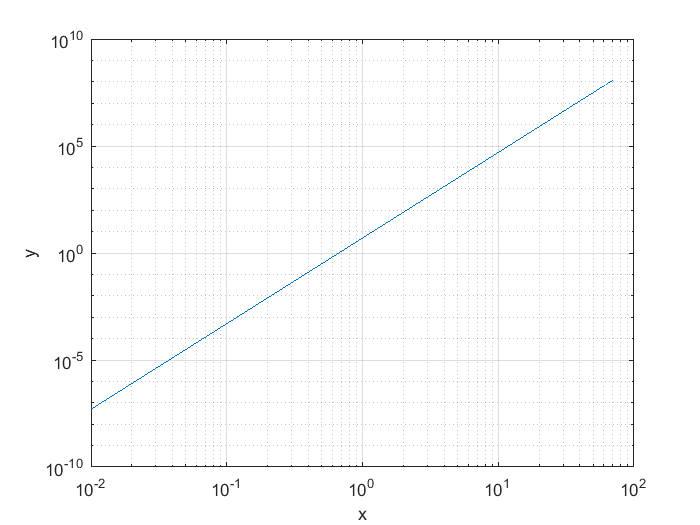
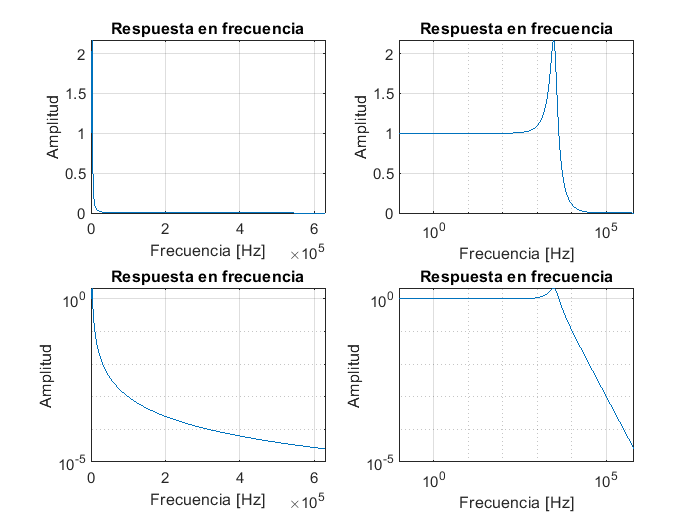
Las gráficas con escala logaritmica son especialemente útiles en ingeniería electrónica para representar el comportamiento o respuesta en frecuencia de los amplificadores dada el amplio rango de frecuencias que se manejan. Por ejemplo, la respuesta en frecuencia de un circuito RLC serie (resistecia, inductrancia capacitancia) se presenta en variable compleja como se muestra en el siguiente código:

clear 
close all
clc
frecuencia=[0.1:0.1:2*pi*100000]; %Rango de frecuencias de $0.1$ a $100$ $KHz$
%Parámetros del sistema 
L=100e-3;
C=1e-6;
R=150;
%Cálculo de la respuesta en frecuencia del sistema ante una entrada sinusoide
% Se mide el voltaje en el capacitor como salida.
Vw=1./(L*C*(i*frecuencia).^2+R*C*(i*frecuencia)+1);

subplot(2,2,1)
plot(frecuencia,abs(Vw))
title("Respuesta en frecuencia")
xlabel("Frecuencia [Hz]")
ylabel("Amplitud")
grid

subplot(2,2,2)
semilogx(frecuencia,abs(Vw))
title("Respuesta en frecuencia")
xlabel("Frecuencia [Hz]")
ylabel("Amplitud")
grid


subplot(2,2,3)
semilogy(frecuencia,abs(Vw))
title("Respuesta en frecuencia")
xlabel("Frecuencia [Hz]")
ylabel("Amplitud")
grid

subplot(2,2,4)
loglog(frecuencia,abs(Vw))
title("Respuesta en frecuencia")
xlabel("Frecuencia [Hz]")
ylabel("Amplitud")
grid

Gráficas de barra y circulares para estadística.

Las gráficas de barras y circulares permiten una presentación visual de conjuntos de datos que resulta muy atractivas dada su facilidad de lectura e interpretación. En MATLAB®, los comandos para generar gráficas estadísticas son los mostrados en la Tabla 13.

Tabla 13 Tabla de instrucciones de graficación.

Comando MATLAB\(^{\textregistered}\)	Descripción
bar(x)	Genera una gráfica de barras vertical de los datos almacenados en el vector x
barh(x)	Genera una gráfica de barras horizontal de los datos almacenados en el vector x
bar3(x)	Genera una gráfica de barras tridimencional de los datos almacenados en el vector x
bar3h(x)	Genera una gráfica de barras tridimencional y horizpntal de los datos almacenados en el vector x
pie(A)	Genera una gráfica circular de los datos almacenados en la matriz A
pie3(A)	Genera una gráfica circular tridimencional de los datos almacenados en la matriz A

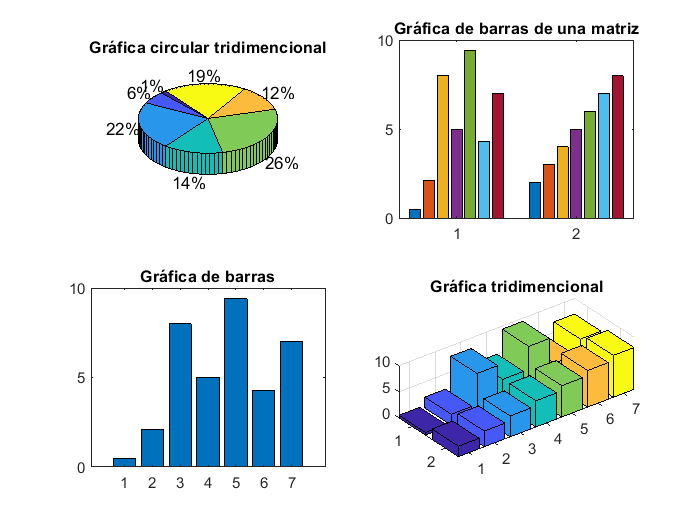
Para ejemplificar los tipos de gráficos mencionados en la tabla, los siguientes comandos sirven para graficar en una misma figura, todos los tipos de gráfica con un conjunto de datos de ejemplo:

clear
clc
close all

a=[0.5,2.1,8,5,9.4,4.3,7];
b=[a;2:8];

subplot(2,2,1)
pie3(a)
title("Gráfica circular tridimencional")

subplot(2,2,2)
bar(b)
title("Gráfica de barras de una matriz")
subplot(2,2,3)
bar(a)
title("Gráfica de barras")

subplot(2,2,4)
bar3(b)
title("Gráfica tridimencional")

Gráficas con dos ejes de escalas diferentes.

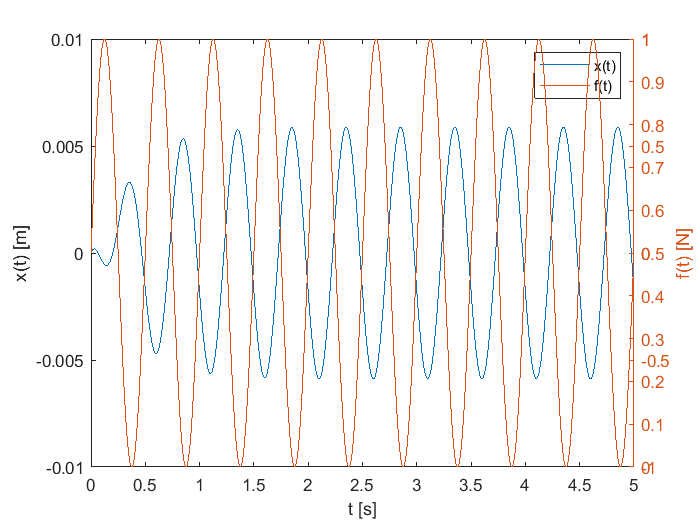
En ingeniería resulta de utilidad, en ocasiones, el sobreponer dos gráficas de dos dimensiones en una misma figura. Pero en no pocas ocasiones sucede que no son compatibles las magnitudes de las curvas que se desean contrastar o graficar en la misma figura. Por ejemplo, considérese el caso de un sistema masa-resorte-amortiguador cuya salida es un desplazamiento \(x(t)\) en unidades de metros. Se desea contrastar con la fuerza de entrada que actúa sobre la masa con orden de Newtons. suponiendo que las funciones para la fuerza y el desplazamiento son:

\[\begin{split} \begin{eqnarray} &f(t)=sen(4\pi t)~[N]\\ &x(t)=e^{-3t}(0.0018cos(\sqrt{149}t)+0.0073sen(\sqrt{149}t))-0.0018cos(4\pi t)-0.0056sen(4\pi t)~[m] \end{eqnarray} \end{split}\]

Para contrastar la salida del sistema con la fuerza de entrada se grafica en una misma gráfica o par de ejes cordenados las dos funciones \(x(t)\) y \(f(t)\).

clear
close all
clc

t=[0:0.001:5];

f=sin(4*pi*t);
x=exp(-3*t).*(0.0018*cos(sqrt(149)*t)+0.0073*sin(sqrt(149)*t))-0.0018*cos(4*pi*t)-0.0056*sin(4*pi*t);

plot(t,x)
hold on 
plot(t,f)
xlabel("t [s]")

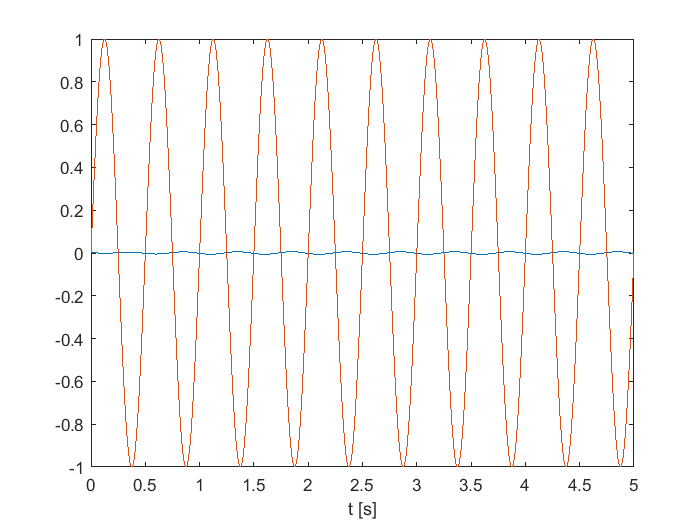
Como se observa en la gráfica anterior, es imposible comparar las dos magnitudes dada la gran diferencia en sus magnitudes. En MATLAB®, es posible juntar ambas gráficas usando el comando plotyy() para generar una gráfica de datos que adapte las escalas para poder contrastar dos curvas, como se muestra en el siguiente código:

figure 

plotyy(t,x,t,f)
legend("x(t)","f(t)")
ylabel("x(t) [m]")
xlabel("t [s]")
yyaxis right
ylabel("f(t) [N]")

Ejercicio de la práctica 10

1. Defina un vector o arreglo llamado \(angulo\) en el intervalo \([0,2\pi]\), con un incremento de \(0.01\pi\). Defina un arreglo de distancias \(d=7cos(4.5*angulo)\). Elabore una gráfica polar de \(angulo\) contra \(d\).

2. Use el comando hold on para graficar en la figura del punto anterior \(d=3cos(6.5*angulo)\).

3. En una nueva figura, use el mismo arreglo \(angulo\) para graficar \(d=\sqrt(25cos(2angulo))\), en una gráfica polar.

4. Genere arreglos \(x\) e \(y\) para graficar cada una de las funciones que se expresan en el conjunto de ecuaciones (11) . Use el comando subplot para repartir las gráficas de manera que se presenten en una sola figura, con los siguientes tipos de gráfica

• \(y_1\) escala lineal.

• \(y_2\) semilogarítmica en el eje \(x\).

• \(y_3\) semilogarítmica en el eje \(y\).

• \(y_4\) escala logarítmica en ambos ejes.

(11)\[\begin{split}\begin{eqnarray} &y_1=7x+4\\ &y_2=4x^2\\ &y_3=14e^{(x+3)}\\ &y_4=\frac{1}{(2x)} \end{eqnarray}\end{split}\]

Indique cuales de los formatos producen una línea recta.

5. Genere dos gráficas de reporte de datos con la información de la tabla siguiente:

\(t\) \([s]\)	\(T_1\) \(°C\)	\(T_2\) \(°C\)	\(T_3\) \(°C\)	\(T_4\) \(°C\)	\(T_5\) \(°C\)
0.000	22.430	24.404	23.194	21.199	20.595
1.000	22.398	24.278	23.364	21.223	20.762
2.000	22.341	24.239	23.213	21.150	20.340
3.000	22.422	24.419	23.133	21.155	20.479
4.000	22.215	24.457	23.101	21.371	20.589
5.000	22.434	24.391	23.268	21.230	20.604
6.000	22.424	24.383	23.284	21.423	20.819
7.000	22.442	24.344	22.920	21.488	20.495
8.000	22.423	24.313	23.478	21.212	20.828
9.000	22.353	24.469	22.980	21.306	20.813
10.000	22.395	24.404	22.963	21.314	20.578

a) Genere una grafica de barras con los promedios de cada una de las cinco columnas de temperatura.

b) Genere una gráfica circular, tridimencional con los valores de temperatura de toda la tabla que se encuentren en los siguientes intervalos de temperatura:

b.1)\(20°<T<21.5°\)

b.2)\(22°<T<23°\)

b.3)\(23°<T<24°\)

b.4)\(24<T<24.5°\)

c) Genere una gráfica de barras tridimencional de los datos de temperatura de todas las columnas para los 5 primeros datos.

Coloque los rótulos para los ejes, título y tamaño de fuente adecuados en todas sus gráficas.