Práctica 15: Simulación de sistemas dinámicos parte 2

En la sección pasada se presentaron los conceptos básicos para generar simulaciones en el ambiente gráfico de simulación, es decir, se presentó la simulación de un par de sistemas dinámicos en el formato de diagrama de bloques usando la herramienta gráfica Simulink®. En esta práctica haremos simulaciones de sistemas dinámicos más complejos haciendo uso de bloques especiales que permiten la creación de funciones embebidas, las cuales son funciones creadas por el usuario conforme a sus propias necesidades de entradas y salidas.

Escritura de funciones embebidas

Como primer ejemplo, crearemos un diagrama de bloques que permite la multiplicación de una matriz por dos vectores diferentes que se pueden seleccionar con un bloque del tipo interruptor.

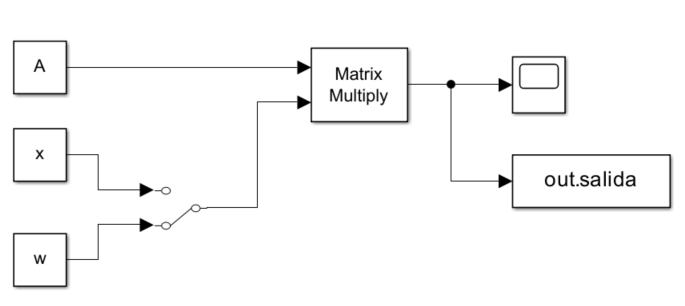
Figura 16 Diagrama de bloques para una multiplicación de dos arreglos.

Los bloques que contienen las matrices y vectores para la multiplicación se obtienen en la sección de bloques comúnmente usados, que están contenidos en la librería de bloques de , como se muestra en la Figura 15, de la práctica 14 y en la Figura 17 de esta práctica , de manera que son los que se identifican con el nombre de constantes:

Figura 17 Bloques de constantes.

Figura 18 Bloque selector.

La construcción del diagrama de blouqes que se muestra en la Figura 16 implica usar un bloque de direccionamiento de señal, denoninado Manual Switch el cual se obtiene en la sección signal routing, como se muestra en la Figura 18.

El uso de un bloque especial para la multiplicación de matrices, existen varios bloques que son específicos para realizar operaciones con matrices como se muestra en la Figura 19:

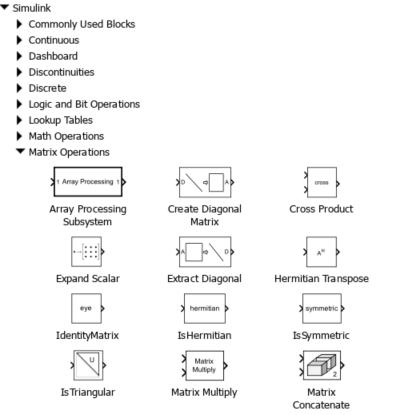
Figura 19 Bloques de operaciones con matrices.

Para poder simular el diagrama de bloques que se muestra en la Figura 16 es necesario construir las matrices A, x y w en el espacio de trabajo de MATLAB® usando el command window:

clear 
close all

A=[4 -3 2;
   2  6 -8;
   1 3.5 4]

x=[1;-3;7]

w=[-4;5;8]

A = 3×3 double
    4.0000   -3.0000    2.0000
    2.0000    6.0000   -8.0000
    1.0000    3.5000    4.0000

x = 3×1 double
     1
    -3
     7

w = 3×1 double
    -4
     5
     8

El resultado de la multiplicación de la matriz \(A\) por los dos vectores diferentes es: dos matrices es:

\[\begin{split} Ax=\begin{bmatrix}4&-3&2\\2&6&-8\\1&3.5&4\end{bmatrix}\begin{bmatrix}1\\-3\\7\end{bmatrix}=\begin{bmatrix}27\\-72\\18.5\end{bmatrix} \end{split}\]

\[\begin{split} Aw=\begin{bmatrix}4&-3&2\\2&6&-8\\1&3.5&4\end{bmatrix}\begin{bmatrix}-4\\5\\8\end{bmatrix}=\begin{bmatrix}-15\\-42\\45.5\end{bmatrix} \end{split}\]

Lo cual se puede comprobar usando la instrucción:

disp("Multiplicación Ax:")
A*x
disp("Multiplicación Aw:")
A*w

Multiplicación Ax:

ans = 3×1 double
   27.0000
  -72.0000
   18.5000

Multiplicación Aw:

ans = 3×1 double
  -15.0000
  -42.0000
   45.5000

Es posible ontener el resultado de las operaciones anteriores usando el diagrama de blouqes que se muestra en la Figura 16, el resultado de ejecutar dicho diegrama de bloques es se muestra en la Figura 20:

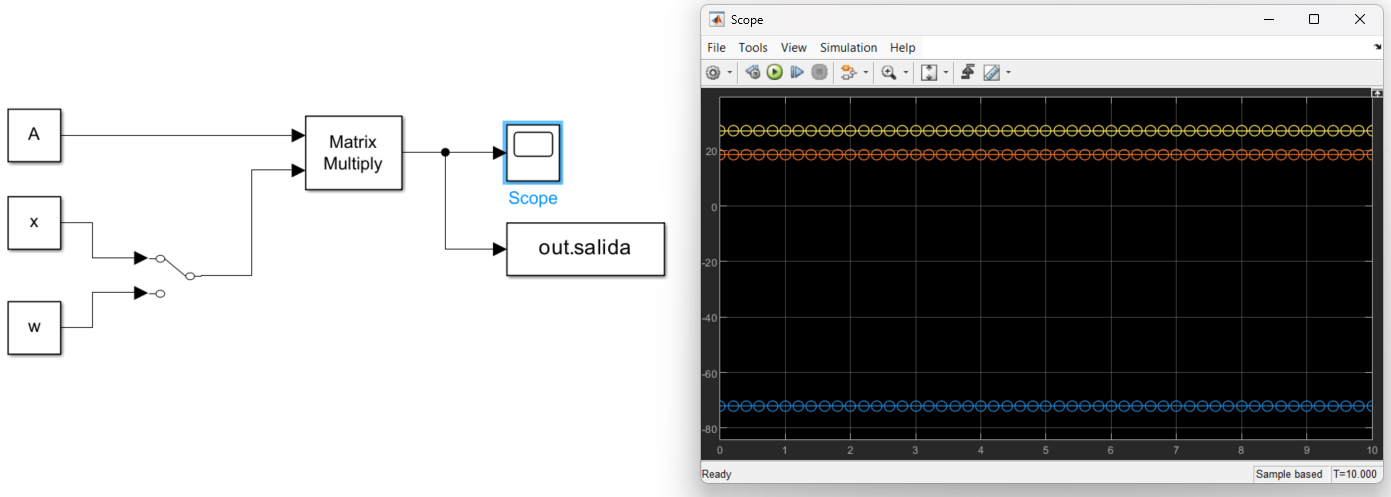
Figura 20 Resultado gráfico de la simulación del diagrama de bloques.

El resultado de esta operación se ha almacenado en la variable tipo objeto llamada out. Los detalles de esa variable contienen los resultados de la simulación del diagrama de bloques que se utilizó para la solución de la multiplicación de las matrices, como se muestra en la Figura 21.

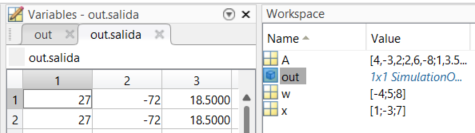
Figura 21 Variable de salida que contiene el resultado de la operación matricial.

Con base en los resultados de la simulación del diagrama de bloques anterior, podemos concluir que la simulación en el ambiente gráfico no se limita a variables escalares, es decir a números, sino que también podemos simular sistemas de múltiples entradas y múltiples salidas. En la teoría del modelado de sistemas dinámicos es común utilizar sistemas de ecuaciones, dado que los sistemas no siempre se constituyen de una sola entrada y una sola salida como los ejemplos que se trataron en la sección pasada, es decir los sistemas modelados por las ecuaciones (16) y (18).

Sistema mecánico vibratorio de dos grados de libertad

Los sisntemas dinámicos analizados en la práctica 14 se denominan de un solo grado de libertad por que basta una sola coordenada o variabla para describir su comportamiento completamente. Dicho de otra manera, la solución de la ecuación diferencial que modela al sistema basta para describir por completo al sistema. En esta práctica trataremos con sistemas de más de un grado de libertad, por ejemplo, dos masas acopladas por medio de un resorte o un circuito eléctrico de dos mallas.

Considere el sistema mostrado en la Figura 22. Si las fuerzas de excitación son iguales a cero, y las condiciones iniciales son no nulas o diferentes de cero, se dice que el sistema se encuentra en condiciones de vibraciones libres.

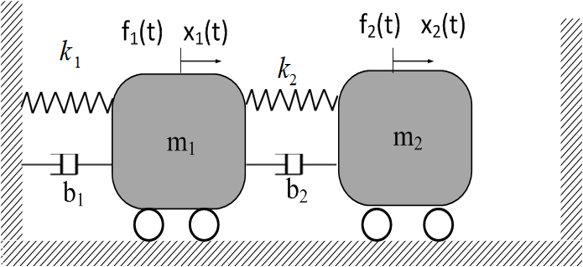
Figura 22 Sistema mecánico vibratorio de dos grados de libertad.

Donde \(m_i\), son las masas en \(Kg\), \(b_i\) son las constantes de amortiguamiento viscoso en \(Ns/m\) y \(k_i\) son las constantes de rigidez en \(N/m\), con con \(i=1,2\). Para esta configuración en particular, el modelo matemático no es una ecuación diferencial sino un sistema de dos ecuaciones diferenciales:

(19)\[\begin{split}\begin{eqnarray} m_1\ddot{x}_1+(b_1+b_2)\dot{x}_1-b_2\dot{x}_2+(k_1+k_2)x_1+k_2x_2=f_1\\ m_2\ddot{x}_2-b_2\dot{x}_1-b_2\dot{x}_2-k_2x_1+k_2x_2=f_2 \end{eqnarray}\end{split}\]

La cual se puede expresar en forma matricial como:

(20)\[\begin{equation} M\ddot{x}+B\dot{x}+Kx=f \end{equation}\]

donde \(x=\begin{bmatrix}x_1\\x_2\end{bmatrix}\in R^2\), \(f=\begin{bmatrix}f_1\\f_2\end{bmatrix}\in R^2\) y las matrices \(M\in R^{2\times 2}\), \(M\in R^{2\times 2}\) y \(M\in R^{2\times 2}\) son tales que:

\[\begin{split} M=\begin{bmatrix}m_1&0\\0&m_2\end{bmatrix},~~~~B=\begin{bmatrix}b_1+b_2&-b_2\\-b_2&b_2\end{bmatrix}~~~~K=\begin{bmatrix}k_1+k_2&-k_2\\-k_2&k_2\end{bmatrix} \end{split}\]

Estas matrices tienen propiedades especiales:

• Son matrices con cada una de sus entradas en los números reales

• Son matrices simétricas, se cumple que son iguales a sus versiones transpuestas, es decir \(M=M^T,~~B=B^T,~~K=K^T\), por ejemplo:

(21)\[\begin{split}M=\begin{bmatrix}\textcolor{green}{m_1}&\textcolor{green}{0}\\\textcolor{red}{0}&\textcolor{red}{m_2}\end{bmatrix}=M^T=\begin{bmatrix}\textcolor{green}{m_1}&\textcolor{red}{0}\\\textcolor{green}{0}&\textcolor{red}{m_2}\end{bmatrix}\end{split}\]

(22)\[\begin{split}B=\begin{bmatrix}\textcolor{green}{b_1+b_2}&\textcolor{green}{-b_2}\\\textcolor{red}{-b_2}&\textcolor{red}{b_2}\end{bmatrix}=B^T=\begin{bmatrix}\textcolor{green}{b_1+b_2}&\textcolor{red}{-b_2}\\\textcolor{green}{-b_2}&\textcolor{red}{b_2}\end{bmatrix}\end{split}\]

(23)\[\begin{split}K=\begin{bmatrix}\textcolor{green}{k_1+k_2}&\textcolor{green}{-k_2}\\\textcolor{red}{-k_2}&\textcolor{red}{k_2}\end{bmatrix}=K^T=\begin{bmatrix}\textcolor{green}{k_1+k_2}&\textcolor{red}{-k_2}\\\textcolor{green}{-k_2}&\textcolor{red}{k_2}\end{bmatrix}\end{split}\]

Por ejemplo, si al sistema mecánico descrito en la Figura 22 se le asignan los valores numéricos de la Tabla 17.

Tabla 17 Tabla de parámetros

\[Parámetro\]	\[Valor\]
\[m_1\]	\[2.45~[Kg]\]
\[m_2\]	\[2.75~[Kg]\]
\[b_1\]	\[5~[Ns/m]\]
\[b_2\]	\[3~[Ns/m]\]
\[k_1\]	\[350~[N/m]\]
\[k_2\]	\[300~[N/m]\]
\[f_1\]	\[4u(t)~[N]\]
\[f_2\]	\[2u(t)~[N]\]

Con condiciones iniciales nulas, es decir \(x_1(0)=x_2(0)=0~[m]\) y \(\dot{x}_1(0)=\dot{x}_2(0)=0~[m/s]\). El modelo o sistema de ecuaciones del sistema resultante se describe como:

\[\begin{split} \begin{bmatrix}2.25&0\\0&2.75\end{bmatrix}\begin{bmatrix}\ddot{x}_1\\\ddot{x}_2\end{bmatrix}+\begin{bmatrix}9&-5\\-5&5\end{bmatrix}\begin{bmatrix}\dot{x}_1\\\dot{x}_2\end{bmatrix}+\begin{bmatrix}650&-300\\-300&300\end{bmatrix}\begin{bmatrix}{x}_1\\{x}_2\end{bmatrix}=\begin{bmatrix}4u(t)\\2u(t)\end{bmatrix} \end{split}\]

Despejando el vector \(\ddot{x}=[\ddot{x}_1~~\ddot{x}_2]^T\) se puede expresar un diagrama de bloques de manera similar al que se usó en la práctica anterior, con la diferencia fundamental de que se trabaja con vectores y matrices en vez de valores escalares. La expresión resultante es:

\[\begin{split} \begin{bmatrix}\ddot{x}_1\\\ddot{x}_2\end{bmatrix}=\begin{bmatrix} \frac{1}{2.25}&0\\0& \frac{1}{2.75}\end{bmatrix}\left ( \begin{bmatrix}4u(t)\\2u(t)\end{bmatrix}- \begin{bmatrix}9&-5\\-5&5\end{bmatrix}\begin{bmatrix}\dot{x}_1\\\dot{x}_2\end{bmatrix}-\begin{bmatrix}650&-300\\-300&300\end{bmatrix}\begin{bmatrix}{x}_1\\{x}_2\end{bmatrix}\right ) \end{split}\]

En general se puede expresar:

(24)\[\ddot{x}=M^{-1}\left (f- B\dot{x}-Kx\right )\]

De la misma manera que en el caso del sistema de un grado de libertad, se puede expresar el vector de posición como:

(25)\[x=M^{-1}\left ( \int^{t}_0\int^{\tau_1}_0f(\tau_1)d\tau_1d\tau_2-B\int^{t}_0\frac{dx(\tau_1)}{d\tau_1}d\tau_1-K\int^{t}_0\int^{\tau_1}_0x(\tau_1)d\tau_1d\tau_2\right )\]

La representación de las matrices \(M\), \(B\) y \(K\) se lleva a cabo utilizando bloques del tipo función embebida o de usuarios, el cual se obtiene en el menú de funciones definidas por el usuario de la biblioteca de bloques:

Figura 23 Menú de funciones definidas por el usuario.

Es posible incluir tres funciones definidas por usuario que contengan a las tres matrices del sistema dentro de un bloque llamado subsistema que permite agrupar un conjuto de bloques en uno sencillo para abreviar los diagramas, el diagrama de bloques del sistema de dos grados de libertad que se analiza en esta gráfica se muestra a continuación:

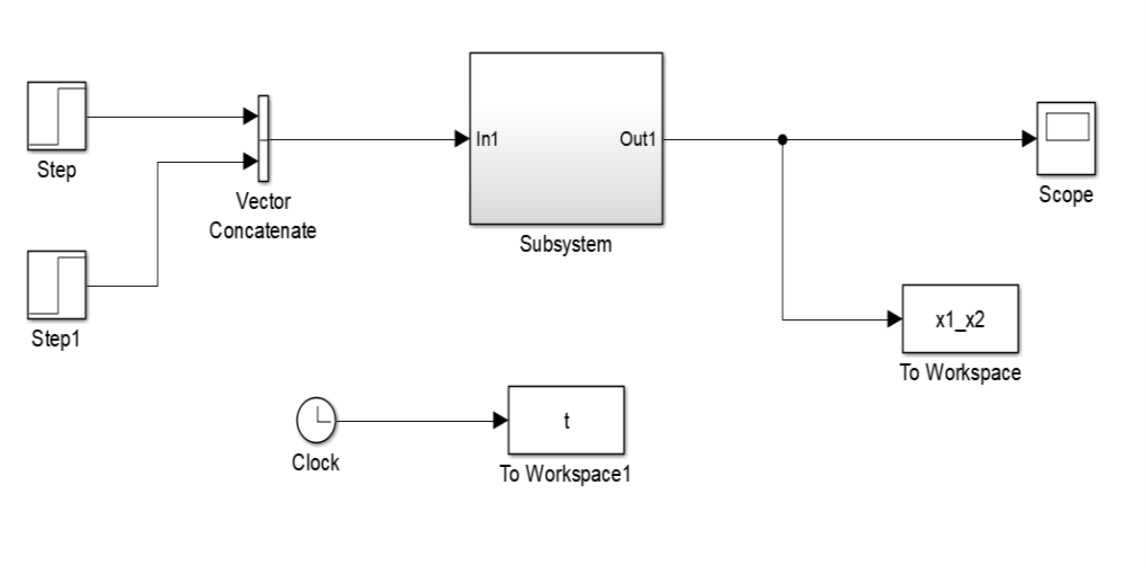
Figura 24 Diagrama de bloques del sistema.

En el que el interior del subsistema es:

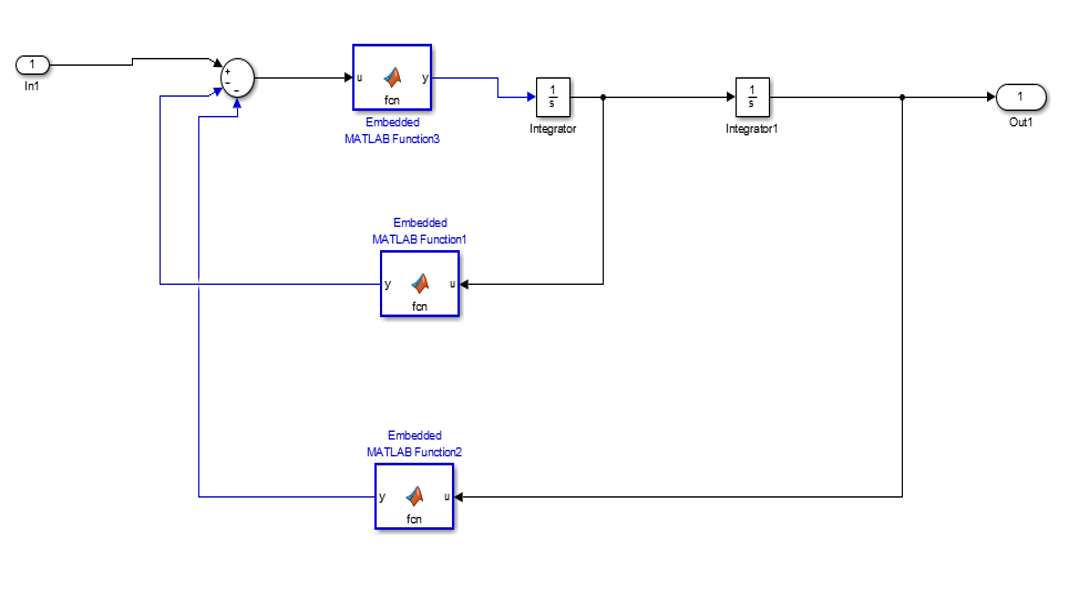
Figura 25 Diagrama de bloques interno.

Cada una de las funciones embebidas se define de manera indivudual, de manera tal que se expresa una operación en forma matricial que define la entrada y la salida, en este caso particular, la entrada es un vector de dos elementos y la salida es otro vector de dos elementos resultado de la multiplicación del vector de entrada por las matrices de masa, rigidez y amortiguamiento.

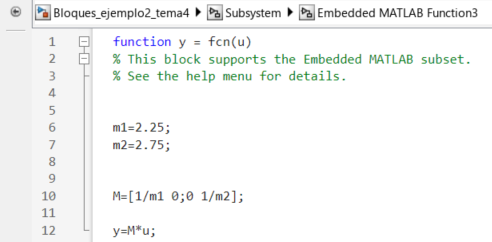
Figura 26 Código de la matriz de masas.

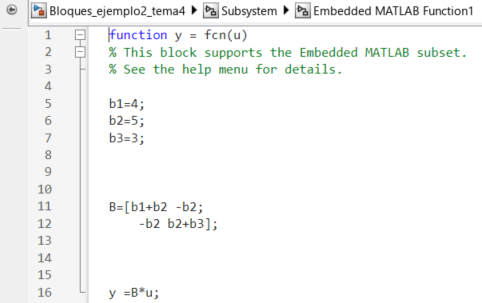
Figura 27 Código de la matriz de amortiguamiento.

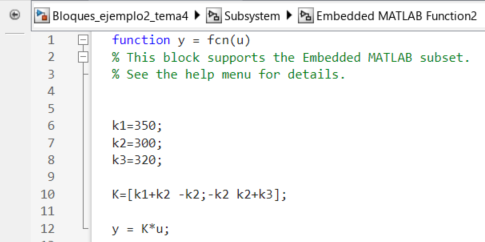
Figura 28 Código de la matriz de rigidez.

La salida de la simulación se muestra en la siguiente figura:

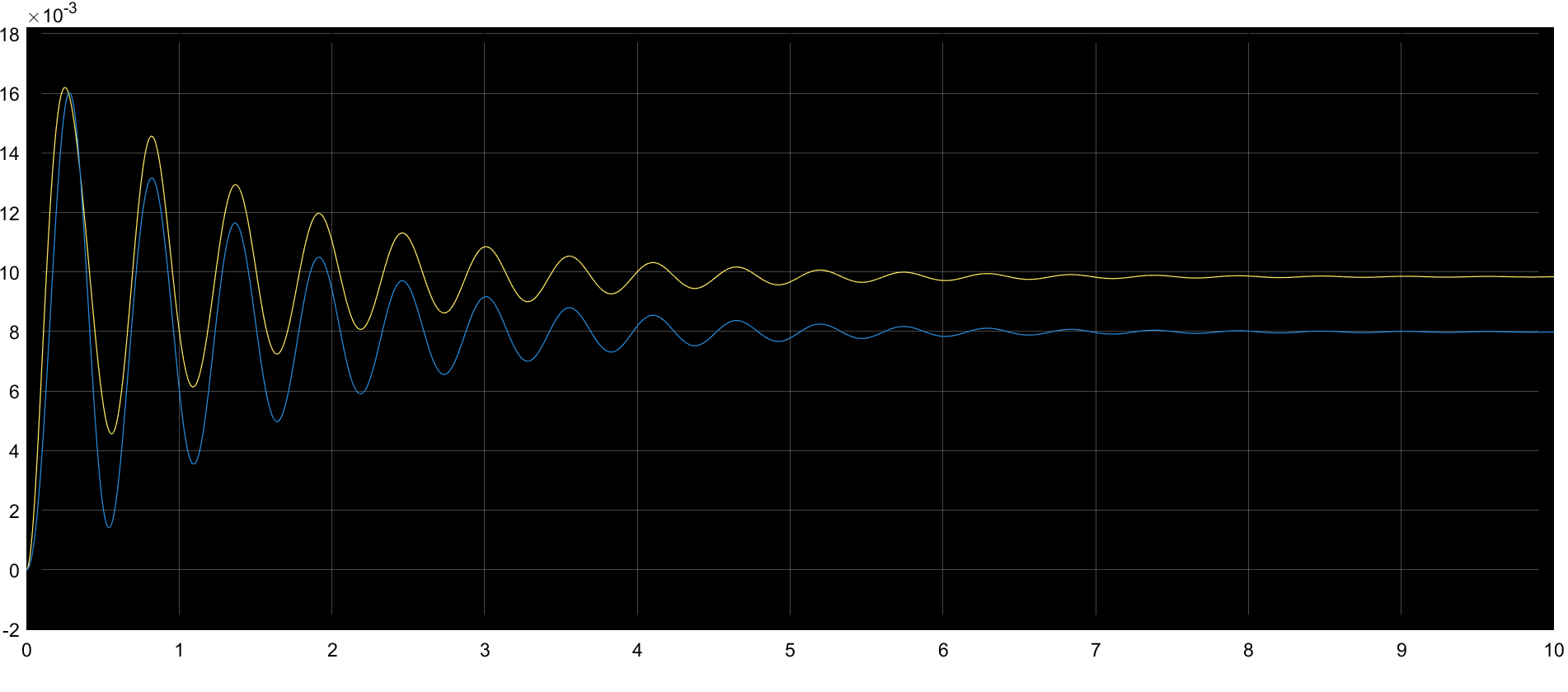
Figura 29 Salida de la simulación.

Circuito RLC de dos mallas

Un sistema similar o análogo en estructura y comportamiento al sistema analizado con anterioridad es un circuito eléctrico de dos mallas, compuesto por elementos almacen de energía como lo son las inductancias y los capacitores. Una configuración de dos grados de libertad se muestra en la Figura 30, ciertamente no es la única configuración posible para la interconexión de los componentes, sin embargo constituye un buen punto de partida para el análisis de las analogías entre sistemas mecánicos y sistemas eléctricos. En la configuración en cascada mostrada en la Figura 30 las incógnitas son las corrientes \(i_1\) e \(i_2\).

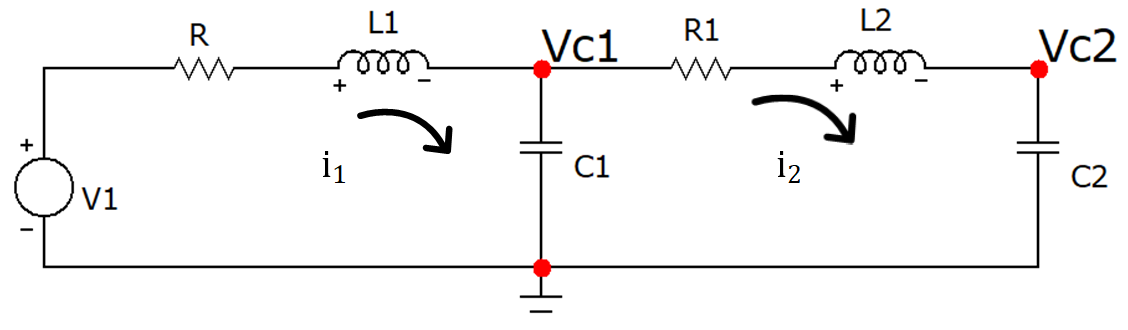
Figura 30 Circuito eléctrico de 2 mallas.

Considerando las relaciones constitutivas de los componetes:

\[ v_c=\frac{1}{C_ 1}\int{i_cdt},~~~~i_c=C\frac{dv_c}{dt},~~~~v_L=L\frac{di_L}{dt},~~~~v_R=i_RR \]

Se obtiene el sistema de ecuaciones diferenciales para las corrientes de malla \(i_1\) e \(i_2\):

(26)\[\begin{split}\begin{eqnarray} v_1=R_1i_1+L_1\frac{di_1}{dt}+\frac{1}{C_1}\int{(i_1-i_2)dt}\\ \frac{1}{C_1}\int{(i_1-i_2)dt}=R_2i_2+L_2\frac{di_2}{dt}+\frac{1}{C_2}\int{i_2dt} \end{eqnarray}\end{split}\]

Es posible agrupar el conjunto de ecuaciones (26) para obtener:

(27)\[\begin{split}\begin{eqnarray} L_1\frac{di_1}{dt}+R_1i_1+\frac{1}{C_1}\int{(i_1-i_2)dt}=v_1\\ L_2\frac{di_2}{dt}+R_2i_2-\frac{1}{C_1}\int{(i_1-i_2)dt}+\frac{1}{C_2}\int{i_2dt}=0 \end{eqnarray}\end{split}\]

Derivando con respecto al tiempo las ecuaciones (27) se obtiene:

\[ L_ 1\frac{d^2i_ 1}{dt^2}+R_ 1\frac{di_ 1}{dt}+\frac{(i_ 1-i_ 2)}{C_ 1}=\frac{dv_1}{dt} \]

\[ L_ 2\frac{d^2i_2}{dt^2}+R_ 2\frac{di_ 2}{dt}+\frac{i_2}{C_ 2}-\frac{(i_ 1-i_ 2)}{C_1}=0 \]

En forma matricial:

(28)\[\begin{equation} L\ddot{i}+R\dot{i}+Ci=\dot{v}_1 \end{equation}\]

donde:

\[\begin{split} L=\begin{bmatrix}L_1&0\\0&L_2\end{bmatrix},~~~~R=\begin{bmatrix}R_1&0\\0&R_2\end{bmatrix}~~~~C=\begin{bmatrix}\frac{1}{C_1}&-\frac{1}{C_1}\\-\frac{1}{C_1}&\frac{1}{C_1}+\frac{1}{C_2}\end{bmatrix},~~~~i=\begin{bmatrix}i_1\\i_2\end{bmatrix},~~~~v=\begin{bmatrix}v_1\\0\end{bmatrix} \end{split}\]

son las matrices de inductancia, resistencia y capacitancia respectivamente, \(i\) es el vector de corrientes de malla y \(v\) es el vector de voltajes de entrada.

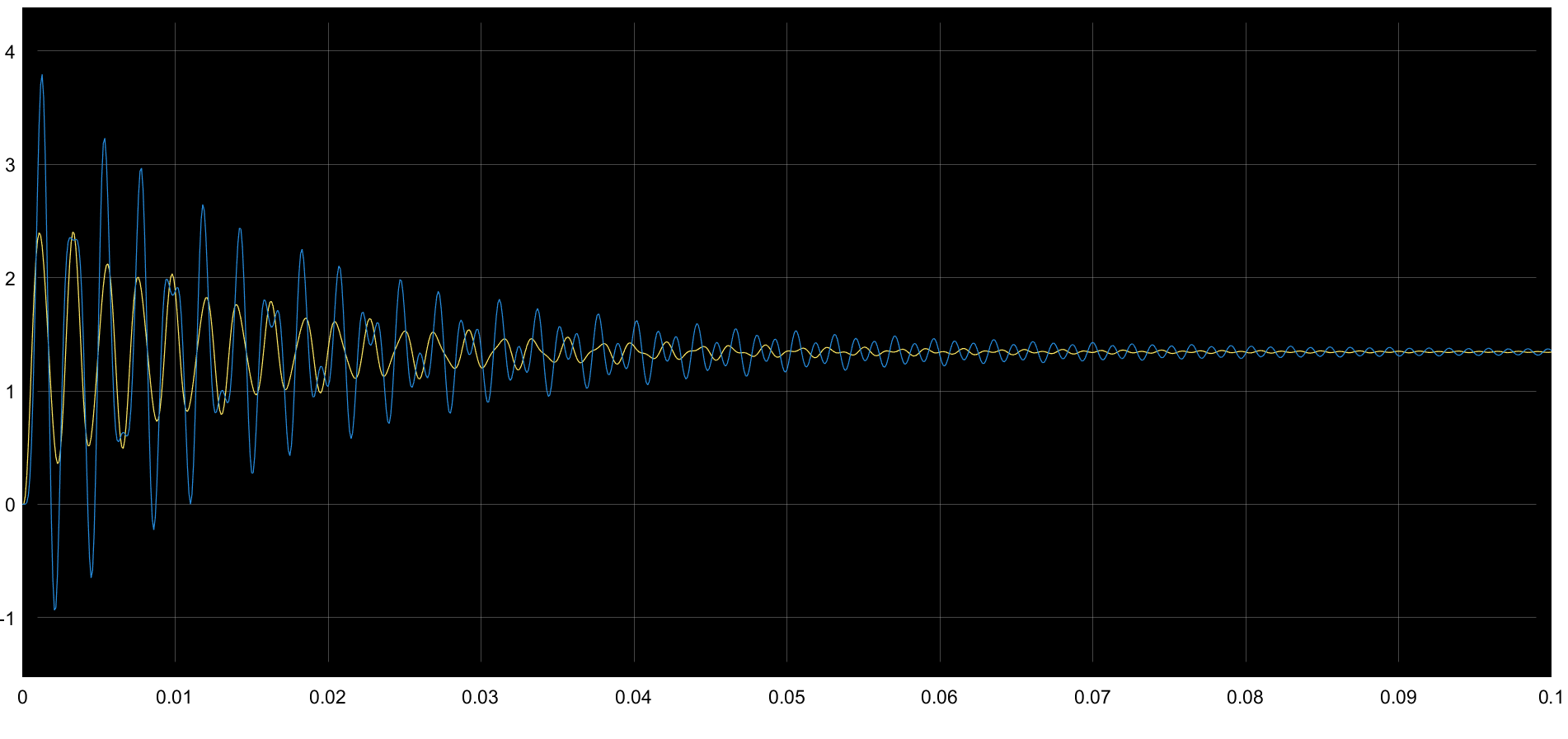
Figura 31 Salida de la simulación.

De la misma forma que en el caso del sistema mecánico, se puede expresar el vector \([i_1~~i_2]^T\) en términos de las matrices de inductancia, resistencia y capacitancia:

(29)\[\ddot{i}=L^{-1}\left (\dot{v}- R\dot{i}-Ci\right )\]

Expresando \(\ddot{i}\) en términos de las matrices \(L\), \(R\) y \(C\) e integrando dos veces se obtiene:

(30)\[i=L^{-1}\left ( \int^{t}_0\int^{\tau_1}_0\dot{v}_1(\tau_1)d\tau_1d\tau_2-R\int^{t}_0\frac{dx(\tau_1)}{d\tau_1}d\tau_1-C\int^{t}_0\int^{\tau_1}_0x(\tau_1)d\tau_1d\tau_2\right )\]

De manera tal que se puede hacer un diagrama de bloques similar al del sistema mecánico de dos grados de libertad para hacer la simulación y encontrar la solución para las corrientes \(i_1\) e \(i_2\).

Ejercicio de la práctica 15

1. Simule el sistema mecánico vibratorio que se muestra en la Figura 32, cuyos parámetros se muestran en la Tabla 18.

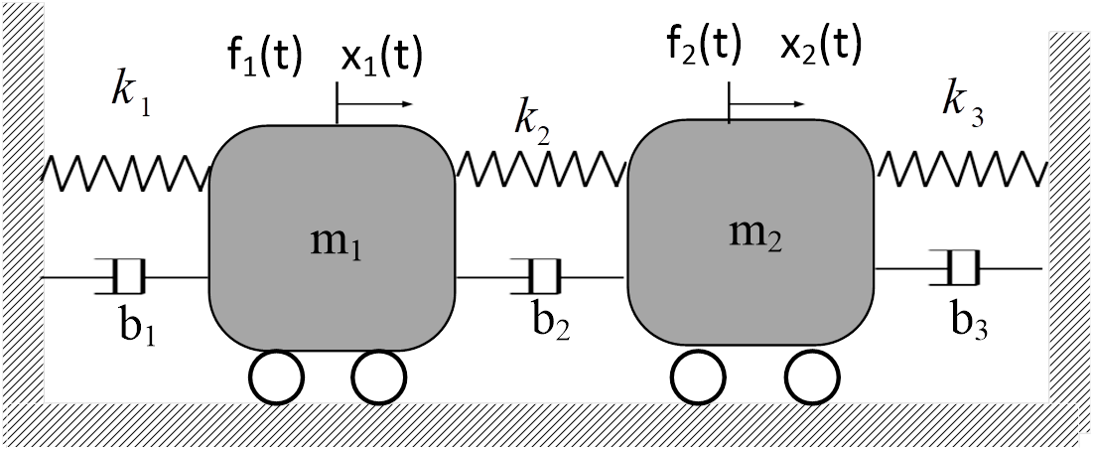
Figura 32 Sistema mecánico vibratorio de dos grados de libertad.

Tabla 18 Tabla de parámetros

\[Parámetro\]	\[Valor\]
\[m_1\]	\[1.45~[Kg]\]
\[m_2\]	\[1.75~[Kg]\]
\[b_1\]	\[5~[Ns/m]\]
\[b_2\]	\[3~[Ns/m]\]
\[b_3\]	\[1.5~[Ns/m]\]
\[k_1\]	\[450~[N/m]\]
\[k_2\]	\[330~[N/m]\]
\[k_3\]	\[430~[N/m]\]
\[f_1\]	\[4sen(2\pi t)~[N]\]
\[f_2\]	\[1.5u(t)~[N]\]

Genere la gráfica de la salidas \(x_1\) y \(x_2\) en una figura en el espacio de trabajo y guerde la imagen en formato .jpg para incluirla en el reporte.

2. Simule el circuito RLC de dos mallas que se muestra en la Figura 33 y genere la gráfica de las salidas \(i_1\) e \(i_2\) en una figura, guarde la salida en un archivo de imagen jpg. Considere \(V1=1.65u(t)~[V]\).

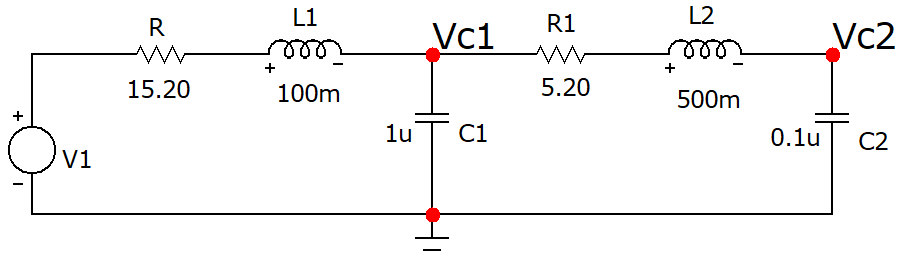
Figura 33 Circuito eléctrico de 2 mallas.