Diagramas de bode

Un diagrama de Bode es una representación gráfica de la respuesta en frecuencia de un sistema dinámico. El diagrama de bode permite una representación asintótica de la respuesta en frecuencia por medio de la consideración de los factores independientes que componen a una función de transferencia sin la necesidad de conocer de manera exacta a la transformada inversa. Los diagramas de bode se usan en el análisis y diseño de sistemas de control dada su utilidad para mostrar gráficamente la respuesta dinámica de los sistemas.

Respuesta de los sistemas a funciones sinusoides

Dado un sistema con una función de transferencia \(G(s)=\frac{N(s)}{D(s)}\), donde el grado del polinomio del numerador, o bien de la función \(N(s)\) es menor que el del denominador \(D(s)\), la respuesta \(y(t)\) de dicho sistema ante un estímulo o entrada \(x(t)=Acos(\omega_0 t)\), para \(t\geq 0\), donde \(A,\omega_0 \in \mathbb{R}\) se obtiene aplicando la transformada de Laplace:

\[ X(s)=\frac{As}{s^2+\omega_0^2} \]

Esta función de la variable compleja \(s\) se presenta como el cociente de dos polinomios que tienen raices en el plano complejo, de manera que se puede expresar:

\[ X(s)=\frac{Cs}{(s+j\omega_0)(s-j\omega_0)} \]

Donde \(j=\sqrt{-1}\), los ceros, o las raices del denominador son \(s=0\), se dice que esta función tiene un cero en el origen. En cuando a los polos o raices del denominador, estos se encuentran en \(s=\pm j\omega_0\). Dado que para la definición de función de transferencia, las condiciones iniciales son cero, la transformada de Laplace de la salida \(y(t)\), ante la entrada cosenoidal de interés es tal que:

(83)\[\begin{equation} Y(s)=\frac{AsN(s)}{D(s)(s+j\omega_0)(s-j\omega_0)} \end{equation}\]

Es posible descomponer esta última expresión en fracciones parciales:

(84)\[\begin{equation} Y(s)=\frac{\alpha(s)}{D(s)}+\frac{C}{s+j\omega_0}+\frac{C^{*}}{s-j\omega_0} \end{equation}\]

donde \(\alpha(s)\) es un polinomio en la variable compleja \(s\), \(C\) es un número complejo, o bien el residuo que se usó en secciones anteriores para calcular la expansión en fracciones parciales y la transformada inversa, \(C^*\) es el complejo conjugado. Si se multiplica la ecuación (83) por el factor \(s-j\omega_0\) y se evalúa el resultado en \(s=j\omega\) se obtiene:

\[\begin{split} \begin{eqnarray} &C=\left [ (s-j\omega_0)Y(s)\right ]_{s=j\omega_0}=\left [ \frac{CsN(s)}{D(s)(s+j\omega_0)} \right ]_{s=j\omega_0}\\ &\frac{jC\omega_0N(j\omega_0)}{D(j\omega_0)(2j\omega_0)}=\frac{C}{2}G(j\omega_0) \end{eqnarray} \end{split}\]

Si se considera la respuesta al impulso de un sistema \(h(t)\), el resultado anterior permite concluir que la transformada de Fourier de \(h(t)\), es decir \(\mathscr{F} \left \{ h(t) \right \}=H(j\omega)\) es exactamente \(H(s)|_{s=j\omega}\). Esto justifica matemáticamente el uso de la función de respuesta en frecuencia como la determinación de la salida de los sistemas ante entradas sinusoides.

Diagramas o gráficas de Bode asintóticas.

Un diagrama de bode es esencialmente una gráfica de la magnitud en decibeles dB de una función de transferencia \(G(s)\) bajo análisis. Los decibeles se definen como:

\[ |G(j\omega)|_{dB}=20log_{10}|G(j\omega)| \]

En un diagrama o gráfica de Bode también se considera la fase \(\angle |G(j\omega)|\).Tanto la magnitud como la fase de \(|G(j\omega)|\) se grafican en escala logarítmica, es decir, se grafican como una función de \(log_{10}(\omega)\). El uso de una escala de naturaleza logaritmica permite que los factores independientes que componen a una función de transferencia \(G(s)=\frac{N(s)}{D(s)}\) se pueden expresar como una suma en vez de un producto, además dado que no existe el logaritmo de un número negativo, solo se usan valores positivos de frecuencias \(\omega\). Para explicar la estructura y la aplicación de los diagramas de Bode, considere la función de transferencia expresada en la ecuación (79), la cual puede expresarse de forma alternativa y sin alterar su estructura como:

(85)\[G(s)=\frac{Y(s)}{X(s)}=K_1\frac{(1-s/z_1)(1-s/z_2)...(1-z_m)}{(1-s/p_1)(1-s/p_2)...(1-p_n)}\]

El factor constante \(K_1\) es el resultado de la factorización que permite hacer unitaria la parte constante del binomio de cada componente de la función de transferencia, tanto en el numerador como en el denominador. Al obtener la magnitud en decibeles de esta expresión, se aplica el logartimo base 10, por lo tanto:

\[\begin{split} \begin{eqnarray} |G(s)|_{dB}=20log_{10}|K_1|+20log_{10}\left |\left ( 1-\frac{j\omega}{z_1}\right )\right |&+20log_{10}\left |\left ( 1-\frac{j\omega}{z_2}\right )\right |+...+20log_{10}\left |\left ( 1-\frac{j\omega}{z_m}\right )\right |\\ -20log_{10}\left |\left ( 1-\frac{j\omega}{p_1}\right )\right |&-20log_{10}\left |\left ( 1-\frac{j\omega}{p_2}\right )\right | -...-20log_{10}\left |\left ( 1-\frac{j\omega}{p_n}\right )\right | \end{eqnarray} \end{split}\]

Mientras que la fase se obtiene como:

\[\begin{split} \begin{eqnarray} \angle |G(j\omega)|=\angle |K_1|+ \angle \left ( 1-\frac{j\omega}{z_1}\right ) +\angle \left ( 1-\frac{j\omega}{z_2}\right )+...+\angle \left ( 1-\frac{j\omega}{z_m}\right )\\ -\angle \left ( 1-\frac{j\omega}{p_1}\right )-\angle \left ( 1-\frac{j\omega}{p_2}\right )-...-\angle \left ( 1-\frac{j\omega}{p_n}\right ) \end{eqnarray} \end{split}\]

De esta manera, se puede calcular y considerar a cada uno de los factores y su contribución a la función de respuesta en frecuencia de manera individual, debido a que la operación logaritmo convierte al producto en una suma y en una resta para el caso de los factores en el denominador.

Gráfica y contribución del factor cero en el origen.

Cuando se considera el \(i\)-ésimo factor independiente que surge al considerar \(G_i(s)=s|_{s=j\omega}\), la magnitud y la fase de esta estructura particular se calcula como:

\[ 20log_{10}|G_i(j\omega)|=20log_{10}|j\omega|=20log_{10}(\omega) \]

En este caso, la fase es simplemente:

\[ \angle G_i(\omega)=\angle j\omega =90° \]

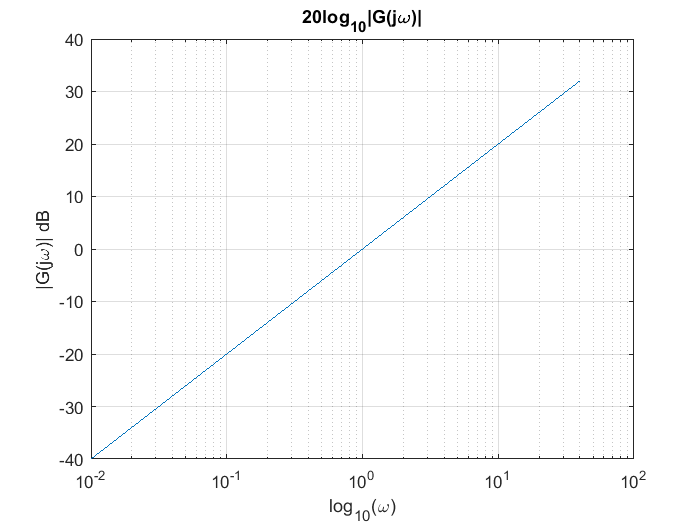
La magnitud de este factor, cuando se grafica como una función de \(log_{10}(\omega)\) es una línea recta que cruza los \(0~dB\) cuando \(\omega=1\), con una pendiente de \(20dB\) por década. Eso se demuestra con la siguiente gráfica que se obtiene usando MATLAB

clear
close all
clc

omega=[0:0.01:40];
magG=20*log10(abs(i*omega));
semilogx(omega,magG)
grid
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega)")
ylabel("|G(j\omega)| dB")

Gráfica y contribución del factor polo en el origen.

Sea ahora el \(i\)-ésimo factor independiente que surge al considerar \(G_i(s)=\frac{1}{s}|_{s=j\omega}\), la magnitud y la fase de esta estructura particular se calcula como:

\[ 20log_{10}\left |G_i(j\omega)\right|=20log_{10}\left| \frac{1}{j\omega}\right|=-20log_{10}(\omega) \]

En este caso, la fase es simplemente:

\[ \angle G_i(\omega)=\angle \left ( \frac{1}{j\omega} \right ) =-90° \]

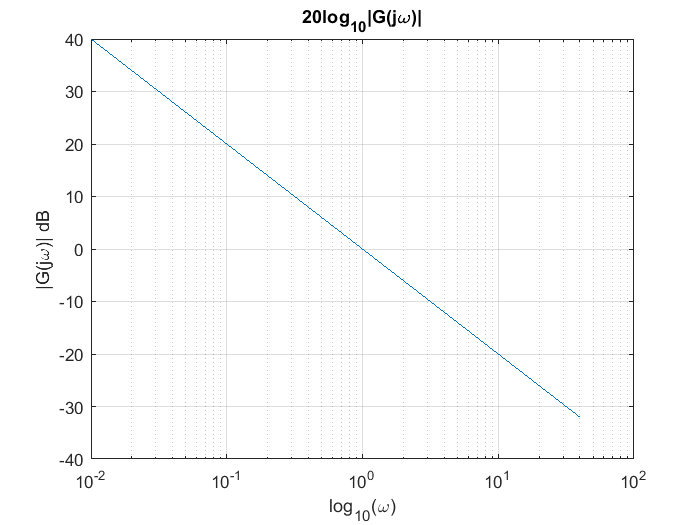
La magnitud de este factor, cuando se grafica como una función de \(log_{10}(\omega)\) es una línea recta que cruza los \(0~dB\) cuando \(\omega=1\), con una pendiente de \(20dB\) por década. Eso se demuestra con la siguiente gráfica que se obtiene usando MATLAB

clear
close all
clc

omega=[0:0.01:40];
magG=-20*log10(abs(i*omega));
semilogx(omega,magG)
grid
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega)")
ylabel("|G(j\omega)| dB")

Cero real fuera del origen.

Sea el \(i\)-ésimo factor independiente que surge al considerar \(G_i(s)=\left | 1-\frac{j\omega}{z_i} \right |_{s=j\omega}\) , la magnitud y la fase de esta estructura particular se calcula como:

\[ 20log_{10}\left |G_i(j\omega)\right|=20log_{10}\sqrt{1+\left ( \frac{\omega}{z_i}\right )^2}=10log_{10} \left [ 1+\left ( \frac{\omega}{z_i}\right )^2 \right ] \]

En este caso, la fase es:

\[ \angle G_i(\omega)=\angle \left ( 1+ \frac{j\omega}{z_i} \right ) =-tan^{-1}\left (\frac{\omega}{z_i} \right ) \]

La magnitud de este factor también se grafica como una función de \(log_{10}(\omega)\). Cuando se consideran valores de frecuencia mucho menores y mucho mayores al zero \(z_i\), es decir una década antes y una década después a \(\omega=z_i\) se aplican simplificaciones para determinar el comportamiento de las asíntotas de magnitud y fase.

Contribución de un cero en el origen:

Para el término \(G_i(j\omega)=1-j\omega/z_i\) se cumple que:

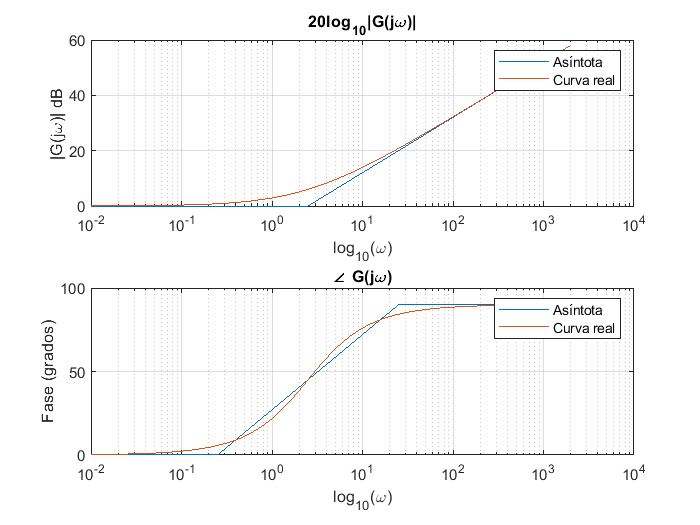
La magnitud: Es una recta con pendiente \(0\) dB cuando \(\omega<<|z_i|\) dado que la magnitud tiende asintóticamente a \(0\) dB. Para valores de \(\omega\) tales que \(\omega>>|z_i|\) la contribución es una recta con pendiente de 20dB por década, que cruza con cero dB en \(\omega=|z_i|\). En la frecuencia \(\omega=z_i\) la magnitud es de 3 dB, por lo tanto, la curva de magnitud pasa 3 dB arriba de la intersección de las asintotas de la curva aproximada.

La fase: es una recta con pendiente \(0°\) por década para valores de \(\omega<<|z_i|\). Para valores de \(\omega\) tales que \(\omega>>|z_i|\), la fase es 90° para \(z_i<0\) y -90° para \(z_i>0\). En el valor de \(\omega=z_i\) la fase es exactamente 45° para \(z_i<0\) y -45° para \(z_i>0\) (Kamen and Heck [KH07]).

Lo anterior se demuestra con la siguiente gráfica que se obtiene usando MATLAB

clear
close all
clc

omega=[0:0.01:2000];
magG=(20*(log10(omega/2.5))).*(omega>=2.5);
fase=(45)*(log10(omega/0.25)).*(omega>0.25)-(45)*(log10(omega/25)).*(omega>25);

subplot(2,1,1)
semilogx(omega,magG)
grid
hold on
semilogx(omega,20*log10(abs(1+omega/2.5)))
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega)")
ylabel("|G(j\omega)| dB")
legend("Asíntota","Curva real")

subplot(2,1,2)
semilogx(omega,fase)
hold on
semilogx(omega,(360/(2*pi))*angle((1+j*omega/2.5)))
grid
title("\angle G(j\omega)")
xlabel("log_{10}(\omega)")
ylabel("Fase (grados)")
legend("Asíntota","Curva real")

Polo real fuera del origen.

Sea el \(i\)-ésimo factor independiente que surge al considerar \(G_i(s)=\left | \frac{1}{s-\frac{j\omega}{p_i}}\right |_{s=j\omega}\), la magnitud y la fase de esta estructura particular se calcula como:

\[ 20log_{10}\left |G_i(j\omega)\right|=20log_{10}\frac{1}{\sqrt{1+\left ( \frac{\omega}{p_i}\right )^2}}=-10log_{10} \left [ 1+\left ( \frac{\omega}{p_i}\right )^2 \right ] \]

En este caso, la fase es:

\[ \angle G_i(\omega)=\angle \left ( \frac{1}{ 1+ \frac{j\omega}{p_i}} \right ) =-tan^{-1}\left (-\frac{\omega}{p_i} \right )=tan^{-1}\left (\frac{\omega}{p_i} \right ) \]

La magnitud de este factor tambien se grafica como una función de \(log_{10}(\omega)\). Cuando se consideran valores de frecuencia mucho menores y mucho mayores al polo \(p_i\), es decir una década antes y una década despues a \(\omega=p_i\) se aplican simplificaciones para determinar el comportamiento de las asíntotas de magnitud y fase.

Contribución de un polo en el origen:

Para el término \(G_i(j\omega)=\frac{1}{1-j\omega/p_i}\) se cumple que:

La magnitud: Es una recta con pendiente \(0\) dB cuando \(\omega<<|p_i|\) dado que la magnitud tiende asintóticamente a \(0\) dB. Para valores de \(\omega\) tales que \(\omega>>|p_i|\) la contribución es una recta con pendiente de -20dB por década, que cruza con cero dB en \(\omega=|p_i|\). En la frecuencia \(\omega=p_i\) la magnitud es de -3 dB, por lo tanto, la curva de magnitud pasa 3 dB por debajo de la intersección de las asintotas de la curva aproximada.

La fase: es una recta con pendiente \(0°\) por década para valores de \(\omega<<|p_i|\). Para valores de \(\omega\) tales que \(\omega>>|p_i|\), la fase es -90° para \(p_i<0\) y 90° para \(p_i>0\). En el valor de \(\omega=p_i\) la fase es exactamente -45° para \(p_i<0\) y 45° para \(p_i>0\) (Kamen and Heck [KH07]).

Lo anterior se demuestra con la siguiente gráfica que se obtiene usando MATLAB

clear
close all
clc

omega=[0:0.01:2000];
magG=(-20*(log10(omega/2.5))).*(omega>=2.5);
fase=(-45)*(log10(omega/0.25)).*(omega>0.25)+(45)*(log10(omega/25)).*(omega>25);

subplot(2,1,1)
semilogx(omega,magG)
grid
hold on
semilogx(omega,20*log10(abs(1./(1+omega/2.5))))
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega)")
ylabel("|G(j\omega)| dB")
legend("Asíntota","Curva real")

subplot(2,1,2)
semilogx(omega,fase)
hold on
semilogx(omega,(360/(2*pi))*angle(1./(1+j*omega/2.5)))
grid
title("\angle G(j\omega)")
xlabel("log_{10}(\omega)")
ylabel("Fase (grados)")
legend("Asíntota","Curva real")

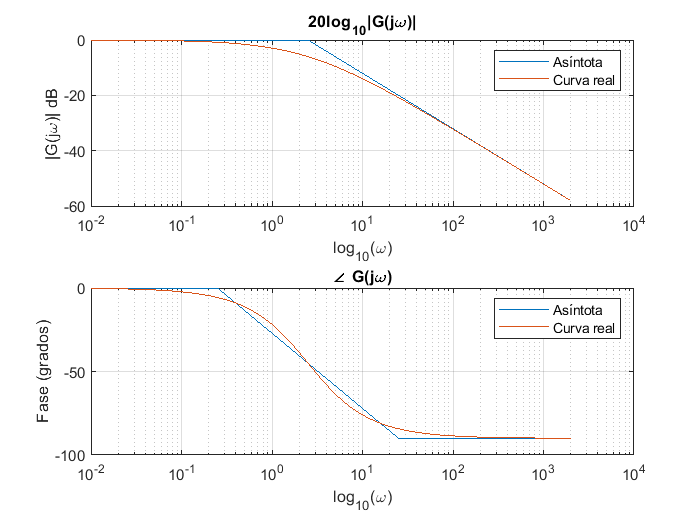
Polos con parte imaginaria o polos conjugados.

Hemos analizado sistemas en los que las raíces del polinomio característico o el denominador de la función de transferencia tiene raices de la forma \(r_{1,2}=\alpha \pm j\beta\), con \(j=\sqrt{-1}\), estos sistemas pueden considerarse como factores que son parte de un sistema más complejo. Sea el factor dado por la estructura:

\[ G(s)=\frac{1}{a_2s^2+a_1s+a_0}=\frac{p_1p_1^{*}}{(1-s/p_1)(1-s/p_1^{*})}=\frac{|p_1|^2}{(s-p_1)(s-p_1^{*})} \]

La función \(G(s)\) se puede expresar en una forma conocida que describe las características dinámicas de los sistemas, es decir, en términos de la frecuencia natural \(\omega_n\) no amortiguada y la razón de amortiguamiento \(\xi\) como sigue:

(86)\[G(s)=\frac{\omega^2_n}{s^2+2\xi\omega_n s+\omega_n^2}\]

de donde se sigue que: \(\omega_n^2=|p_1|^2\) y \(2\xi\omega_n=-2Real\{p_1\}\). Es importante mencionar, que para un sistema causal y estable, la magnitud \(Real\{p_1\}\) es negativa, mientras que el factor de amortiguamiento \(\xi\) es tal que \(0<\xi<1\) (Kamen and Heck [KH07]).

Sistemas de segundo orden.

La ecuación (86) expresa de forma muy conveniente la dinámica de los sistemas de segundo orden sin restringirse al caso sub-amortiguado, es decir, sin restringirse al caso en el que solo existe un par de polos complejos conjugados, sabemos que la parte imaginaria de un par de polos complejos conjugados se relaciona con la oscilación. Usando la ecuación (86) para el caso general en el que se tienen dos raices o polos \(p_1\) y \(p_2\) en general, es decir, pueden ser reales o complejos, se puede expresar a la función de transferencia \(G(s)\) como (Kamen and Heck [KH07]):

\[ G(s)=\frac{1}{(1-s/p_1)(1-s/p_2)}=\frac{p_1p_2}{(s-p_1)(s-p_2)} \]

Usando la esctructura general de los sistemas de segundo orden, es decir expresando \(G(s)\) en términos de la frecuencia natural y la razón de amortiguamiento, con la estructura de la ecuación (86), se pueden obtener las expresiones:

\[ \omega_n^2=p_1p_2,~~~~~~2\xi\omega_n=-Real\{p_1\}-Real\{p_1\} \]

De la misma manera que en el caso anterior, \(\omega_n\) es la frecuencia natural no amortiguada del sistema y \(\xi\) es la razón de amortiguamiento. Estos son conocidos tambien como los parámetros modales del sistema y se obienen directamente de los polos del sistema. La razón de amortiguamiento se relaciona con los polos como:

\[ \xi=\frac{-Real\{p_1\}-Real\{p_2\}}{2\sqrt{p_1p_2}} \]

Los polos, en términos de los parámetros modales se expresan como:

\[ p_{1,2}=-\xi\omega_n \pm \sqrt{\xi^2-1} \]

Clasificación de los sistemas según sus características dinámicas:

Un sistema dinámico se puede clasificar con base en su capacidad disipativa o su factor de amortiguamiento \(\xi\) y sus polos \(p_{1,2}\) como:

Sobreamortiguado: cuando tiene dos polos \(p_1\) y \(p_2\) reales y distintos. Esto implica además que el factor de amortiguamiento es tal que \(\xi>1\).

Críticamente amortiguado: cuando tiene dos polos \(p_{1,2}\) iguales o repetidos \(p_1=p_2=-\xi\omega_n\). Esto implica además que el factor de amortiguamiento es tal que \(\xi=1\).

Sub-amortiguado: cuando los polos del sistema son complejos conjugados \(p_1=\alpha \pm j\beta\) y se expresan como:

\[ p_{1,2}=-\xi\omega_n \pm j\omega_n\sqrt{1-\xi^2} \]

En el caso sub-amortiguado \(\xi<1\).

Contribución del factor de segundo orden en el diagrama de Bode.

Para determinar la contribución en forma asintótica de un factor de segundo orden, considérese la estructura de la ecuación (86):

\[ G_i(j\omega)=\left | \frac{\omega^2_n}{s^2+2\xi\omega_ns+\omega_n^2}\right|_{s=j\omega}= \frac{\omega^2_n}{(j\omega)^2+2\xi\omega_n(j\omega)+\omega_n^2}=\frac{1}{1-\left ( \frac{\omega}{\omega_n} \right )^2+2\xi j\left ( \frac{\omega}{\omega_n} \right )} \]

La magnitud en decibeles se obtiene como:

\[ 20log_{10}|G_i(j\omega)|=-10log_{10}\left ( \left ( 1-\left ( \frac{\omega}{\omega_n} \right )^2\right )^2+\left ( 2\xi j\left ( \frac{\omega}{\omega_n} \right )\right )^2 \right ) \]

La fase se calcula como:

\[ \angle G_i(\omega)=-tan^{-1}\left ( \frac{2\xi\left ( \frac{\omega}{\omega_n} \right )}{1-\left ( \frac{\omega}{\omega_n} \right )^2} \right ) \]

La magnitud de este factor también se grafica como una función de \(log_{10}(\omega)\). Cuando se consideran valores de frecuencia mucho menores y mucho mayores al polo \(p_i\), es decir una década antes y una década después a \(\omega=p_i\) se aplican simplificaciones para determinar el comportamiento de las asíntotas de magnitud y fase.

Contribución de un factor de segundo orden:

Para el término \(G_i(j\omega)= \frac{\omega^2_n}{s^2+2\xi\omega_ns+\omega_n^2}\) se considera que:

La magnitud: Es una recta con pendiente \(0\) dB cuando \(\omega<<\omega_n\) dado que la magnitud tiende asintóticamente a \(0\) dB. Para valores de \(\omega\) tales que \(\omega>>\omega_n\) la contribución es una recta con pendiente de -40dB por década, que cruza con cero dB en \(\omega=\omega_n\). En la frecuencia \(\omega=\omega_n\) la magnitud real es \(|G(j\omega_n)|=-10log_{10}(2\xi)\) dB.

La fase: es una recta con pendiente \(0°\) por década para valores de \(\omega<<\omega_n\). Para valores de \(\omega\) tales que \(\omega>>\omega_n\), la fase converge asintóticamente a -180° para \(p_i<0\). El valor de frecuencia \(\omega=\omega_n\) se conoce como frecuencia esquina, para un factor de segundo orden cuando \(\omega=\omega_n\) la fase es exactamente \(90°\) (Kamen and Heck [KH07]).

Lo anterior se demuestra con la siguiente gráfica que se obtiene usando MATLAB.

clear
close all
clc

wn=2.5;
psi=0.15;

omega=[0:0.01:2000];
magG=(-40*(log10(omega/wn))).*(omega>=wn);
fase=(-90)*(log10(omega/(wn*0.1))).*(omega>(wn*0.1))+(90)*(log10(omega/(wn*10))).*(omega>(wn*10));


subplot(2,1,1)
semilogx(omega,magG)
grid
hold on
semilogx(omega,20*log10(abs((wn^2)./((i*omega).^2+2*psi*wn*(i*omega)+wn.^2))))
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega)")
ylabel("|G(j\omega)| dB")
legend("Asíntota","Curva real")
axis([0 max(omega) -100 20])

subplot(2,1,2)
semilogx(omega,fase)
hold on
semilogx(omega,(360/(2*pi))*angle((wn^2)./((i*omega).^2+2*psi*wn*(i*omega)+wn.^2)))
grid
title("\angle G(j\omega)")
xlabel("log_{10}(\omega)")
ylabel("Fase (grados)")
legend("Asíntota","Curva real")

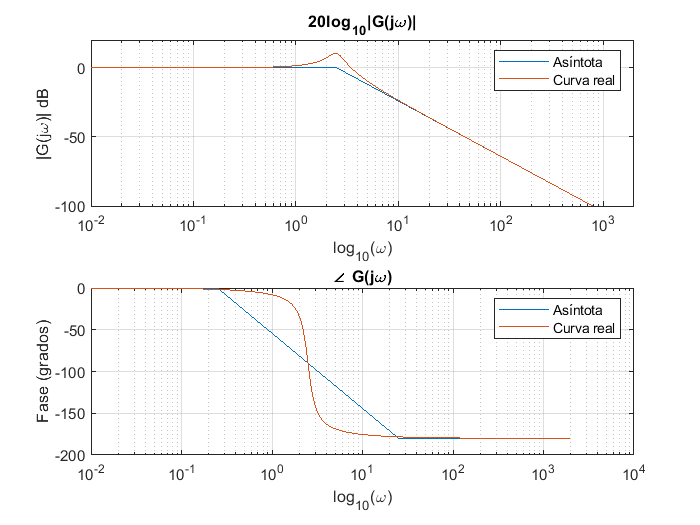
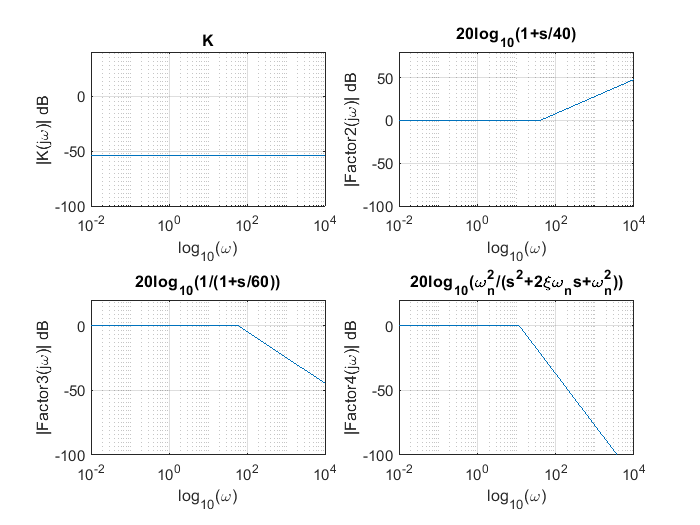
Ejemplo: diagrama de bode de una función de transferencia

Considerese el sistema cuya función de transferencia es:

\[ G(s)=\frac{(s+40)}{(s+60)(2.5s^2+3s+350)} \]

Se econtrará la gráfica de bode del sistema. Como primer paso, se expresa a la función de transferencia bajo análisis en la forma:

\[ G(s)=K\frac{(1+s/T_1)\omega_n^2}{(1+s/T_2)(s^2+2\xi\omega_ns+\omega_n^2)} \]

Donde \(T_1=40\), \(T_2=60\), \(2\xi\omega_n=\frac{3}{2.5}\) y \(\omega_n=\sqrt{\frac{350}{2.5}}\). \(K\) es una constante que se resulta de la manipulación algebraica de \(G(s)\) para llevarla a la estructura deseada, de manera que:

\[ K=\frac{40}{60\left ( \frac{350}{2.5} \right )2.5}=0.0019 \]

De manera que el primer factor es una recta de \(20log_{10}(0.0019)\) dB, es decir \(K=-54.4032\) dB.

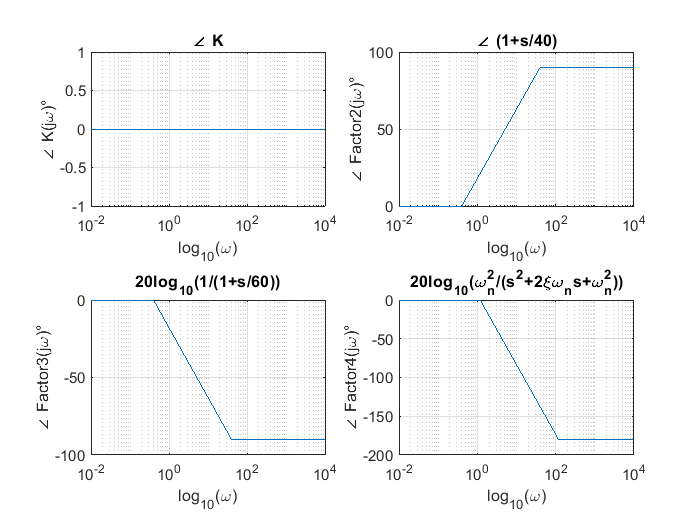
• El segundo factor \((1+s/40)\) es una recta de pendiente \(20\) dB por década con una frecuencia esquina o codo en \(\omega=40~[rad/s]\) y una aportación de \(90°\) de fase.

• El tercer factor \(\frac{1}{1+s/60}\) es una recta de pendiente \(-20\) dB por década con una frecuencia esquina en \(\omega=60~[rad/s]\), este factor aporta \(-90°\) de fase.

• Por último el cuarto factor \(\frac{\frac{350}{2.5}}{s^2+\frac{3}{2.5}s+\frac{350}{2.5}}\) es una recta de \(-40\) dB por década con una frecuencia esquina en \(\omega=\sqrt{\frac{350}{2.5}}\), con una aportación de \(-180°\) de fase.

La suma de las cuatro rectas es el diagrama de Bode del sistema bajo análisis. A continuación se muestran las gráficas de cada uno de los factores independientes, usando MATLAB.

clear
close all
clc

omega=[0:0.01:10000];

wn=sqrt(350/2.5);


K=-54.4032*ones(size(omega));
fact2=(20*(log10(omega/40))).*(omega>=40);
fase2=(45)*(log10(omega/0.40)).*(omega>0.40)-(45)*(log10(omega/40)).*(omega>40);


fact3=-20*(log10(omega/60).*(omega>=60));
fase3=(-45)*(log10(omega/0.40)).*(omega>0.40)+(45)*(log10(omega/40)).*(omega>40);


fact4=-40*(log10(omega./wn)).*(omega>=wn);
fase4=(-90)*(log10(omega./(wn*0.1))).*(omega>0.1*wn)+(90).*(log10(omega./(10*wn))).*(omega>10*wn);

subplot(2,2,1)
semilogx(omega,K)
grid
title("K")
xlabel("log_{10}(\omega)")
ylabel("|K(j\omega)| dB")
axis([0 max(omega) -100 40])

subplot(2,2,2)
semilogx(omega,fact2)
grid
title("20log_{10}|1+s/40|")
xlabel("log_{10}(\omega)")
ylabel("|Factor2(j\omega)| dB")
axis([0 max(omega) -100 80])

subplot(2,2,3)
semilogx(omega,fact3)
grid
title("20log_{10}|1/(1+s/60)|")
xlabel("log_{10}(\omega)")
ylabel("|Factor3(j\omega)| dB")
axis([0 max(omega) -100 20])

subplot(2,2,4)
semilogx(omega,fact4)
grid
title("20log_{10}|\omega_n^2/(s^2+2\xi\omega_ns+\omega_n^2)|")
xlabel("log_{10}(\omega)")
ylabel("|Factor4(j\omega)| dB")
axis([0 max(omega) -100 20])

Las fases de cada factor independiente se ilustran en las siguientes figuras:

figure
subplot(2,2,1)
semilogx(omega,zeros(size(omega)))
grid
title("\angle K")
xlabel("log_{10}(\omega)")
ylabel("\angle K(j\omega)°")

subplot(2,2,2)
semilogx(omega,fase2)
grid
title("\angle |1+s/40|")
xlabel("log_{10}(\omega)")
ylabel("\angle Factor2(j\omega)°")

subplot(2,2,3)
semilogx(omega,fase3)
grid
title("20log_{10}|1/(1+s/40)|")
xlabel("log_{10}(\omega)")
ylabel("\angle Factor3(j\omega)°")

subplot(2,2,4)
semilogx(omega,fase4)
grid
title("20log_{10}|\omega_n^2/(s^2+2\xi\omega_ns+\omega_n^2)|")
xlabel("log_{10}(\omega)")
ylabel("\angle Factor4(j\omega)°")

La gráfica asintótica de Bode final es la suma de las curvas anteriores, tanto en magnitud como en fase, en concreto, la obtención de la gráfica de bode consiste en sumar todas las pendientes de cada uno de los factores.

bodeG=K+fact2+fact3+fact4;
faseG=fase2+fase3+fase4;

figure 

semilogx(omega,bodeG)
hold on
grid
title("20log_{10}|G(j\omega)|")
xlabel("log_{10}(\omega) [rad/s]")
ylabel("|G(j\omega)| dB")
%ylabel("\angle G(j\omega)°")
axis([0 max(omega) -100 -20])
s=i*omega;
Gs=(s+40)./((s+60).*(2.5*s.^2+3*s+350));
magG=20*log10(abs(Gs));
semilogx(omega,magG)
legend("Asíntota","Curva real")

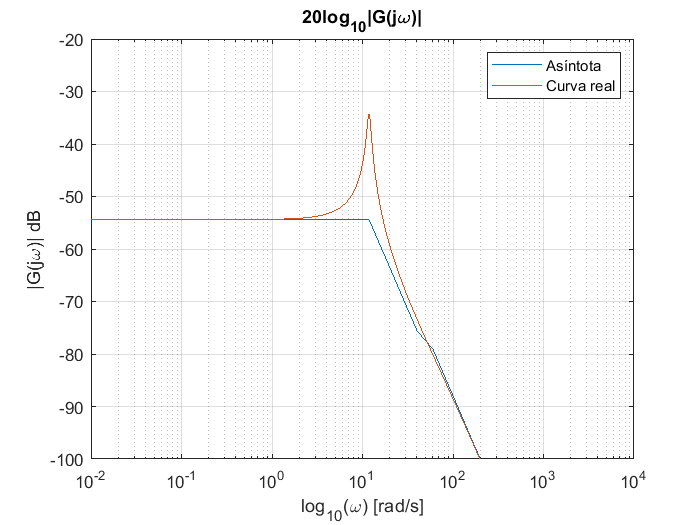
El comportamiento asintótico de la fase se obtiene también sumando las pendientes de las aportaciones en fase de los componentes individuales:

figure
semilogx(omega,faseG)
hold on
grid
title("\angle G(j\omega)")
xlabel("log_{10}(\omega) [rad/s]")
ylabel("\angle G(j\omega)°")
s=i*omega;
Gs=(s+40)./((s+60).*(2.5*s.^2+3*s+350));
magG=20*log10(abs(Gs));
semilogx(omega,(360/(2*pi))*angle(Gs))
legend("Asíntota","Curva real")
axis([0 max(omega) -200 15])

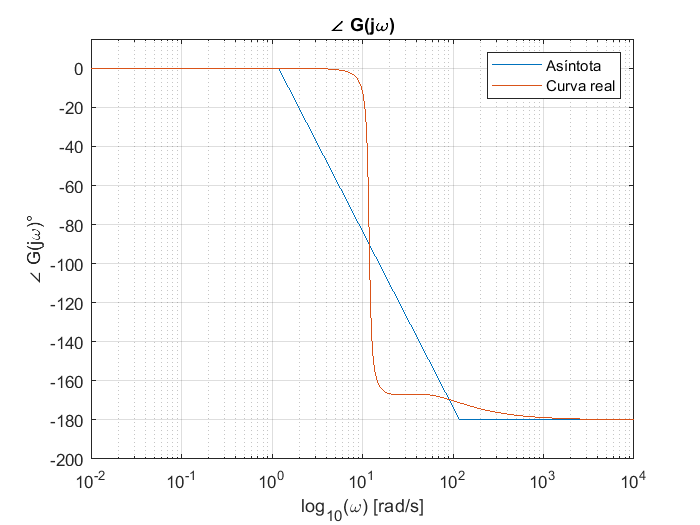
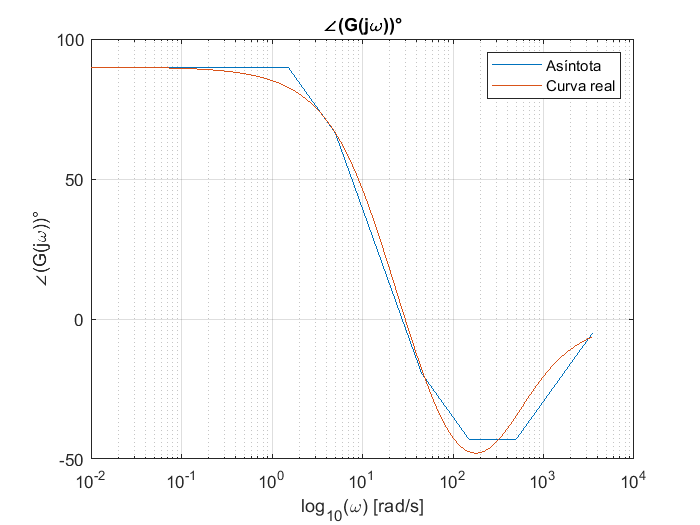
Un ultimo ejemplo ilustrará el uso MATLAB para le generación de diagramas de Bode de forma automática e intuitiva. El comando bode(G) permite generar gráficas de Bode en escala logarítmica o lineal. Por ejemplo, para la función de transferencia:

\[ G(s)=\frac{s(s+450)}{(s+15)(s+50)} \]

clear
clc
close all

w=[0:0.01:3500];
num=conv([1 0],[1 450]);
den=conv([1 15],[1 50]);
G=tf(num,den)

[mag,phase,wout]=bode(G,w);
k=20*log10(450/(15*50));

fact1=20*log10(w);

fact2=20*(log10(w/450).*(w>=450));
fase2=45*(log10(w/(45))).*(w>=(45))-45*(log10(w/(4500))).*(w>=(4500));

fact3=-20*(log10(w/15).*(w>=15));
fase3=-45*(log10(w/1.5)).*(w>=1.5)+45*(log10(w/150)).*(w>=150);

fact4=-20*(log10(w/50).*(w>=50));
fase4=-45*(log10(w/5)).*(w>=5)+45*(log10(w/500)).*(w>=500);

faseB=90+fase2+fase3+fase4;

semilogx(w,k+fact1+fact2+fact3+fact4)
hold on
grid
amp=[];
for i=1:1:max(size(mag))
amp(i)=20*log10(mag(1,1,i));
fase(i)=phase(1,1,i);
end 

semilogx(wout,amp)
title("\angle G(j\omega)|")
xlabel("log_{10}(\omega) [rad/s]")
ylabel("|G(j\omega)| dB")
legend("Asíntota","Curva real")
axis([0 max(w) -50 30])

G =
 
    s^2 + 450 s
  ----------------
  s^2 + 65 s + 750
 
Continuous-time transfer function.

La fase se obtiene de la misma manera y se compara con la curva asintótica.

figure

semilogx(wout,faseB)
hold on 
semilogx(wout,fase)

title("\angle(G(j\omega))°")
xlabel("log_{10}(\omega) [rad/s]")
ylabel("\angle(G(j\omega))°")
legend("Asíntota","Curva real")
%axis([0 max(w) -50 30])
grid