Otras definiciones y propiedades de las señales

Señales determinísticas y aleatorias

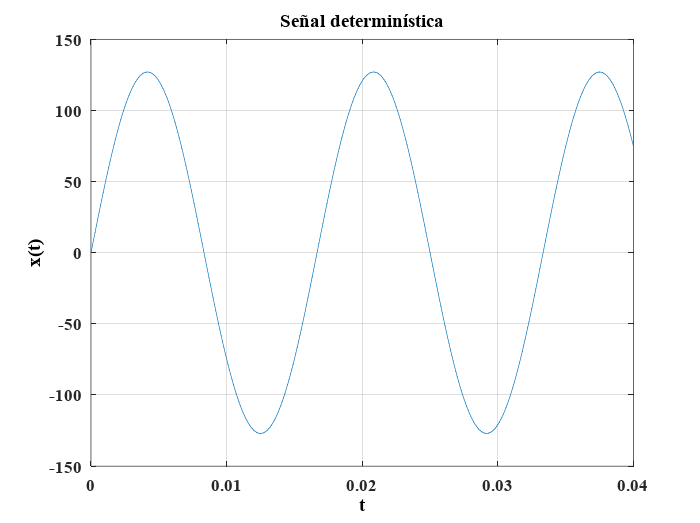
Como hemos visto, las señales describen la evolución en el tiempo de alguna variable física presente en un sistema, sea esta variable una entrada o salida al sistema. Las señales que tienen un modelo matemático en forma cerrada o aproximada se denominan señales determinísticas, dado que es posible predecir por completo su comportamiento en cualquier instante de tiempo \(t\). Un ejemplo claro es la señal que modela al voltaje de alimentación doméstico de 127 volts RMS de amplitud y 60 Hz de frecuencia.

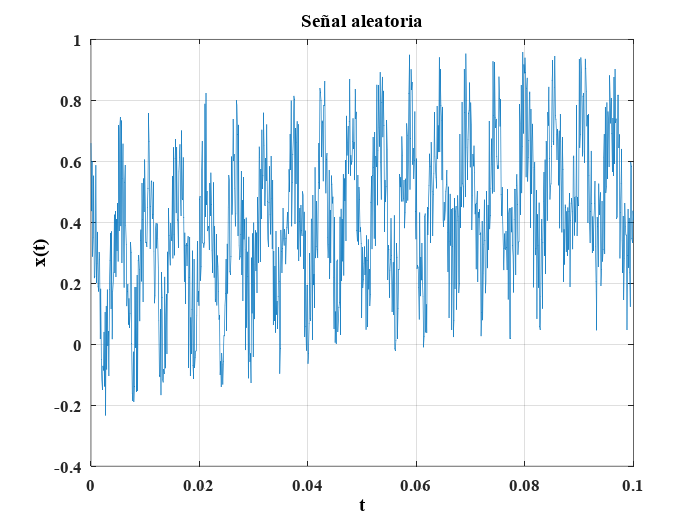
Una señal aleatoria por su parte es aquella que no tiene un modelo matemático en forma cerrada por ejemplo la señal de un micrófono en un sistema de audio o la aceleración de la tierra durante un sismo. Dado que muchas de las señales que se encuentran en los fenómenos físicos presentes en la ingeniería, es importante contar con un método que permita estudiar o comprender este tipo de señales, a menudo se utilizan parámetros estadísticos como los valores promedio y distribuciones probabilísticas. A continuación se definen dos propiedades para el análisis y caracterización de las señales.

Potencia y energía en señales

La energía de una señal se define como [Alk14]:

(8)\[\begin{equation} E_x=\int^{\infty}_{-\infty} x^2(t) dt \end{equation}\]

La ecuación (8) también se expresa como

(9)\[\begin{equation} E_x=\int^{\infty}_{-\infty} |x(t)|^2 dt \end{equation}\]

donde \(|x(t)|\) es la magnitud en el caso de funciones complejas.

La operación de promediación

La definición matemática de la operación de promediado en el tiempo de una señal es [Alk14]:

(10)\[\begin{equation} \langle x(t) \rangle = \frac{1}{T_0}\int^{\frac{T_0}{2}}_{-\frac{T_0}{2}} x(t) dt \end{equation}\]

donde se asume que \(x(t)\) es una función periódica con periodo \(T_0\). Para señales no periódicas, la ecuación (10) se convierte en:

(11)\[\begin{equation} \langle x(t) \rangle = \lim_{T\to\infty} \left [ \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}} x(t) dt \right ] \end{equation}\]

Potencia de una señal

La potencia de una señal periódica se calcula usando la expresión:

(12)\[\begin{equation} P_x= \frac{1}{T_0}\int^{\frac{T_0}{2}}_{-\frac{T_0}{2}} x^2(t) dt \end{equation}\]

para señales en la variable compleja:

(13)\[\begin{equation} P_x= \lim_{T\to\infty} \left [ \frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}} |x(t)|^2 dt \right ] \end{equation}\]

Señales de energía y señales de potencia

• Las señales de energía son aquellas que tienen energía finita y potencia cero, es decir: \(E_x<\infty\) y \(P_x=0\)

• Las señales de potencia son aquellas que tienen potencia finita y energía infinita, es decir: \(P_x<\infty\) y \(E_x \to \infty\) [Alk14]

El valor RMS de las señales

En sistemas eléctricos y electrónicos, es muy común usar el parámetro conocido como raíz cuadrada media o root-mean-square por sus sigrlas en inglés. El valor RMS se una señal \(x(t)\) se define como [Alk14]:

(14)\[\begin{equation} X_{RMS}= \sqrt{\frac{1}{T_0}\int^{\frac{T_0}{2}}_{-\frac{T_0}{2}} x^2(t) dt} = \left [ \langle x^2(t) \rangle \right ]^{\frac{1}{2}} \end{equation}\]

Un ejemplo de aplicación muy común es el cálculo del valor RMS de una señal sinusoide. Por ejemplo, el valor RMS de una señal definida como \(x(t)=Asen(\omega t+\theta)\) se obtiene usando la ecuación (14)

\[ X_{RMS}=\sqrt{\frac{1}{T_0}\int^{\frac{T_0}{2}}_{-\frac{T_0}{2}} x^2(t) dt}=\sqrt{\omega\int^{\frac{1}{2\omega}}_{-\frac{1}{2\omega}} (sen(\omega t+\theta))^2 dt} \]

Usando la identidad trigonométrica \((Asen(a))^2=\frac{A^2}{2}-\frac{A^2}{2}cos(2a)\) y considerando que \(T_0=\frac{1}{\omega_0}\), se obtiene:

\[ X_{RMS}=\sqrt{\omega\int^{\frac{1}{2\omega}}_{-\frac{1}{2\omega}}\frac{1}{2}-\frac{1}{2}cos(2\theta) dt}=\sqrt{\omega\int^{\frac{1}{2\omega}}_{-\frac{1}{2\omega}}\frac{A^2}{2}dt-\omega\int^{\frac{1}{2\omega}}_{-\frac{1}{2\omega}}\frac{A^2}{2}cos(2\omega+2\theta) dt} \]

Esta última expresión se simplifica considerando que \(\omega\int^{\frac{1}{2\omega}}_{-\frac{1}{2\omega}}\frac{A^2}{2}cos(2\omega+2\theta) dt=0\), dado que se calcula la integral del coseno en dos periodos completos, por lo tanto, el valor RMS de la sinusoide considerada es:

\[ X_{RMS}=\frac{A}{\sqrt{2}} \]

Note que el valor RMS de una señal sinusoide no depende de otro parámetro que no sea su amplitud pico.

Simetría par e impar

Simetría par

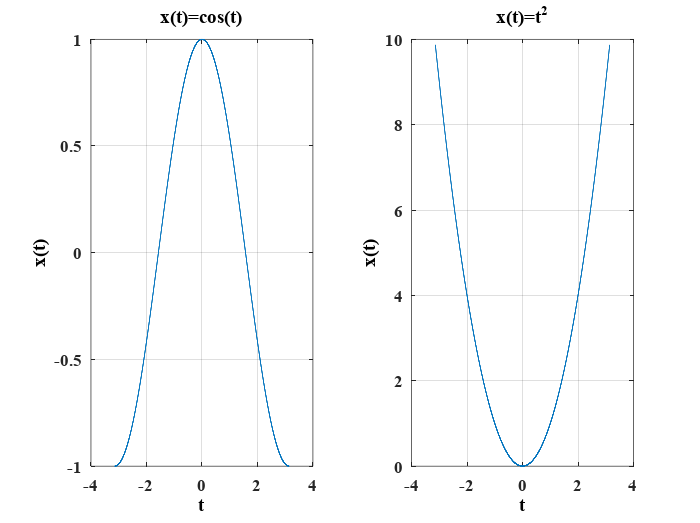
Una señal valuada en los reales tiene simetría par si se cumple que \(x(t)=x(-t)\), por ejemplo las funciones \(x(t)=cos(t)\) y \(x(t)=t^2\)

Simetría impar

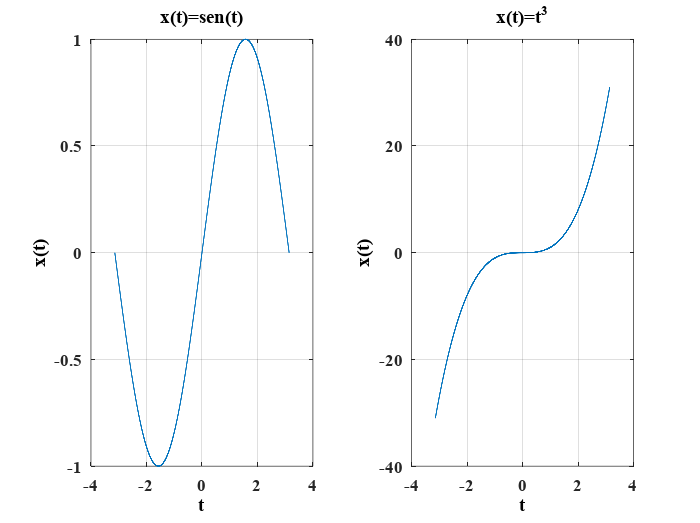
Una señal valuada en los reales tiene simetría impar si se cumple que \(x(-t)=-x(t)\), por ejemplo las funciones \(x(t)=sen(t)\) y \(x(t)=t^3\)