Modelado matemático de señales y su representación.

Contenido

Modelado matemático de señales y su representación.#

Hemos visto que las señales representan la evolución en el tiempo de una variable de interés en un sistema. Esta evolución en el tiempo se representa usando funciones que involucran expresiones matemáticas en forma cerrada, aunque cabe aclarar que no siempre existe una función en concreto o un conjunto de funciones que combinadas representen de manera fiel a una señal experimental. Cuando se trata con señales se busca principalmente lograr objetivos como:

Predecir el comportamiento de una señal, dadas sus características, es decir, al tener la forma cerrada de la expresión que modela su evolución en el tiempo, conocer de forma precisa su magnitud en determinado instante de tiempo. Esto se conoce como modelado matemático de señales.
Entender las características principales de una señal en términos de parámetros intrínsecos que la definen como lo son el contenido frecuencial o armónico, su amplitud y sus cambios característicos en el tiempo. A esto se le conoce como análisis de señales.
Crear una expresión para generar una señal con características deseadas o bien, con especificaciones de diseño, es decir, crear o construir una señal para lograr un objetivo específico, como lo es por ejemplo, proporcionar una entrada de prueba a un sistema bajo análisis o para fines de calibración. A este proceso se le conoce como síntesis de señales.

En éste último aspecto se encuentra encerrada la función principal de las señales en el contexto de este curso. El estímulo que produce una salida al interactuar con un sistema se denomina la señal de entrada al sistema y la respuesta de éste último a dicho estímulo se considera la salida del sistema. Para fines de simulación o representación numérica del comportamiento de los sistemas se trabaja con el modelo matemático de los sistemas y de las señales involucradas en su respuesta o interacción con los elementos que lo rodean.

Modelo matemático de una señal

El modelo matemático de una señal es aquella formula o expresión matemática que describe, en forma aproximada las variaciones o evolución en el tiempo de una variable física ([Alk14]).

Modelo matemático de una señal de tiempo contínuo#

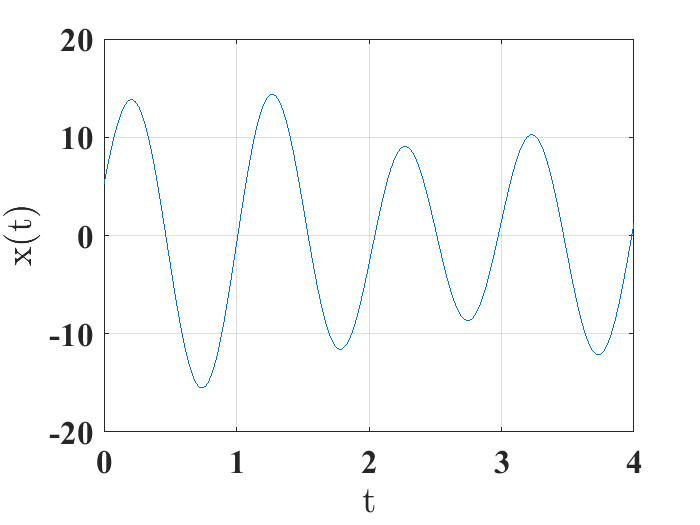
Dada una señal $x(t)$, una función que aproxima el comportamiento de una cantidad física en cada instante de tiempo $t$. En esta relación entre la variable independiente $t$ y la función $x(t)$, la señal se denomina de tiempo continuo o señal analógica. Por ejemplo la representación usando MATLAB de la señal: $$ x(t)=11.25sen(2\pi t)+5.25e^{-0.25t}cos(4.5t) $$

Se obtiene usando las líneas de código:

_images/55c36d10de82bdd16b6a36c8c5bf0d80b772c0a2962f37f534bb5bfdbfa353f2.png

Operaciones con señales#

Las señales, al ser funciones del tiempo, son compatibles con operaciones aritméticas comunes, como lo son la suma, la resta, la multiplicación y la división. Además, existen otras operaciones matemáticas que se puede aplicar a las señales como veremos más adelante como lo son el desplazamiento en el tiempo, el escalamiento en el tiempo y la inversión del vector de tiempo.

Operaciones aritméticas#

Adición de una constante#

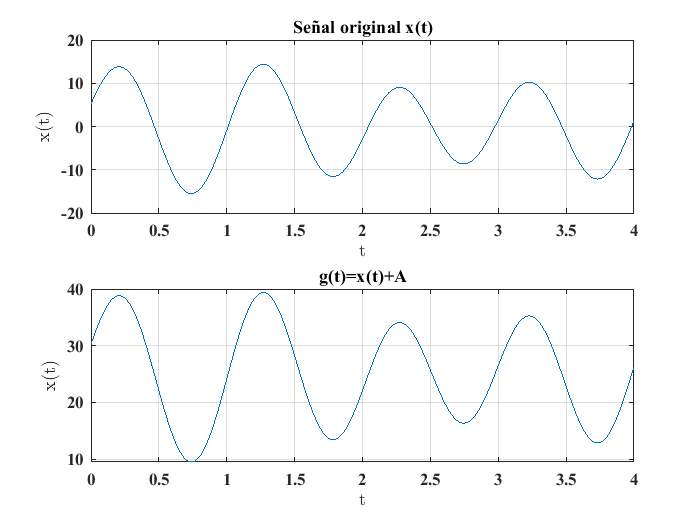
La primera operación a considerar es la adición de una constante $A$ a una señal, esta constante se conoce como offset. La expresión para esta operación es:

\[ g(t)=x(t)+A \]

donde la señal $g(t)$ es la que resulta de aplicar la operación de adición de una constante a la señal original. Lo anterior se ejemplifica usando el código:

A=25;
g_t=x(t)+A;

subplot(2,1,1)
plot(t,x(t))
grid
title("Señal original x(t)")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','x(t)',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

subplot(2,1,2)
plot(t,g_t)
grid
title("g(t)=x(t)+A")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','x(t)',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

_images/eaec07d2df32b85369bbdd11e772b7113db1297db232ff4c115da172f6b6a0dd.png

Suma de dos señales#

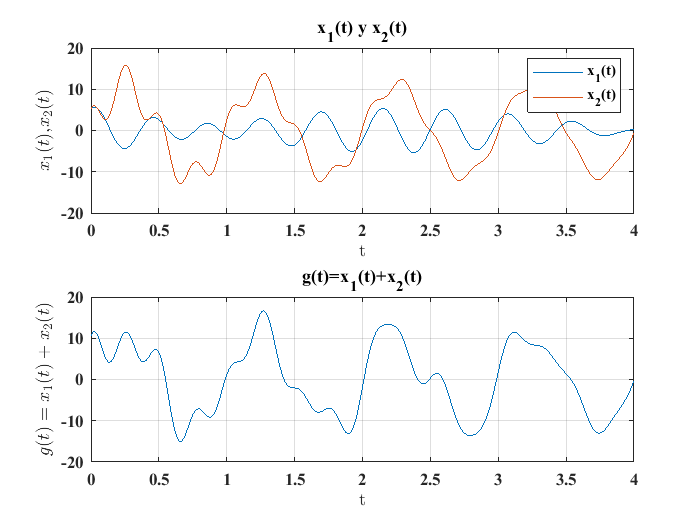
Dadas dos señales $x_1(t)$ y $x_2(t)$, se obtiene una señal $g(t)$ al sumar ambas señales individuales, esta operación significa sumar el valor de cada una de las dos señales en cada instante de tiempo $t$:

clear
close all
t = [0:0.01:4];
x1 = @(t) 2.5*sin(4*pi*t)+5.25*exp(-0.25*t).*cos(14.5*t);
x2 = @(t) 11.25*sin(2*pi*t)+5.25*exp(-0.5*t).*cos(24.5*t);

g_t=x1(t)+x2(t);

subplot(2,1,1)
plot(t,x1(t))
hold on
plot(t,x2(t))
grid
title("x_1(t) y x_2(t)")
legend("x_1(t)","x_2(t)")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1(t)$,$x_2(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 


subplot(2,1,2)
plot(t,g_t)
grid
title("g(t)=x_1(t)+x_2(t)")

 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g(t)=x_1(t)+x_2(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

_images/f939b37b574dcfb033ffa6e51ffb9413ed37efdd65e66c4ba809ef1d79539a91.png

Modelado de señales definidas a pedazos#

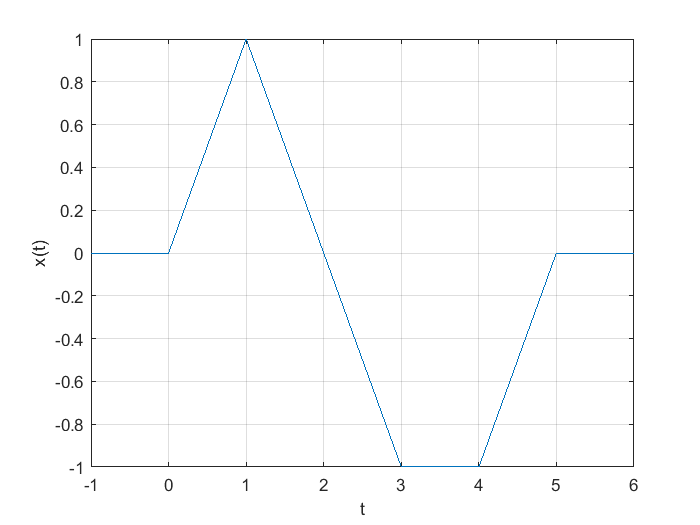
Se dice que una señal es definida a pedazos si es continua en un intervalo dado si está definida en ese intervalo y además, las expresiones matemáticas que describen o modelan a dicha señal son funciones son continuas en ese intervalo. Adicionalmente, se cumple que no hay discontinuidad en ningún punto extremo de los subintervalos. Una función continua a pedazos se define por medio de un conjunto de expresiones, utilizando una llave, funciones locales e intervalos. Por ejemplo, considere la función continua a pedazos definida en la siguiente expresión:

(1)#\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} t & si & 0 \leq t \leq 1 \\ \\ -(t-2) & si & 1 < t \leq 3 \\ \\ -1 & si & 3 < t < 4 \\ \\ t-5 & si & 4< t \leq 5 \end{array} \right. \end{equation}\end{split}\]

Como puede observarse, los subintervalos se pueden definir en MATLAB:

figure
t=[-1:0.01:6];
x=@(t) t.*((t>=0)&(t<=1))-(t-2).*((t>1)&(t<=3))-((t>3)&(t<=4))+(t-5).*((t>4)&(t<=5));

plot(t,x(t));
xlabel("t");
ylabel("x(t)")
grid;

_images/966e24cced586198107f7a62482fe91e4bf2f8a7ceae5dd1be828be458e2d149.png

Ejercicio#

Encuentre las funciones:

\[\begin{split} \begin{eqnarray} g_1(t)=1.5x(t)-1\\ g_2(t)=-1.3x(t)+2 \end{eqnarray} \end{split}\]

Encuentre las funciones

\[\begin{split} \begin{eqnarray} g_3(t)=1.5x_2(t)-1\\ g_4(t)=-1.3x_2(t)+2x(t) \end{eqnarray} \end{split}\]

para $x_2(t)$ definida como:

(2)#\[\begin{split}\begin{equation} x_2(t)= \left\{ \begin{array}{lcc} 5 & si & 0 \leq t \leq 2 \\ \\ t^2-t+10 & si & 2 < t \leq 5 \\ \\ -4t-15 & si & 5 < t < 7 \\ \\ 0 & si & 7 \leq t \end{array} \right. \end{equation}\end{split}\]

Suma de dos funciones continuas a pedazos#

Para hacer la suma de dos o mas funciones continuas a pedazos se opta por la representación usando llaves de las funciones. Si se tienen las gráficas de las señales, se obtiene el modelo de las señales a partir de las gráficas de las funciones. Para ilustrar esto, considérense las funciones $x_1(t)$ y $x_2(t)$ definidas por las gráficas:

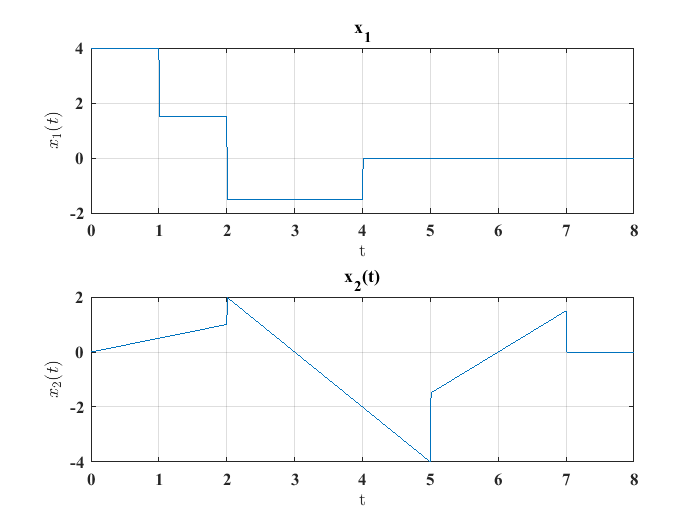
_images/bd8cbe0cf6b111169ae0ae0bb5b6daeb91db05ecb27623c9f2714a807bbd5c28.png

De acuerdo con las gráficas mostradas, los modelos matemáticos de las señales $x_1(t)$ y $x_2(t)$ son:

(3)#\[\begin{split}\begin{equation} x_1(t)= \left\{ \begin{array}{lcc} 4 & si & 0 \leq t \leq 1 \\ \\ 1.5 & si & 1 < t \leq 2 \\ \\ -1.5 & si & 2 < t < 4 \\ \\ 0 & si & 4 \leq t \end{array} \right. \end{equation}\end{split}\]

En cuanto a la señal $x_2(t)$, esta se define como:

(4)#\[\begin{split}\begin{equation} x_2(t)= \left\{ \begin{array}{lcc} 0.5t & si & 0 \leq t \leq 2 \\ \\ -2(t-3) & si & 2 < t \leq 5 \\ \\ 1.5(t-6) & si & 5 < t < 7 \\ \\ 0 & si & 7 \leq t \end{array} \right. \end{equation}\end{split}\]

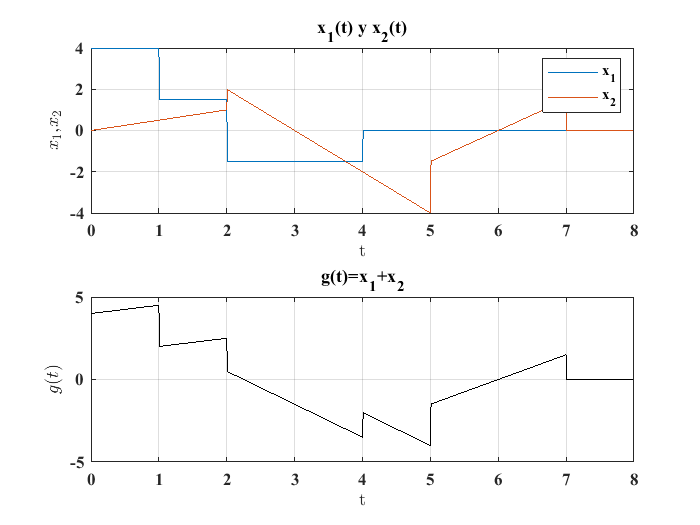
La suma de las señales $x_1$ y $x_2$ resulta en una tercera función $g(t)$ que se puede construir considerando el valor de la función en cada segmento como a continuación se describe:

\[\begin{split} \begin{equation} g(t)=x_1(t)+\textcolor{red}{x_2(t)}= \left\{ \begin{array}{lcc} 4+\textcolor{red}{0.5t} & si & 0 \leq t \leq 1 \\ \\ 1.5+\textcolor{red}{0.5t} & si & 1 < t \leq 2 \\ \\ -1.5-\textcolor{red}{2(t-3)} & si & 2 < t < 4 \\ \\ 0-\textcolor{red}{2(t-3)} & si & 4 \leq t < 5 \\ \\ \textcolor{red}{1.5(t-6)} & si & 5 \leq t < 7 \\ \\ \textcolor{red}{0} & si & 7 \leq t \end{array} \right. \end{equation} \end{split}\]

la gráfica de $g(t)$ se obtiene usando MATLAB con el código siguiente:

clear
close all
t = [0:0.01:8];
x1 = @(t)  4*((t>=0)&(t<=1))+1.5*((t>1)&(t<=2))-1.5*((t>2)&(t<=4));
x2 = @(t)  0.5*t.*((t>=0)&(t<=2))-2*(t-3).*((t>2)&(t<=5))+1.5*(t-6).*((t>5)&(t<=7));

g_t=x1(t)+x2(t);

subplot(2,1,1)
plot(t,x1(t))
grid
hold on
plot(t,x2(t))
title("x_1(t) y x_2(t)")
legend("x_1","x_2")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1$,$x_2$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

g=x1(t)+x2(t);

subplot(2,1,2)
plot(t,g,"k")
grid
title("g(t)=x_1+x_2")

 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

_images/c54f2bf03f779a9eea93e8077964fb9661fca707c7ed13b8f7f7ec611f8a9f60.png

Ejercicio 1#

Obtenga $g_2(t)=x_1x_2$

Operación de desplazamiento en el tiempo#

Una versión, desplazada en el tiempo de una señal dada $x(t)$ se obtiene si se considera la expresión:

\[ g(t)=x(t-tr) \]

donde $t_r$ es un número positivo o negativo. Lo anterior se muestra en la siguiente figura:

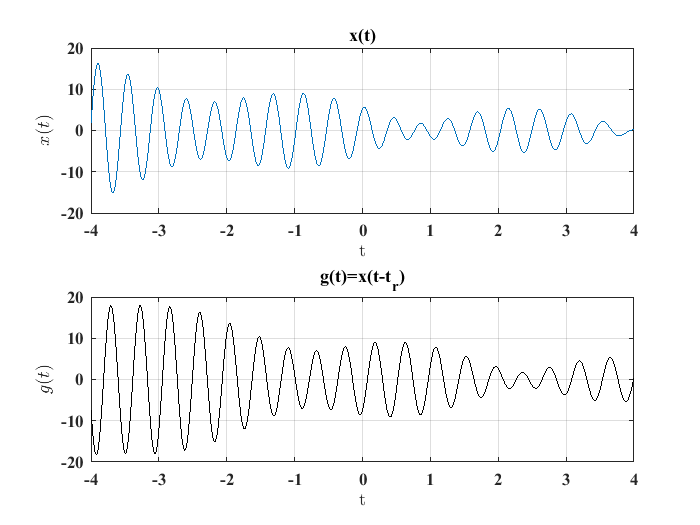
_images/retardo.png — Figura 1 Señal desplazada en el tiempo.#

Operación de escalamiento en el tiempo#

Una versión, escalada en el tiempo de una señal dada $x(t)$ se obtiene si se considera la expresión:

\[ g(t)=x(at) \]

donde $a$ es un número positivo o negativo. Lo anterior se muestra en la siguiente figura:

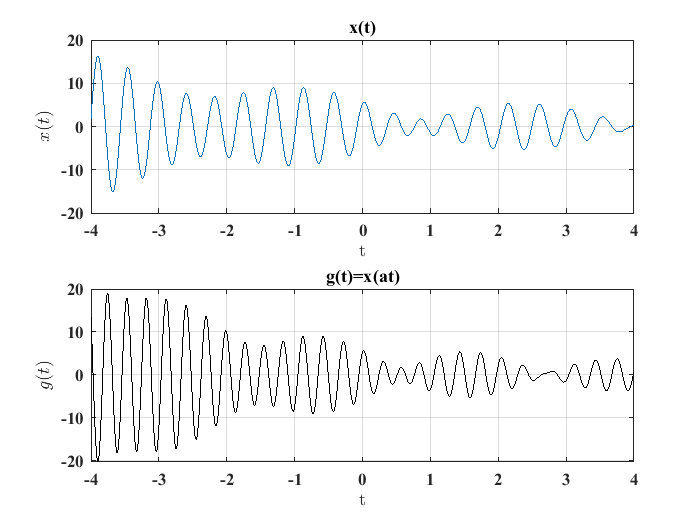
_images/escalada_tiempo.png — Figura 2 Señal escalada en el tiempo.#

Ejercicio 2#

Dada $x(t)=2.5sen(4\pi t)+5.25e^{-0.25t}cos(14.5t)$ obtenga:

\[ g_1(t)=x(t-1.5) \]
\[ g_2(t)=x(1.5t) \]

Operación inversión en el tiempo#

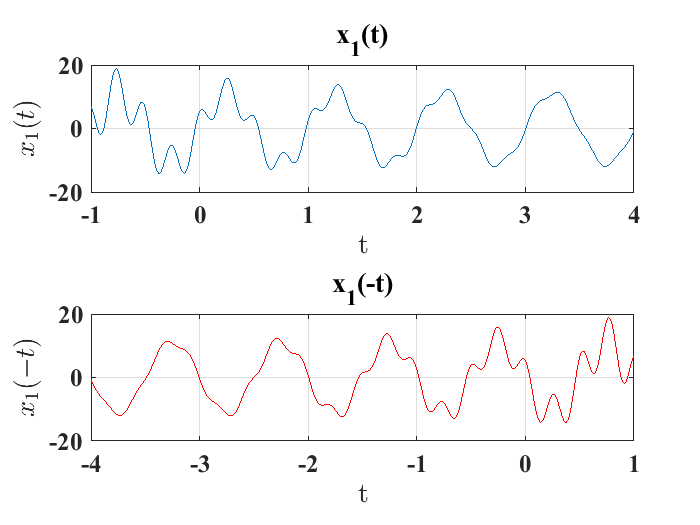
Se obtiene una versión con la característica de inversión en el tiempo mediante la siguiente expresión:

\[ y(t)=x(-t) \]

como se ilustra en la siguiente figura:

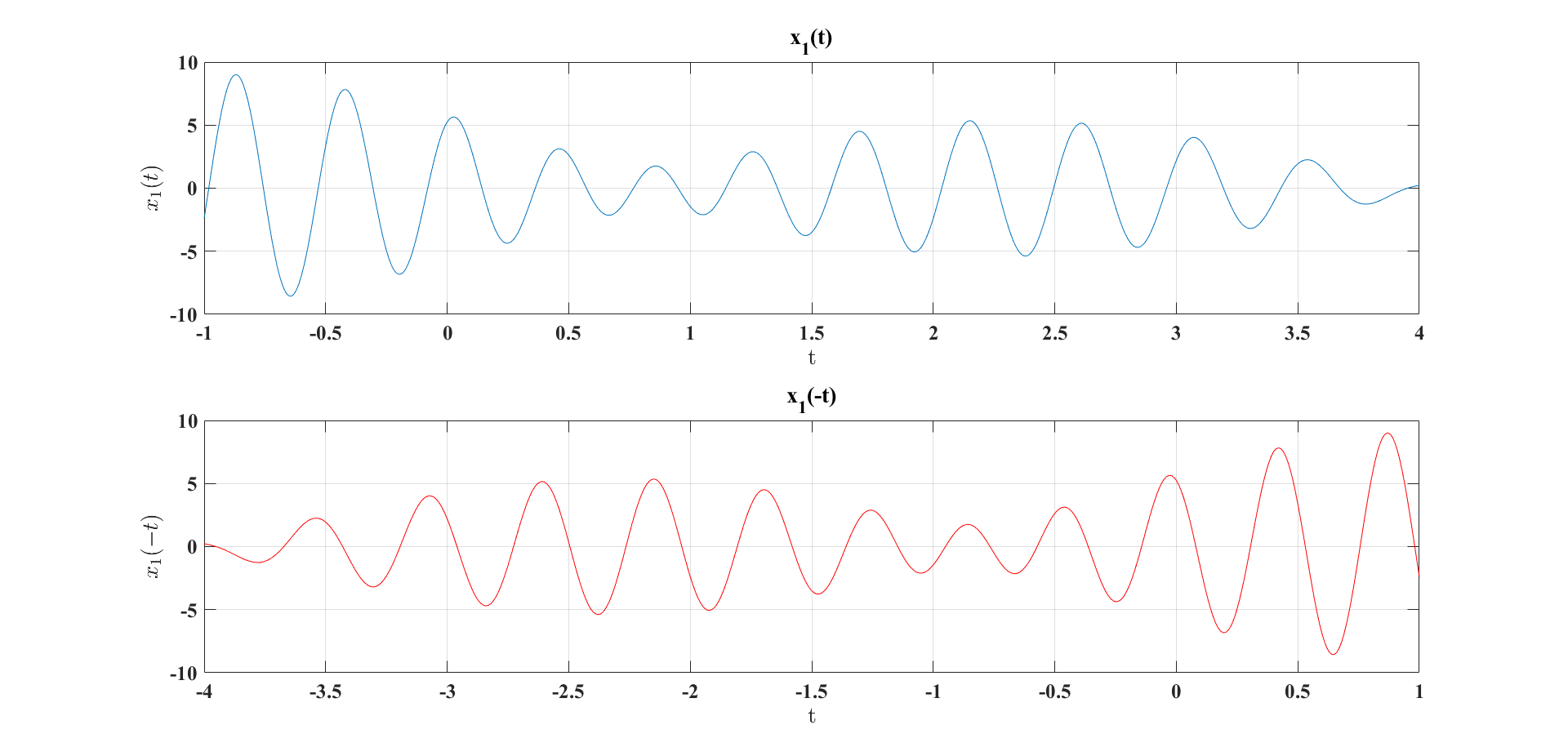
_images/tiempo_invertida.png — Figura 3 Operación de inversión en el tiempo.#

Esta operación en particular se aplica en operaciones más complejas como la convolución que se expone más adelante en el curso. Las siguientes líneas de código generan la versión invertida en el tiempo de la función

\[ x_1(t)=11.25sen(2\pi t)+5.25e^{-0.5t}cos(24.5t) \]

clear
close all
clc

t = [-1:0.01:4];
x1 = @(t) 11.25*sin(2*pi*t)+5.25*exp(-0.5*t).*cos(24.5*t);

subplot(2,1,1)
plot(t,x1(t))
grid
title("x_1(t)")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 


subplot(2,1,2)
plot(-t,x1(t),"r-")
grid
title("x_1(-t)")

 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1(-t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',15);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

_images/295eb5599da868e94c601bc04e937a2ae8457d79d4fa6840fa0d707f26a2c1e7.png

Operaciones derivada e integral#

Las señales también son compatibles con los operadores lineales derivada e integral. por ejemplo para la señal definida como:

(5)#\[\begin{split}\begin{equation} x(t)= \left\{ \begin{array}{lcc} t^2 & si & 0 \leq t \leq 1 \\ \\ -(t^2) & si & 1 < t \leq 2 \end{array} \right. \end{equation}\end{split}\]

con $x(t)=x(t+2)$

El hecho de que se cumpla que $x(t)=x(t+2)$ significa que la función es periódica, es decir se repite cada 2 segundos. Una función $x_p(t)$ es periódica si se cumple que $x_p(t)=x_p(t+T)$, con $T$ un número positivo denominado periodo. Por ejemplo, se cumple que $sen(t)=sen(t+2\pi)$, dado que el periodo del la función seno es $T=2\pi$.

Considere la señal periódica $x_p$ definida por la ecuación (5), gráficamente la señal toma la forma:

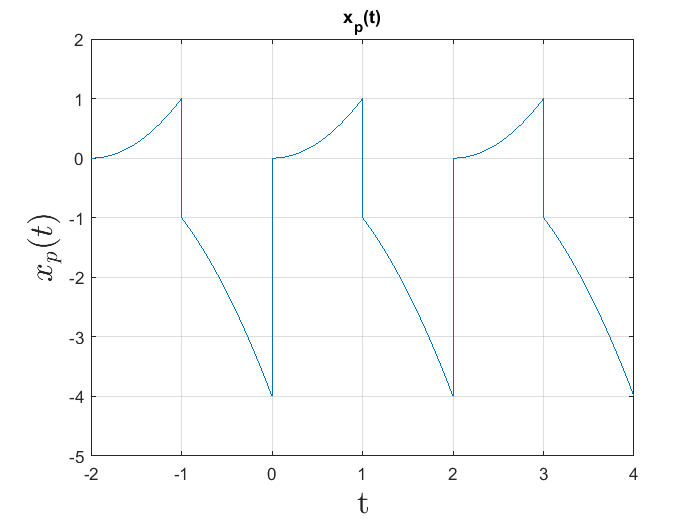
_images/bcdd4906d9629d7164d68c1cb9efa6b472be424b40b044b25c1ccc655703cd59.png

Las operaciones derivada e integral se pueden aplicar a la señal $x(t)$, para obtener las funciones:

\[\begin{split} \begin{eqnarray} g_d(t)=\frac{dx}{dt}\\ g_i(t)=\int xdt \end{eqnarray} \end{split}\]

las cuales se definen como:

(6)#\[\begin{split}\begin{equation} g_d(t)= \left\{ \begin{array}{lcc} 2t & si & 0 \leq t \leq 1 \\ \\ -2t & si & 1 < t \leq 2 \end{array} \right. \end{equation}\end{split}\]

(7)#\[\begin{split}\begin{equation} g_i(t)= \left\{ \begin{array}{lcc} \frac{t^3}{3} & si & 0 \leq t \leq 1 \\ \\ -\frac{t^3}{3} & si & 1 < t \leq 2 \end{array} \right. \end{equation}\end{split}\]

Las gráficas de las funciones $g_d$ y $g_i$ se muestran a continuación:

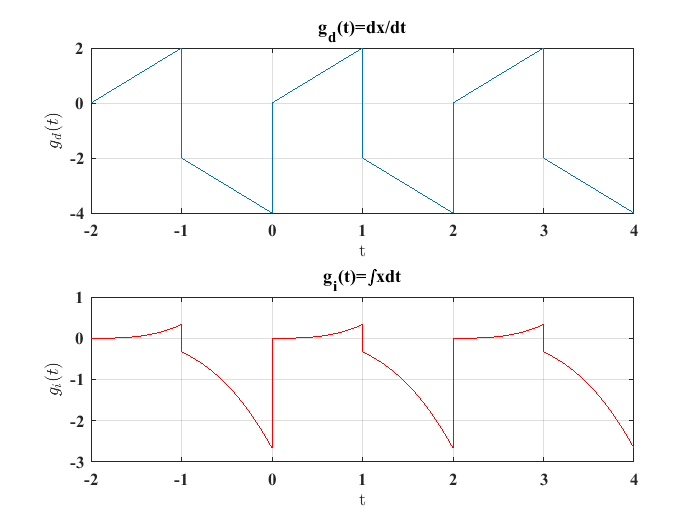
_images/9fdad1c868abeeb51891a1e43f4cc70e0d45665b389b52083d31bf96f2403b7e.png

El código para generar las gráficas anteriores se muestra abajo:

Show code cell source Hide code cell source

clear
close all
clc
t = [0:0.001:2];
x1 = @(t) t.^2.*((0<=t)&(t<=1))-(t.^2).*((1<=t)&(t<=2));
gd = @(t) 2*t.*((0<=t)&(t<=1))-(2*t).*((1<=t)&(t<=2));
gi = @(t) ((t.^3)/3).*((0<=t)&(t<=1))-((t.^3)/3).*((1<=t)&(t<=2));

xp=[x1(t) x1(t) x1(t)];
g_d=[gd(t) gd(t) gd(t)];
g_i=[gi(t) gi(t) gi(t)];

tp=[[-2:0.001:0] [0:0.001:2] [2:0.001:4]];

figure
plot(tp,xp)
axis([-2 4 -5 2])
grid
title("x_p(t)")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_p(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

figure
subplot(2,1,1)
plot(tp,g_d)
grid
title("g_d(t)=dx/dt")
 set(gca,'defaulttextinterpreter','latex')

   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g_d(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)


set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

subplot(2,1,2)
plot(tp,g_i,"r-")

grid
title("g_i(t)=\intxdt")

 set(gca,'defaulttextinterpreter','latex')

   set(get(gca,'XLabel'),'String','t',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g_i(t)$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)


set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

Ejercicio 3#

Aplique la operación integral y derivada a las funciones definidas en las ecuaciones (3) y (4).