La serie trigonométrica de Fourier.

Sea \(x(t)\) una señal periódica, es decir que se puede expresar como \(x(t)=x(t+T)\), donde \(T\) es el periódo de dicha señal en segundos. Según lo descubierto por Joseph Fourier (Kamen and Heck [KH07]), una señal periódica se puede representar como la sumatoria de una infinidad de términos seno y coseno, usando la siguiente expresión:

(96)\[\begin{equation} x(t)=a_0+\sum^{\infty}_{k=1}\left[a_kcos(k\omega_0t)+b_ksen(k\omega_0t)\right],~~-\infty<t<\infty \end{equation}\]

donde \(\omega_0=\frac{2\pi}{T}\) y los términos \(a_0\), \(a_k\) y \(b_k\) se calculan como

(97)\[\begin{equation} a_0=\frac{1}{T}\int^{T}_{0}x(t)dt \end{equation}\]

(98)\[\begin{equation} a_k=\frac{2}{T}\int^{T}_{0}x(t)cos(k\omega_0t)dt \end{equation}\]

(99)\[\begin{equation} b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt \end{equation}\]

Ejemplo 1, señal diente de sierra.

Considere la señal tipo diente de sierra, definida por la expresión:

(100)\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} 150(t+0.02) & si & -0.02 \leq t \leq -0.01 \\ \\ 150t & si & -0.01 \leq t \leq 0.01 \\ \\ 150(t-0.02) & si & 0.01 < t \leq 0.03 \end{array} \right. \end{equation}\end{split}\]

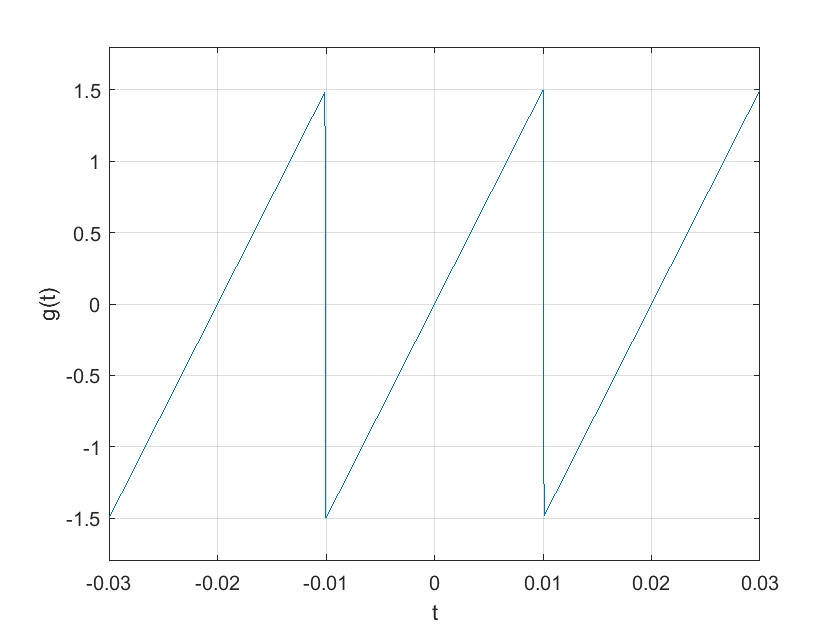
Además, se cumple que \(g(t)=g(t+0.02)\). La gráfica de esta señal, definida por la (100) se muestra con las líneas de código siguientes:

clear
close all
clc

t=[-0.03:0.0001:0.03];
g=(150*(t+0.02)).*((t>=-0.03)&(t<-0.01))+(150*t).*((t>-0.01)&(t<=0.01))+...
   +(150*(t-0.02)).*((t>0.01)&(t<=0.03));

plot(t,g);
xlabel("t");
ylabel("g(t)")
axis([-0.03 0.03 -1.8 1.8]) %La istrucción axis ajusta los ejes de la gráfica
grid;

Los coeficientes \(a_0\), \(a_k\) y \(b_k\) para la serie trigonométrica de Fourier de la señal diente de sierra, definida por la ecuacion (100) se calculan usando las ecuaciones (97), (98) y (99). Dado que \(T=0.02\) y \(\omega_0=100\pi\):

\[\begin{equation}\nonumber a_0=\frac{1}{T}\int^{T}_{0}x(t)dt=\frac{1}{T}\int^{\frac{T}{2}}_{-\frac{T}{2}}x(t)dt=\frac{1}{0.02}\int^{-0.01}_{0.01}150tdt=7500\left[{\frac{t^2}{2}}_{t=-0.01}^{t=0.01}\right]=0 \label{a0sierra} \end{equation}\]

\[\begin{equation}\nonumber a_k=15000\left[{\frac{tsen(100k\pi t)}{100k\pi}}_{t=-0.01}^{t=0.01}-\int^{0.01}_{-0.01}\frac{sen(100k\pi t)}{100k\pi}dt\right] \end{equation}\]

dado que se cumple que \(sen(-x)=-sen(x)\) y \(cos(-x)=cos(x)\):

\[\begin{equation}\nonumber a_k=15000\left[\frac{cos(100k\pi(0.01))}{\left(100k\pi\right)^2}-\frac{cos(100k\pi(-0.01))}{\left(100k\pi\right)^2}\right]=0 \end{equation}\]

Para los coeficientes \(b_k\) se expresa:

\[\begin{equation}\nonumber b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt=\frac{2}{0.02}\int^{0.01}_{-0.01}150tsen(k\omega_0t)dt \end{equation}\]

\[\begin{equation}\nonumber b_k=-\frac{3}{k\pi}\left[cos(k\pi)\right],k=1,2,3... \end{equation}\]

El código de MATLAB que permite calcular la serie trigonométrica de Fourier de la función diente de sierra, considerando los primeros 15 términos de la serie, es decir, con \(n=15\) es el siguiente

n = 100;   
figure
hold on 

x_t =0*t;

for k = 1:n
     bn = -3/(k*pi)*(cos(k*pi));
     x_t = x_t + bn*sin(100*k*pi*t);
end

plot(t,x_t,'k'),grid

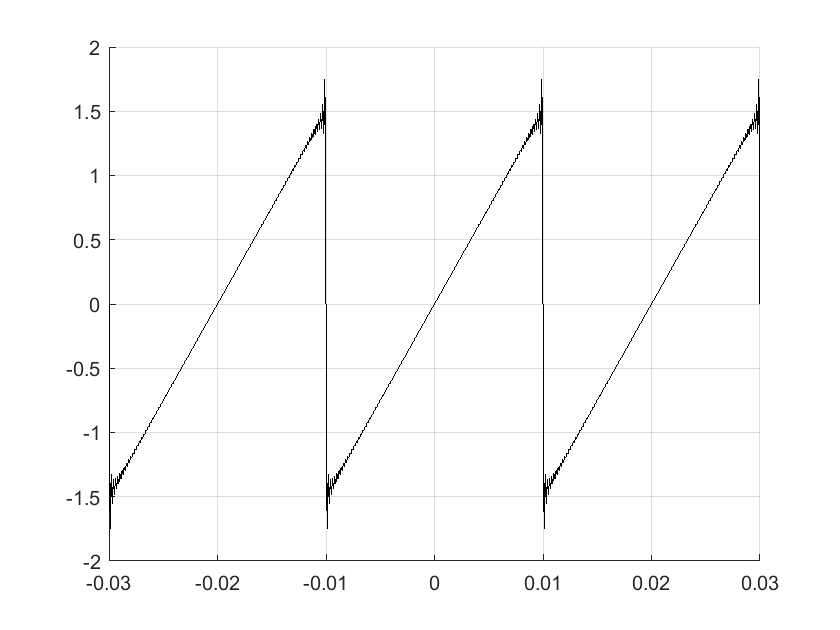
Para comparar \(g(t)\) con su aproximación usando la serie trigonométrica de Fourier se usan las instrucciones siguientes:

figure
plot(t,g);
xlabel("t");
ylabel("g(t)")
axis([-0.03 0.03 -1.8 1.8]) %La istrucción axis ajusta los ejes de la gráfica
grid;
hold on
plot(t,x_t,'k')
legend("Señal diente de sierra","Aproximación con 15 términos")

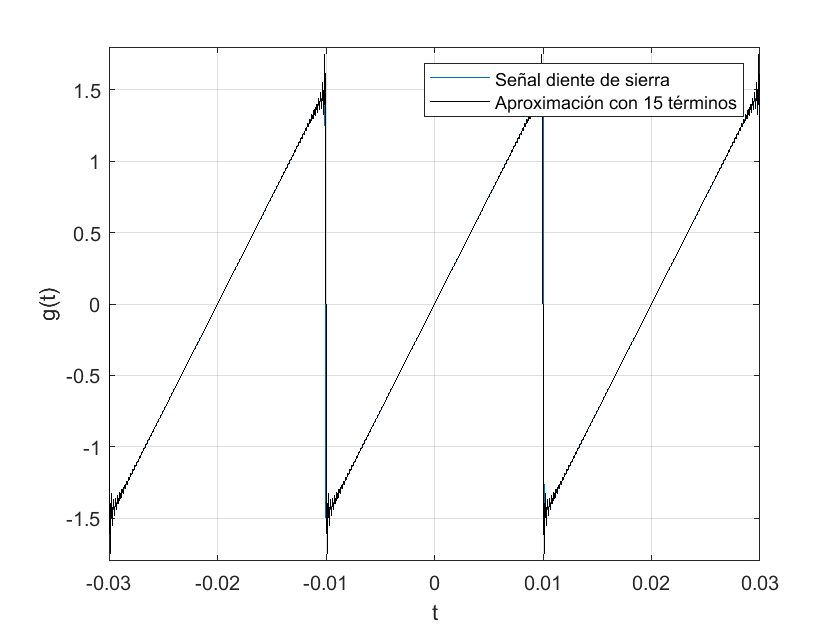
Entre más términos se consideren de la aproximación, es decir, entre mayor sea n en el programa, más parecida será la aproximación, por ejemplo, con \(n=100\):

n = 100;   
figure
hold on 

x_t =0*t;

for k = 1:n
     bk = -3/(k*pi)*(cos(k*pi));
     x_t = x_t + bk*sin(100*k*pi*t);
end

plot(t,x_t,'k')

grid

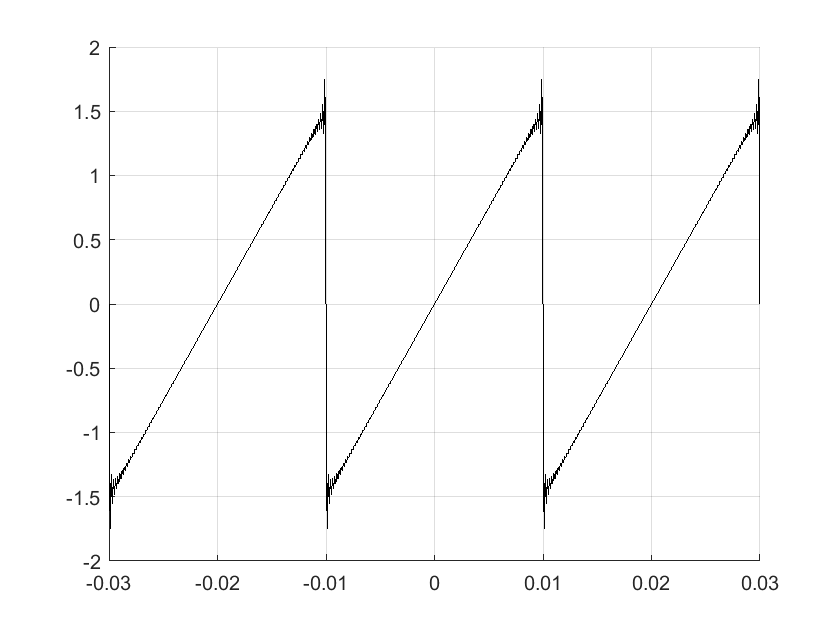
A la distorción en las discontinuidades o cambios en la señal se le conoce como fenómeno de Gibbs Kamen and Heck [KH07].

Ejemplo 2, pulso cuadrado.

Cosidere una función tipo pulso cuadrado, definida por la ecuación:

(101)\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} 5 & si & -0.5 \leq t \leq 0.5 \\ \\ 0 & si & 0.5 \leq t \leq 1.5 \end{array} \right. \end{equation}\end{split}\]

clear
close all
clc

t=[-2:0.0001:2];
s=1*((t>=-2)&(t<=-1.5))+1*((t>-0.5)&(t<=0.5))+1*((t>1.5)&(t<=2));

plot(t,s,"linewidth",2);
xlabel("t");
ylabel("s(t)")
axis([-2 2 0 1.2]) %La istrucción axis ajusta los ejes de la gráfica
grid;

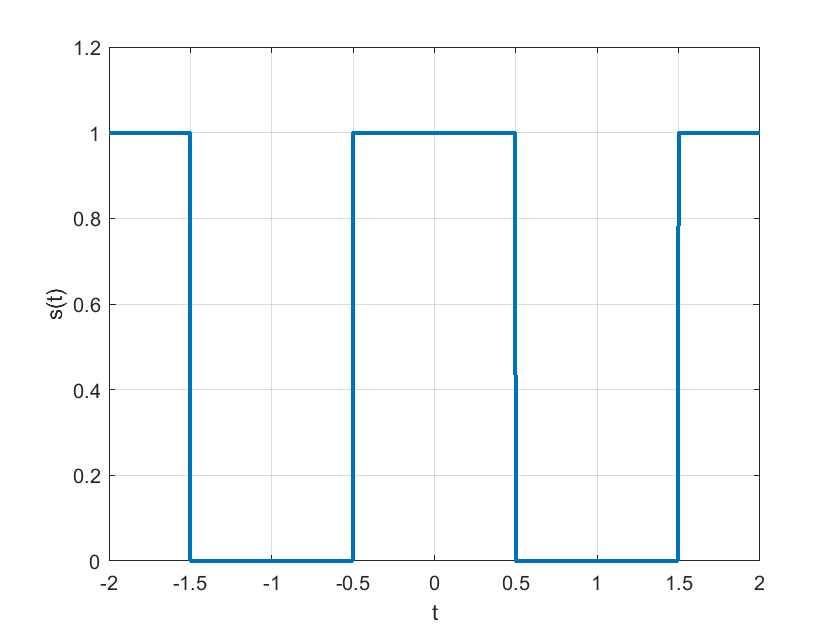
La aproximación por medio de la serie trigonométrica de Fourier se obtiene usando las ecuaciones (97) a (99) y considerando que \(\omega_0=\frac{2\pi}{T}=\frac{2\pi}{2}=\pi\)

\[ \begin{equation}\nonumber a_0=\frac{1}{T}\int^{T}_{0}x(t)dt=\frac{1}{2}\int^{2}_{0}x(t)dt=\frac{1}{2}\int^{0.5}_{0}(1)dt+\frac{1}{2}\int^{2}_{1.5}(0)dt+\frac{1}{2}\int^{2}_{1.5}(1)dt=\frac{1}{2} \end{equation} \]

\[ \begin{equation}\nonumber a_k=\frac{2}{T}\int^{T}_{0}x(t)cos(k\omega_0t)dt=\frac{2}{2}\int^{2}_{0}x(t)cos(k\omega_0t)dt=\int^{0.5}_{0}cos(k\omega_0t)dt+\int^{2}_{1.5}cos(k\omega_0t)dt \end{equation} \]

\[ \begin{equation}\nonumber a_k=\int^{0.5}_{0}cos(k\omega_0t)dt+\int^{2}_{1.5}cos(k\omega_0t)dt={\frac{1}{\pi k}sen(k\pi t)}_{t=0}^{t=0.5}+{\frac{1}{\pi k}sen(k\pi t)}_{t=1.5}^{t=2} \end{equation} \]

\[ \begin{equation}\nonumber a_k=\frac{1}{k\pi}\left[sen\left(\frac{k\pi}{2}\right)-sen\left(\frac{3k\pi}{2}\right)\right]=\frac{2}{k\pi}sen\left(\frac{k\pi}{2}\right),k=1,2,3... \end{equation} \]

Para los coeficientes \(b_k\) se expresa:

\[ \begin{equation}\nonumber b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt=\frac{2}{2}\int^{2}_{0}x(t)sen(k\omega_0t)dt=\int^{0.5}_{0}sen(k\omega_0t)dt+\int^{1}_{1.5}sen(k\omega_0t)dt \end{equation} \]

\[ \begin{equation}\nonumber b_k=\int^{0.5}_{0}sen(k\omega_0t)dt+\int^{1}_{1.5}sen(k\omega_0t)dt={\frac{-1}{\pi k}cos(k\pi t)}_{t=0}^{t=0.5}+{\frac{-1}{\pi k}cos(k\pi t)}_{t=1.5}^{t=2} \end{equation} \]

\[ \begin{equation}\nonumber b_k=\frac{-1}{k\pi}\left[-1+1\right]=0,~~~k=1,2,3... \end{equation} \]

La aproximación por medio de la serie trigonométrica de Fourier se obtiene usando las ecuaciones (97) a (99) y considerando que \(\omega_0=\frac{2\pi}{T}=\frac{2\pi}{0.2}=10\pi\), como se muestra en la figura generada en MATLAB como sigue:

n = 100;   
figure
hold on 

x_t =0*t+0.5;

for k = 1:n
     ak = 2/(k*pi)*sin(k*pi/2);
     x_t = x_t +ak*cos(k*pi*t);
end

plot(t,x_t,'k'),grid

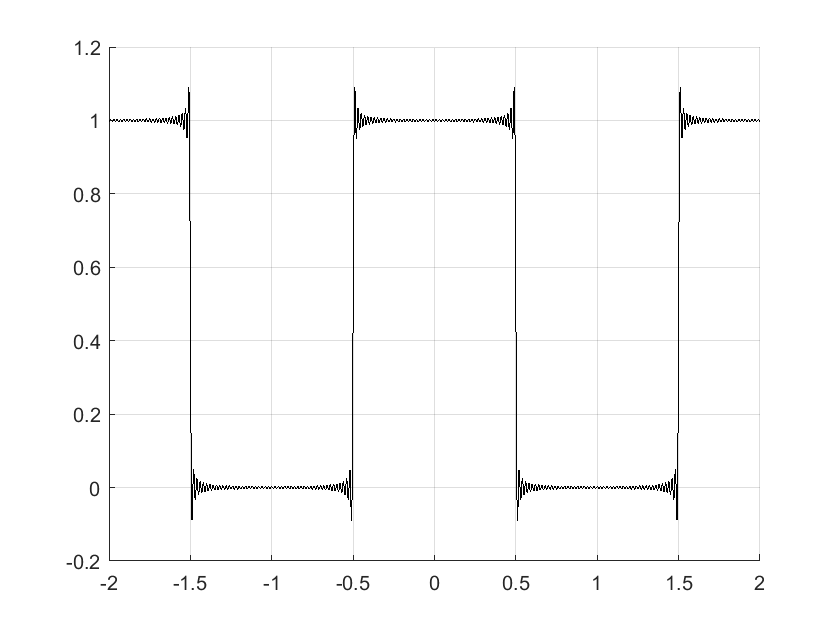
Ejemplo 3, señal modulada por ancho de pulso.

Considere ahora una señal modulada por ancho de pulso definida por la expresión:

(102)\[\begin{split}\begin{equation} g(t)= \left\{ \begin{array}{lcc} 5 & si & -1.5 \leq t \leq 0.5 \\ \\ 0 & si & 0.2 \leq t \leq 0.25 \end{array} \right. \end{equation}\end{split}\]

\(g(t)=g(t+0.2)\)

La aproximación por medio de la serie trigonométrica de Fourier se obtiene usando las ecuaciones (97) a (99) y considerando que \(\omega_0=\frac{2\pi}{T}=\frac{2\pi}{0.2}=10\pi\), como se muestra en la figura generada en MATLAB como sigue:

clear
close all
clc

t=[-0.03:0.0001:0.6];
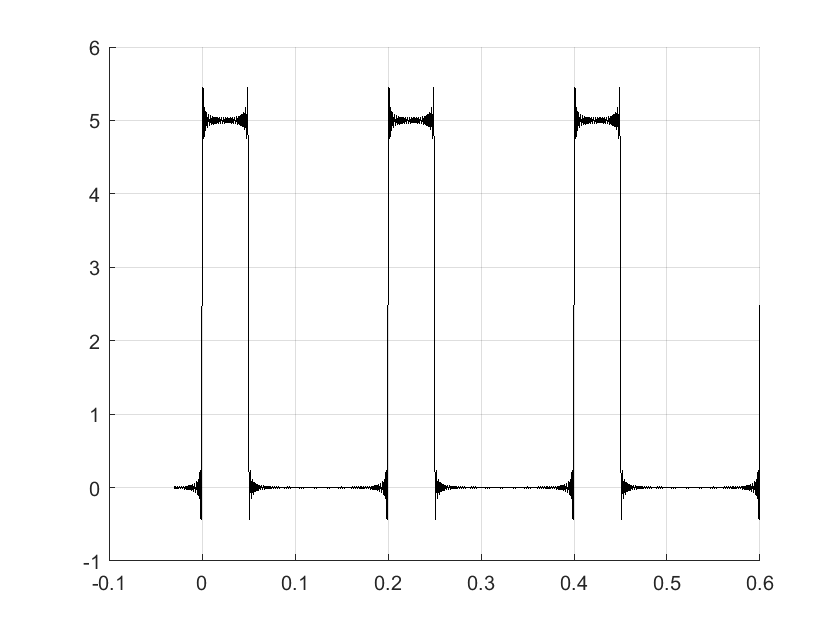
s=5*((t>=0)&(t<=0.05))+5*((t>0.2)&(t<=0.25))+5*((t>0.4)&(t<=0.45));

plot(t,s,"linewidth",2);
xlabel("t");
ylabel("s(t)")
axis([0 0.6 0 5.5]) %La istrucción axis ajusta los ejes de la gráfica
grid;

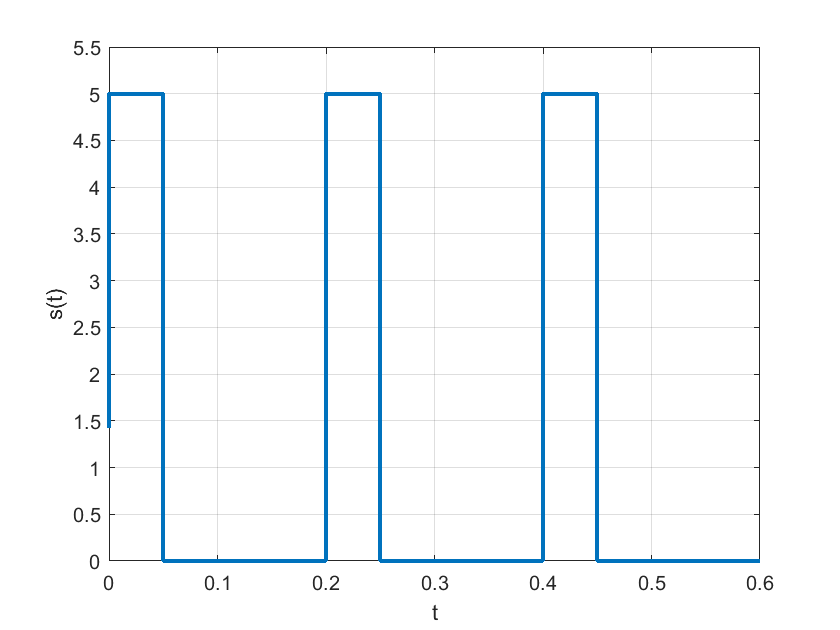
Los coficientes de la serie trigonométrica de fourier para la aproximación de la señal \(s(t)\) se calculan usando las ecuaciones (97), (98) y (99) para obtener:

\[ \begin{equation} a_0=\frac{1}{T}\int^{T}_{0}x(t)dt=\frac{1}{0.2}\int^{0.2}_{0}x(t)dt=5\int^{0.05}_{0}5dt=25 \left [ t_{t=0}^{t=0.05}\right ]=1.25 \end{equation} \]

\[ \begin{equation} a_k=\frac{2}{T}\int^{T}_{0}x(t)cos(k\omega_0t)dt=\frac{1}{0.2}\int^{0.05}_{0}5cos(k\omega_0t)dt \end{equation} \]

\[ \begin{equation}\nonumber a_k=50 \left [ \frac{sen(10k\pi t)}{10k\pi}_{t=0}^{t=0.05} \right ]=\frac{5}{k\pi}sen\left( \frac{k\pi}{2}t\right ),~~~k=1,2,3... \end{equation} \]

Para los coeficientes \(b_k\) se expresa:

\[ \begin{equation}\nonumber b_k=\frac{2}{T}\int^{T}_{0}x(t)sen(k\omega_0t)dt=\frac{10}{0.2}\int^{0.05}_{0}sen(k\omega_0t)dt \end{equation} \]

\[ \begin{equation}\nonumber b_k=5\left[{\frac{-cos(10k\pi t)}{10k\pi}}_{t=0}^{t=0.05}\right] \end{equation} \]

\[ \begin{equation}\nonumber b_k=\frac{5}{k\pi}\left[1-cos\left ( \frac{k\pi}{2}t \right )\right],k=1,2,3... \end{equation} \]

n = 100;   
figure
hold on 

x_t =0*t+1.25;

for k = 1:n
     ak = 5/(k*pi)*sin(k*pi/2);
     bk = 5/(k*pi)*(1-cos(k*pi/2));
     x_t = x_t +ak*cos(10*k*pi*t)+bk*sin(10*k*pi*t);
end

plot(t,x_t,'k'),grid