Solución al primer examen parcial.#
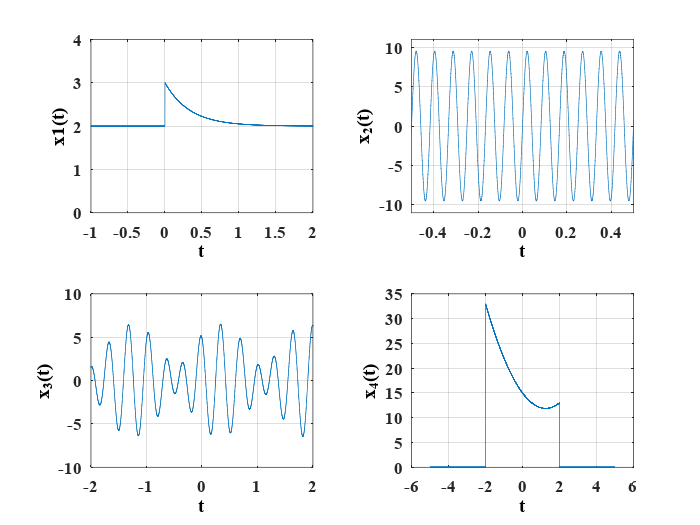
Considere las siguientes señales:
Grafique las siguientes señales, aplicando las operaciones indicadas:
a) \(g_1(t)=x_1x_2+2x_4-3\)
b) \(g_2(t)=(x_1x_2)^2+2.5x_3(2t)+2x_2\left( \frac{t}{3} \right )\)
c) \(g_3(t)=x_1(-3.5t)+2x_4\)
d) \(g_4(t)=0.2x_1^3-0.5x_2^2-7.2x_3\)
Se obtiene usando las líneas de código:
clear
close all
clc
t = [-5:0.001:5];
x1=@(t) exp(-3*t).*(t>=0)+2;
x2=@(t) 9.5*sin(24*pi*t);
x3=@(t) 2.5*cos(15*t+1.2)+4*sin(19*t+1.5);
x4=@(t) (2*t.^2-5*t+15).*((t>-2)&(t<2));
subplot(2,2,1)
plot(t,x1(t))
axis([-1 2 0 4])
grid
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x1(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
subplot(2,2,2)
plot(t,x2(t))
axis([-0.5 0.5 -11 11])
grid
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x_2(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
subplot(2,2,3)
plot(t,x3(t))
axis([-2 2 -10 10])
grid
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x_3(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
subplot(2,2,4)
plot(t,x4(t))
grid
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x_4(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
Operaciones con señales#
A continuación se presentan las opraciones solicitadas:
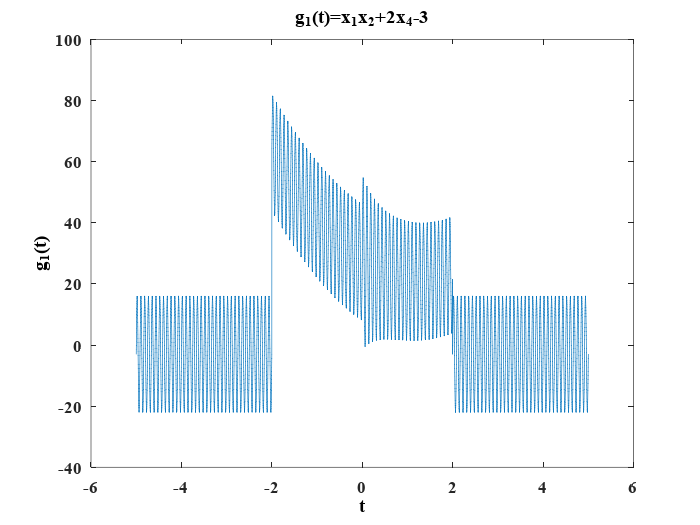
a) \(g_1(t)=x_1x_2+2x_4-3\)
Se obtiene usando las líneas de código:
g1=x1(t).*x2(t)+2*x4(t)-3;
grid
plot(t,g1)
title("g_1(t)=x_1x_2+2x_4-3")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g_1(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
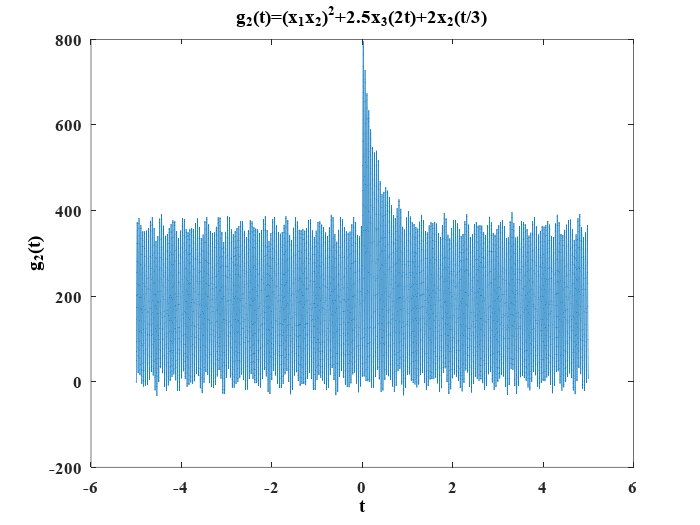
b) \(g_2(t)=(x_1x_2)^2+2.5x_3(2t)+2x_2\left( \frac{t}{3} \right )\)
Se obtiene usando las líneas de código:
g2=(x1(t).*x2(t)).^2+2.5*x3(2*t)+2*x2(t/3);
figure
grid
plot(t,g2)
title("g_2(t)=(x_1x_2)^2+2.5x_3(2t)+2x_2(t/3)")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g_2(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
c) \(g_3(t)=x_1(-3.5t)+2x_4\)
En este caso, es necesario representar a la señal \(x_1(t)\) de manera reflejada respecto del eje \(y\), lo cual se logra con la siguiente representación usando las líneas de código:
%En este caso, es necesario representar a la señal x1 de manera reflejada respecto del eje y
% Lo cual se logra con la siguiente representación:
x_reflejo=exp(3*t).*(t<=0)+2;
figure
plot(t,x_reflejo)
title("x_1(-t)")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x_1(-t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
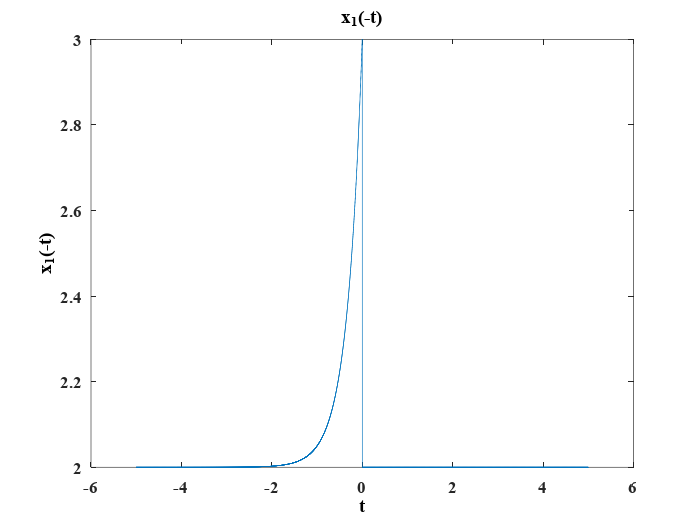
Después, se representa \(x_1(-3.5t)\) con las siguientes líneas de código:
x_reflejo_escalada=exp(3.5*3*t).*(t<=0)+2;
figure
plot(t,x_reflejo_escalada)
title("x_1(-3.5t)")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','x_1(-3.5t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
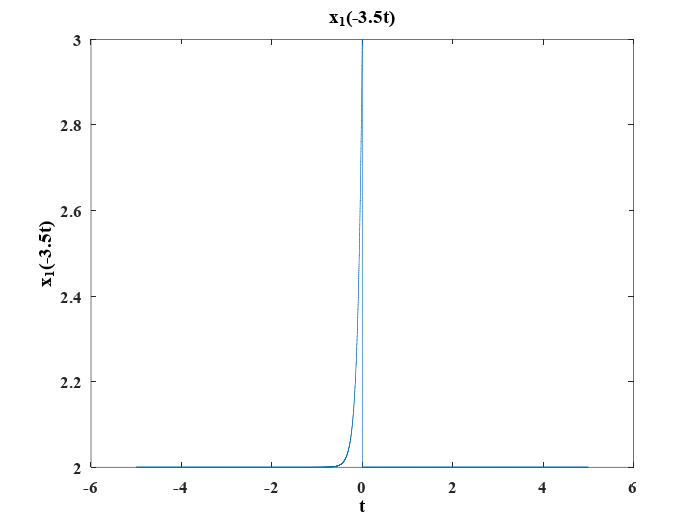
Finalemente, se obtiene \(g_3(t)=x_1(-3.5t)+2x_4\) usando el siguiente código:
x_reflejo_escalada=exp(3.5*3*t).*(t<=0)+2;
figure
plot(t,x_reflejo_escalada+2*x4(t))
title("g_3(t)=x_1(-3.5t)+2x_4(t)")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g_3(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
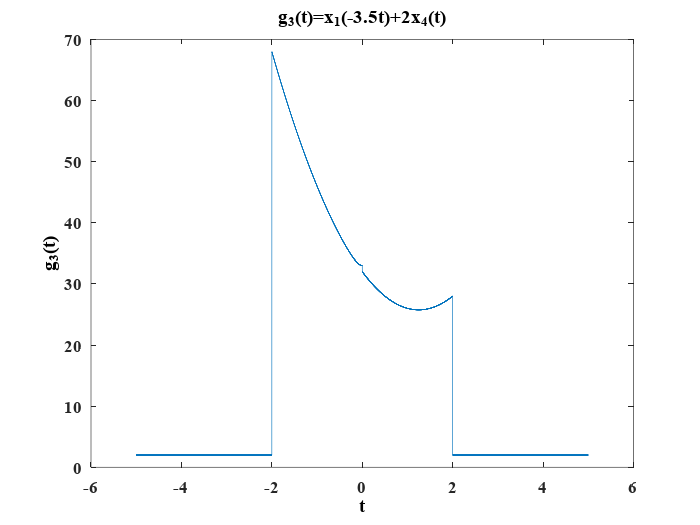
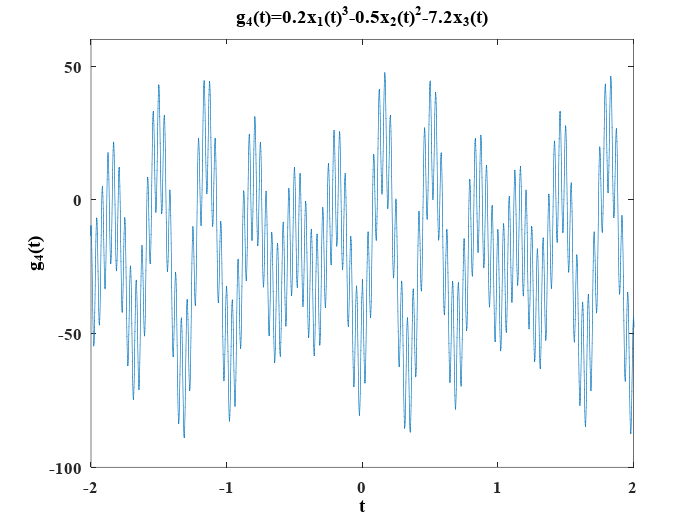
d) g_4(t)=0.2x_1^3-0.5x_2^2-7.2x_3
Se obtiene usando las líneas de código:
g4=0.2*x1(t).^3-0.5*x2(t).^2-7.2*x3(t);
figure
grid
plot(t,g4)
axis([-2 2 -100 60])
title("g_4(t)=0.2x_1(t)^3-0.5x_2(t)^2-7.2x_3(t)")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','t',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g_4(t)',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
Determinar si las siguiente señales son de potencia o de energía y calcular el valor RMS cuando aplique#
a) \(x(t)=4.5cos(4\pi t)+6.75sen(4\pi t)-7.2cos(12\pi t)\)
b) \(y(t)=e^{-\frac{3t}{2}}\) para \(t \ge 0\).
c) La función definida como:
donde \(z(t)=z(t+4)\)
Solución:
a) La función \(x(t)=4.5cos(4\pi t)+6.75sen(4\pi t)-7.2cos(12\pi t)\) está compuesta por tres señales periódicas, que se pueden simplificar usando la identidad trigonométrica siguiente:
Para simplificar la suma: \(4.5cos(4\pi t)+6.75sen(4\pi t)\), se observa que, si se considera \(\omega=4\pi\) se puede expresar:
\(Acos(4\pi t+\theta)=4.5cos(4\pi t)-6.75sen(4\pi t)\)
De donde se desprende que:
\(Acos(\theta)=4.5\) y \(-Asen(\theta)=6.75\)
Resolviendo para \(\theta\):
\(\frac{-Asen(\theta)}{Acos(\theta)}=-tan(\theta)=\frac{6.75}{4.5}=1.5\)
finalmente \(\theta=-tan^-1(1.5)=-0.9827~rad\)
El valor de la constante \(A\) se obtiene como:
\(-Asen(\theta)=6.75\), resolviendo para \(A\):
\(A=\frac{-6.75}{sen(-0.9827)}=8.1129\)
Sustituyendo en la expresión equivalente:
\(x(t)=8.1129cos(4\pi t -0.9827)-7.2cos(12\pi t)\)
De manera que el valor RMS de la señal está dado por:
\(X_{RMS}=\sqrt{\frac{8.1129^2}{2}+\frac{7.2^2}{2}}=7.67\)
en este caso. \(x(t)\) es una señal de potencia.
b) La señal \(y(t)=e^{-\frac{3t}{2}}\) para \(t \ge 0\) es una señal de decaimiento, la cual no es periódica, por lo tanto, es una señal de energía y es el único parámetro que hace sentido calular:
\(E_x=\int_{-\infty}^{\infty}x^{2}dt=\int_{0}^{\infty}(e^{-\frac{3t}{2}})^{2}dt=\int_{0}^{\infty}e^{-3t}dt=-\frac{e^{-3(\infty)}}{3}+\frac{e^{0}}{3}=\frac{1}{3}\)
c) La señal \(z(t)\) una señal cuadrada de ampitud \(A=5.25\) con periodo \(4\), por lo tanto se trata de una señal de potencia, por lo cual hace sentido calcular su valor RMS:
\(Z_{RMS}=\sqrt{\frac{1}{T}\int^{T}_{0} z^2(t) dt}=\sqrt{\frac{1}{4}\int^{4}_{0} z^2(t) dt}=\sqrt{\frac{1}{4}\int^{2}_{0}(5.25)^2dt+\frac{1}{4}\int^{4}_{2} (-5.25)^2dt}\)
\(Z_{RMS}=\sqrt{\frac{1}{4}2(5.25)^2-\frac{1}{4}4(-5.25)^2-\frac{1}{4}2(-5.25)^2}=5.25\)
Versión discreta de una señal#
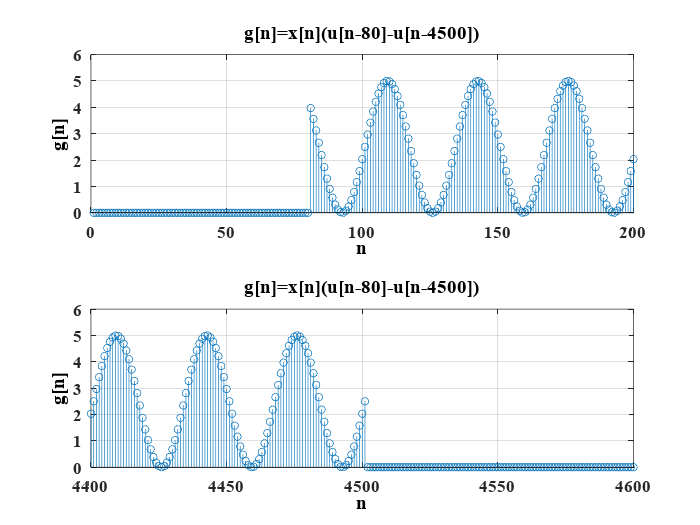
Genere la versión discreta de la señal \(x(t) = 2.5sen(60\pi t)+2.5\), seleccione un periodo de muestreo \(T\) adecuado para generar la gráfica en tiempo discreto de la operación:
donde \(u[n]\) es el escalón unitario.
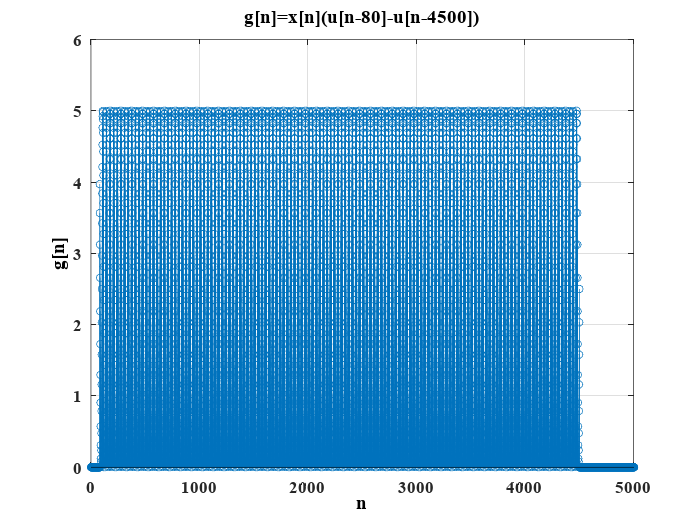
La señal se obtiene en detalle, en los extremos del intervalo con las siguientes líneas de código:
figure
subplot(2,1,1)
stem(gn)
axis([0 200 0 6])
grid
title("g[n]=x[n](u[n-80]-u[n-4500])")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','n',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g[n]',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');
subplot(2,1,2)
stem(gn)
axis([4400 4600 0 6])
grid
title("g[n]=x[n](u[n-80]-u[n-4500])")
set(gca,'defaulttextinterpreter','latex')
set(get(gca,'XLabel'),'String','n',...
'FontName','times news roman',... %Ajustes de rótulos y formato de letra
'FontAngle','normal',...
'FontSize',20)
%
set(get(gca,'YLabel'),'String','g[n]',...
'FontName','times news roman',...
'FontAngle','normal',...
'FontSize',20)
set(gca,'fontsize',20);
set(gca,'fontname','Times New Roman','FontWeight','Bold');