Práctica 2: Comprobación de invarianza en el tiempo con MATLAB

La invarianza en el tiempo es otra propiedad importante de los sistemas dinámicos, acompañada de la linealidad, la invarianza en el tiempo permite a los sistemas tener un comportamiento muy deseable para su aplicación en la ingeniería. Matemáticamente, para un sistema con la estructura \(y(t)=Transf\{x(t)\}\) la invarianza en el tiempo se expresa como:

(21)\[\begin{equation} Transf\{x(t-\tau)\}=y(t-\tau) \end{equation}\]

Esto significa que si la señal que se aplica a un sistema invariante en el tiempo se desplaza en el tiempo por \(\tau\) segundos, el único efecto de este retardo deberá ser un desplazamiento igual en la señal de salida.

Condición de invarianza en el tiempo:

(22)\[\begin{equation} Transf\{x(t)\}=y(t)~~implica~que:~~~Transf\{x(t-\tau)\}=y(t-\tau) \end{equation}\]

En esta práctica se comprueba la propiedad de invarianza en el tiempo para sistemas, en forma de estructura \(Transf\{x(t)\}\) para los sistemas:

\[\begin{split} \begin{eqnarray} &y(t)=2.5x(t)\\ &y(t)=4.5x(t)-3\\ &y(t)=(x(t))^2-5tx(t)+2\\ &y(t)=cos(3x(t))+2x(t)\\ &y(t)=e^{(-4.5x(t))}cos(20(t)) \end{eqnarray} \end{split}\]

Con una función arbitraria de entrada \(x(t)=e^{-0.5t}cos(25t)u(t)\)

clear
close all
% Código para comprobar la invarianza en el tiempo de sistemas
%
t = [0:0.01:10];               % Vector de tiempo
x = @(t) exp(-0.5*t).*cos(25*t).*(t>=0);  % Función para generar el estímulo de entrada
% Definición de las estructuras para los sistemas o transformaciones
Transf_a = @(x) 2.5*x;
Transf_b = @(x) 4.5*x+3;
Transf_c = @(x) x.^2-5*t.*x+2;
Transf_d = @(x) cos(3*x)+2*x;
Transf_e = @(x) exp(-4.5*x).*cos(20*t);
y1 = Transf_a(x(t));
y2 = Transf_a(x(t-2.5));
clf;                          % Limpiar figura 
plot(t,y1,'b-',t,y2,'r--');   % Graficar las funciones
title('Respuesta a las entradas x(t) y x(t-2.5)') 
xlabel('t [s]');
ylabel('Amplitud');
legend('Trans\{x(t)\}','Transf\{x(t-2)\}');

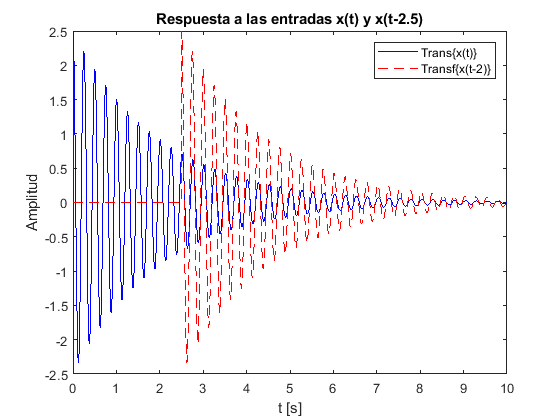
Como es posible observar en la gráfica anterior, el sistema \(y(t-2.5)=2.5x(t-2.5)\) es invariante en el tiempo, dado que cumple con el principio de invarianza. Si el mismo código se ejecuta, pero esta vez evaluando el sistema definido como \(y(t)=x(t)^2-5tx(t)+2\) se obtiene:

clear
close all
% Código para comprobar la invarianza en el tiempo de sistemas
%
t = [0:0.01:10];               % Vector de tiempo
x = @(t) exp(-0.5*t).*cos(25*t).*(t>=0);  % Función para generar el estímulo de entrada
% Definición de las estructuras para los sistemas o transformaciones
Transf_a = @(x) 2.5*x;
Transf_b = @(x) 4.5*x+3;
Transf_c = @(x) x.^2-5*t.*x+2;
Transf_d = @(x) cos(3*x)+2*x;
Transf_e = @(x) exp(-4.5*x).*cos(20*t);

y1 = Transf_c(x(t));
y2 = Transf_c(x(t-2.5));
clf;                          % Limpiar figura 
plot(t,y1,'b-',t,y2,'r--');   % Graficar las funciones
title('Respuesta a las entradas x(t) y x(t-2.5)') 
xlabel('t [s]');
ylabel('Amplitud');
legend('Trans\{x(t)\}','Transf\{x(t-2)\}');

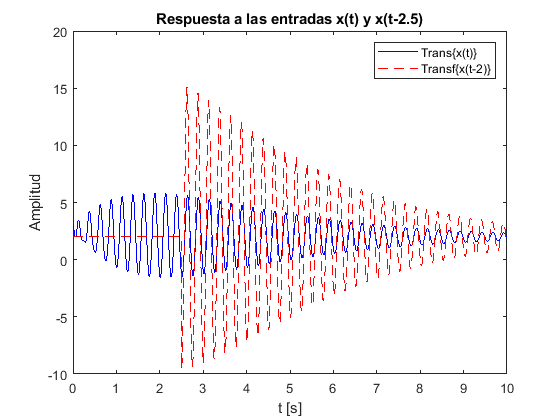
En este caso el sistema es variante en el tiempo, dado que las gráficas de \(Transf\{x(t-\tau)\}\) y \(y(t-\tau)\) son diferentes.