Respuesta al impulso de sistemas de tiempo continuo.

Una ecuación diferencial ordinaria, lineal y de coeficientes constantes se puede utilizar como el modelo matemático o la respresentación de un sistema dinámico. Existe una representación alternativa que resulta muy útil para el modelado de los sistemas es llamada la respuesta al impulso del sistema(Kamen and Heck [KH07], Alkin [Alk14]). La función impulso unitario, conocida como función Delta de Dirac se define matemáticamente como:

(44)\[\begin{split}\begin{equation} \delta(t)= \left\{ \begin{array}{lcc} 1 & si & 0 = t \\ \\ 0 & si & t \neq 0 \end{array} \right. \end{equation}\end{split}\]

Cuando la función \(\delta(t)\) se usa como una función estímulo para un sistema, a la salida \(y(t)\) se le denomina respuesta al impulso del sistema y se usa la notación \(h(t)\) para distinguirla de las posibles salidas del sistema ante entradas o estímulos arbitrarios \(x(t)\).

Determinación de la respuesta al impulso de un sistema

Como hemos observado en la Práctica 3, es posible determinar la salida \(y(t)\) de un sistema, al resolver la ecuación diferencial que modela al sistema. Esta ecuación puede ser homogénea o forzada, con las soluciones candidatas condensadas en Tabla 1 y Tabla 3. Entre las funciones candidatas mostradas en tales tablas, no se presenta en ningún caso la función impulso unitario definida en la ecuación (44), sin embargo se cumple que:

(45)\[\begin{equation} \frac{du(t)}{dt}=\delta(t) \end{equation}\]

Determinación de la respuesta al impulso de un sistema:

Para poder encontrar la respuesta forzada de un sistema cuando el estímulo o entrada es una señal del tipo impulso unitario se procede a encontrar la respuesta al escalón unitario del sistema (caso cuando la entrada es una constante de amlitud 1) y se obtiene la derivada de la respuesta resultante.

Sea \(y(t)\) la respuesta al escalón unitario \(u(t)\) de un sistema, es decir \(y(t)=Transf\{u(t)\}\), la respuesta al impulso unitario \(h(t)=Transf\{\delta(t)\}\) de ese sistema es:

(46)\[\begin{equation} \frac{dy(t)}{dt}=h(t) \end{equation}\]

Por ejemplo para el sistema eléctrico analizado en el caso anterior, cuyo diagrama se muestra en la Figura 7 y cuyos parámetros son los de la Tabla 4, la respuesta al impulso de obtiene encontrando primero su respuesta al escalón unitario, es decir, cuando el modelo del sistema es:

(47)\[\begin{equation} 1.661\times 10^{-5}\frac{d^2v_c(t)}{dt^2}+ 0.0018\frac{dv_c(t)}{dt}+v_c(t)=u(t) \end{equation}\]

Se consideran condiciones iniciales cero, es decir: \(v(0)=0\) y \(\dot{v}(0)=0\) y además \(u(t)=1\) para \(t>0\) para obtener:

(48)\[\begin{equation} 1.661\times 10^{-5}\frac{d^2v_c(t)}{dt^2}+ 0.0018\frac{dv_c(t)}{dt}+v_c(t)=1 \end{equation}\]

De aquí se desprende que, de acuerdo con la Tabla 1 y de acuerdo con el ejemplo anterior, donde se calcularon las raices complejas \(-52.98 \pm 239.58i\) la solución de la homogenea asociada es:

\[ v_{ch}=(C_1cos(239.58t)+C_2sen(239.58t))e^{-52.98t} \]

Para este sistema, se cumple que la solución particular es una constante, \(v_{cp}=1\), por lo tanto la solución completa para el voltaje en el capacitor adquiere la forma:

(49)\[\begin{equation} v_c(t)=v_{ch}+v_{p}=(C_1cos(239.58t)+C_2sen(239.58t))e^{-52.98t}+1 \end{equation}\]

Sabiendo que \(v_c(0)=0\) y \(\dot{v}_c(0)=0\) y sustituyendo la ecuación (49) en la ecuación (47) se obiene el valor de los coeficientes \(C_1\) y \(C_2\).

\[\begin{split} \begin{eqnarray} v_c(t)=(C_1cos(239.58t)+C_2sen(239.58t))e^{-52.98t}+1\\ \dot{v}_c(t)=\frac{d[(C_1cos(239.58t)+C_2sen(239.58t))e^{-52.98t}+1]}{dt}\\ \end{eqnarray} \end{split}\]

Evaluando \(v_c(0)\) y \(\dot{v}_c(0)\):

(50)\[\begin{split}\begin{eqnarray} v_c(0)=(C_1cos(239.58(0))+C_2sen(239.58(0)))e^{-52.98(0)}+1=0\\ \dot{v}_c(0)=(-239.58C_1sen(0)+239.58C_2cos(0))e^{0}-52.98(C_1cos(0)+C_2sen(0))e^{0} \end{eqnarray}\end{split}\]

Las ecuaciones (50) conducen a:

\[ v_c(0)=(C_1cos(0)+C_2sen(0))e^{0}+1=0\Longrightarrow C_1=-1 \]

Sustituyendo \(C_1\) en la ecuación (40)

\[ \dot{v}_c(0)=(390.5154sen(0)+239.58C_2cos(0))e^{0}-52.98(-cos(0)+C_2sen(0))e^{0}=0 \]

De donde se obtiene que:

\[ 239.58C_2+52.98=0\Longrightarrow C_2=-0.2211 \]

Luego entonces, la solución completa de la ecuación diferencial, o bien el voltaje en el capacitor \(v_c(t)\) es:

(51)\[\begin{equation} v_c(t)=v_{ch}+v_{cp}=(-cos(239.58t)-0.2211sen(239.58t))e^{-52.98t}+1 \end{equation}\]

La respuesta al impulso es la derivada de \(v_c(t)\) respecto del tiempo, entonces:

(52)\[\begin{equation} h(t)=\frac{v_c(t)}{dt}=\frac{(-cos(239.58t)-0.2211sen(239.58t))e^{-52.98t}+1}{dt} \end{equation}\]

Luego entonces:

(53)\[\begin{eqnarray} h(t)=(261.7287sen(239.58t))e^{-52.98t} \end{eqnarray}\]

La gráfica de la respuesta al impulso del sistema se puede obtener en MATLAB con las siguientes líneas de código:

clear 
close all
clc


t=[0:0.001:0.3];

ht=(261.7287*sin(239.58*t)).*exp(-52.98*t);

plot(t,ht)
set(gcf,'Visible','on')
title("Respuesta al impulso")
xlabel("t [s]")
ylabel("v_c(t) [V]")
set(gca,'fontsize',20);

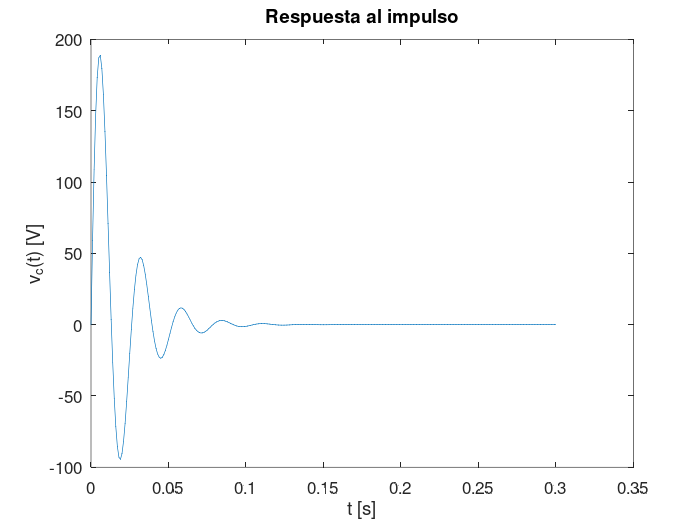
En este caso, tambien se puede obtener una generalización de la respuesta al impulso, ante cambios en alguno de los parámetros del sistema R, L o C dado que la estructura es la misma.

Respuesta al impulso con diferentes parámetros.

Es posible encontrar diferentes respuestas del sistema usando una estructura general para el caso particular cuando la función de estímulo es una constante. Para el caso particular del circuito RLC serie, en el que la respuesta forzada completa obedece la estructura:

(54)\[\begin{equation} v_c(t)=(C_1cos(\beta t)+C_2sen(\beta t))e^{\alpha t}+1 \end{equation}\]

En este caso, dado que se usa un escalón unitario, se determina que \(k=1\). Cuando las condiciones iniciales \(v_c(0)\) y \(\dot{v}_c(0)\) las constantes \(C_1\), \(C_2\) y \(k\) se pueden obtener al encontrar las raices \(r_{i},~i=1,2\) del polinomio auxiliar (38):

\[ r_{i}=\alpha \pm \beta i \]

Usando las partes real e imaginaria de la primera raíz, se encuentra el valor de dichas constantes:

(55)\[\begin{split}\begin{eqnarray} k=1\\ C_1=-1\\ C_2=\frac{-\alpha C_1}{\beta}=\frac{\alpha}{\beta} \end{eqnarray}\end{split}\]

Así, la respuesta al escalón en general es:

(56)\[\begin{equation} v_c(t)=(-cos(\beta t)+\frac{\alpha}{\beta}sen(\beta t))e^{\alpha t}+1 \end{equation}\]

La respuesta al impulso se encuentra al derivar la ecuacion (56) respecto del tiempo:

(57)\[\begin{equation} h(t)=\frac{(-cos(\beta t)+\frac{\alpha}{\beta}sen(\beta t))e^{\alpha t}+1}{dt} \end{equation}\]

Obteniéndose la expresión general:

(58)\[\begin{equation} h(t)=(\beta sen(\beta t)+\alpha cos(\beta t))e^{\alpha t}+\alpha\left(-cos(\beta t)+\frac{\alpha}{\beta}sen(\beta t)\right)e^{\alpha t} \end{equation}\]

(59)\[\begin{equation} h(t)=\left( \beta+\frac{\alpha^2}{\beta} \right)sen(\beta t)e^{\alpha t} \end{equation}\]

El siguiente código en MATLAB permite graficar la respuesta al escalón con diferentes valores de los parámetros RLC para fines comparativos, se genera una respuesta de referencia y después se calculan las raices del nuevo polinomio auxiliar definido en la ecuación (38), para graficar las dos respuestas y compararlas.

clear 
close all


R=1600;
L=15.1; % Parámetros originales o de referencia
C=1.01e-6;

vs=1.63; % Voltaje de la fuente o escalón

t=[0:0.001:0.3]; %Vector de tiempo

raices=roots([L*C R*C 1]); % Cálculo de las raices del polinomio auxiliar

alpha=real(raices(1)); % Se extraen las partes real e imaginaria
betha=imag(raices(1)); 

% Se determinan los valores de C1 y C2 de la solución homogénea
C1=-1;
C2=-alpha*C1/betha;


h_c=(betha+(alpha^2)/betha)*sin(betha*t).*exp(alpha*t);
plot(t,h_c)
xlabel("t [s]")
ylabel("v_c(t) [V]")
hold on % Se deja abierta la imagen para graficar la respuesta con 
% un valor diferente de algún parámetro para fines comparativos

%-------------------------------------------------------------
%  Se calcula la nueva respuesta vc con R=5600
%-------------------------------------------------------------

R=5600; % se acualiza el valor de R

raices=roots([L*C R*C 1]); % Cálculo de las raices del polinomio auxiliar

alpha=real(raices(1)); % Se extraen las partes real e imaginaria
betha=imag(raices(1)); 

% Se determinan los valores de C1 y C2 de la solución homogénea
C1=-1;
C2=-alpha*C1/betha;
k=vs;

h_c2=(betha+(alpha^2)/betha)*sin(betha*t).*exp(alpha*t);
plot(t,h_c2)
legend ('h_c cuando R=1600 \Omega', strcat('h_c cuando R=',num2str(R),' \Omega'));
set(gca,'fontsize',20);
legend ("boxoff");
set(gcf,'Visible','on')