Señales en tiempo discreto.

Como hemos visto en secciones anteriores, la principal diferencia entre las señales analógicas y las señales de tiempo coninuo es que las señales analógicas no están definidas para todo instante de tiempo \(t\), sino que están definidas únicamente en instantes de tiempo específicos, en ingeniería se considera que estos instantes de tiempo están separados por un periodo constante llamado incremento \(T\), mismo que en aplicaciones de adquisición datos se considera como el periodo de muestreo ([Alk14]).

En este orden de ideas, el modelo matemático de las señales de tiempo discreto se define de forma diferente a las señales de tiempo continuo, conceptos como el índice de muestra se utilizan para la descripción del conjunto de valores numéricos que constituyen una señal en tiempo discreto.

Modelo matemático de una señal de tiempo discreto

Dada una señal definida solo en isntantes de tiempo, con un periodo fijo, se dice que es una señal discreta \(x[n]\) y se usa la notación de corchetes para indicar que es un conjunto valores numéricos que describen la evolución en el tiempo de una variable física capturada en esos instantes precisos de tiempo.

\[\begin{split} \begin{eqnarray} \nonumber x[n]&={2.4,1.5,1.23,0.54,3,3.35,4.15}\\ &~~~~~~~~~~\uparrow~~~~~~~~~~~~~~~~~~~~ \end{eqnarray} \end{split}\]

El símbolo \(\uparrow\) indica el elemento \(0\) que corresponde al valor \(n=0\) del índice de muestra, de forma que en este caso se tiene que \(x[-1]=1.5\), \(x[0]=1.23\) y \(x[3]=3.35\).

Las señales en tiempo discretos se representan gráficamente usando gráficas tipo espiga, por ejemplo, la señal:

\[ x[n]=2.5sen[0.24n]+e^{[-0.03n]}cos[4n] \]

Se representa como:

Es importante notar que la función ilustrada anteriormente es determinística, es decir, posee un modelo matemático bien definido y es único, sin embargo la mayoría de las señales discretas vienen de experimentos, por lo tanto se representan por medio de conjuntos de valores numéricos.

Operaciones con señales en tiempo discreto

Las señales, al ser funciones del tiempo, son compatibles con operaciones aritméticas comunes, como lo son la suma, la resta, la multiplicación y la división. Además, existen otras operaciones matemáticas que se puede aplicar a las señales como veremos más adelante como lo son el desplazamiento en el tiempo, el escalamiento en el tiempo y la inversión del vector de tiempo.

Operaciones aritméticas

Adición de una constante

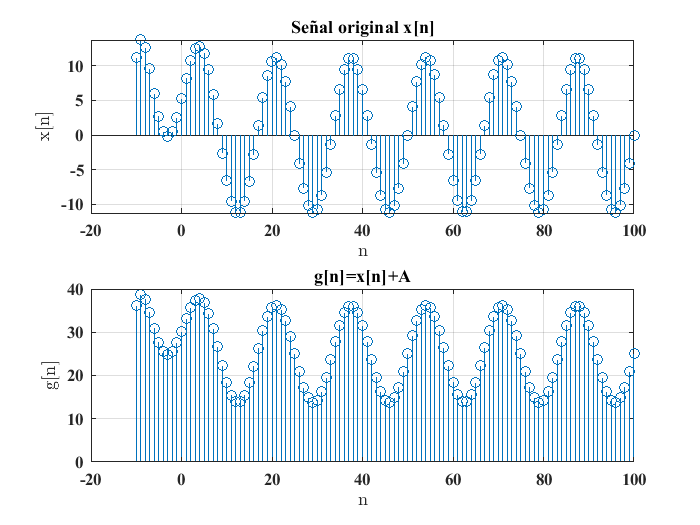
La primera operación a considerar es la adición de una constante \(A\) a una señal, esta constante se conoce como offset. La expresión para esta operación es:

\[ g[n]=x[n]+A \]

donde la señal \(g[n]\) es la que resulta de aplicar la operación de adición de una constante a la señal original. En este caso, a cada uno de los datos de los que se compone la señal \(x[n]\) se le adhiere la constante A.

\[\begin{split} \begin{eqnarray} \nonumber g[-2]=x[-2]+A\\ g[-1]=x[-1]+A\\ g[0]=x[0]+A\\ g[1]=x[1]+A\\ \end{eqnarray} \end{split}\]

Lo anterior se ejemplifica usando el código:

clear
close all
n = [-10:1:100];
x = @(n) 11.25*sin(0.12*pi*n)+5.25*exp(-0.25*n).*cos(0.15*n);

A=25;
g_n=x(n)+A;

subplot(2,1,1)
stem(n,x(n))
grid
title("Señal original x[n]")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','x[n]',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

subplot(2,1,2)
stem(n,g_n)
grid
title("g[n]=x[n]+A")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','g[n]',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

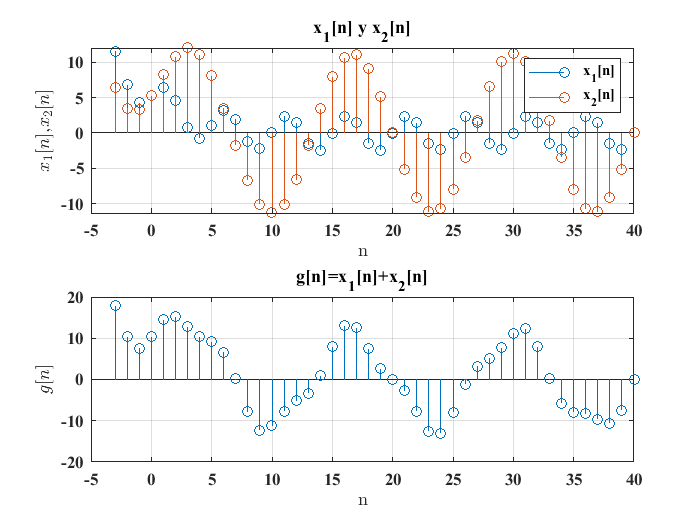
Suma de dos señales

Dadas dos señales \(x_1[n]\) y \(x_2[n]\), se obtiene una señal \(g[n]\) al sumar ambas señales individuales, esta operación significa sumar el valor de cada una de las dos señales en cada indice de muestra de tiempo \(n\):

clear
close all
n = [-3:1:40];
x1 = @(n) 2.5*sin(0.4*pi*n)+5.25*exp(-0.25*n).*cos(0.145*n);
x2 = @(n) 11.25*sin(0.15*pi*n)+5.25*exp(-0.5*n).*cos(0.245*n);

g_n=x1(n)+x2(n);

subplot(2,1,1)
stem(n,x1(n))
hold on
stem(n,x2(n))
grid
title("x_1[n] y x_2[n]")
legend("x_1[n]","x_2[n]")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1[n]$,$x_2[n]$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 


subplot(2,1,2)
stem(n,g_n)
grid
title("g[n]=x_1[n]+x_2[n]")

 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g[n]$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

Modelado de señales discretas definidas a pedazos

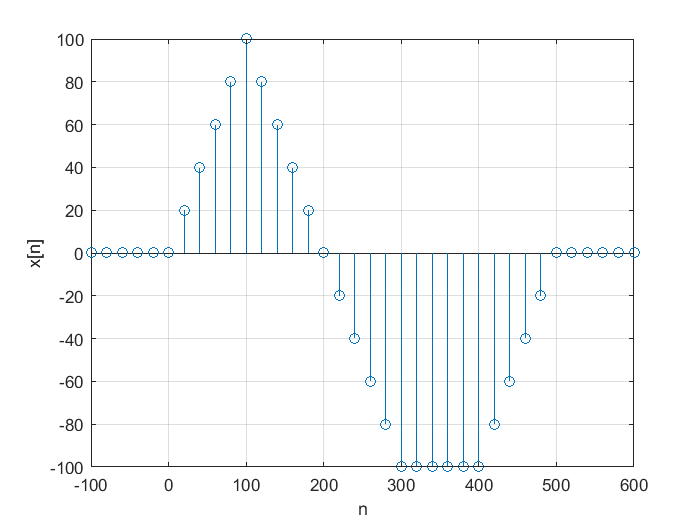
Se dice que una señal es definida a pedazos si es continua en un intervalo dado si está definida en ese intervalo y además, las expresiones matemáticas que describen o modelan a dicha señal son funciones son continuas en ese intervalo. Adicionalmente, se cumple que no hay discontinuidad en ningún punto extremo de los subintervalos. Una función contínua a pedazos se define por medio de un conjunto de expresiones, utilizando una llave, funciones locales e intervalos. Por ejemplo, considere la función continua a pedazos definida en la siguiente expresión:

(15)\[\begin{split}\begin{equation} g[n]= \left\{ \begin{array}{lcc} n & si & 0 \leq n \leq 1 \\ \\ -(n-2) & si & 1 < n \leq 3 \\ \\ -1 & si & 3 < n < 4 \\ \\ n-5 & si & 4< n \leq 5 \end{array} \right. \end{equation}\end{split}\]

Como puede observarse, los subintervalos se pueden definir en MATLAB:

figure
n=[-100:20:600];
x=@(n) n.*((n>=0)&(n<=100))-(n-200).*((n>100)&(n<=300))-100*((n>300)&(n<=400))+(n-500).*((n>400)&(n<=500));

stem(n,x(n));
xlabel("n");
ylabel("x[n]")
grid;

Ejercicio

Encuentre las funciones:

\[\begin{split} \begin{eqnarray} g_1[n]=15x[n]-10\\ g_2[n]=-13x[n]+20 \end{eqnarray} \end{split}\]

Encuentre las funciones

\[\begin{split} \begin{eqnarray} g_3[n]=15x_2[n]-15\\ g_4[n]=-13x_2[n]+20x[n] \end{eqnarray} \end{split}\]

para \(x_2[n]\) definida como:

(16)\[\begin{split}\begin{equation} x_2[n]= \left\{ \begin{array}{lcc} 50 & si & 0 \leq n \leq 200 \\ \\ n^2-n+100 & si & 200 < n \leq 500 \\ \\ -40n-15 & si & 500 < n < 700 \\ \\ 0 & si & 700 \leq n \end{array} \right. \end{equation}\end{split}\]

Suma de dos funciones contínuas a pedazos

Para hacer la suma de dos o mas funciones continuas a pedazos se opta por la representación usando llaves de las funciones. Si se tienen las gráficas de las señales, se obtiene el modelo de las señales a partir de las gráficas de las funciones. Para ilustrar esto, considérense las funciones \(x_1(t)\) y \(x_2(t)\) definidas por las gráficas:

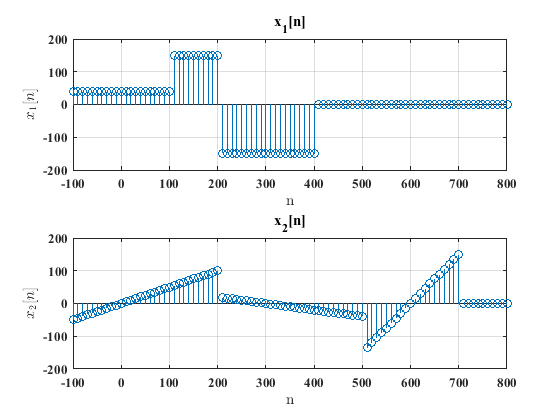
De acuerdo con las gráficas mostradas, los modelos matemáticos de las señales \(x_1(t)\) y \(x_2(t)\) son:

(17)\[\begin{split}\begin{equation} x_1[n]= \left\{ \begin{array}{lcc} 40 & si & -100 \leq n \leq 100 \\ \\ 150 & si & 100 < n \leq 200 \\ \\ -150n & si & 200 < n < 400 \\ \\ 0 & si & 400 \leq n \end{array} \right. \end{equation}\end{split}\]

En cuanto a la señal \(x_2[n]\), esta se define como:

(18)\[\begin{split}\begin{equation} x_2[n]= \left\{ \begin{array}{lcc} 0.5n & si & -100 \leq n \leq 200 \\ \\ -0.2(n-300) & si & 200 < n \leq 500 \\ \\ 1.5(n-600) & si & 500 < n < 700 \\ \\ 0 & si & 700 \leq n \end{array} \right. \end{equation}\end{split}\]

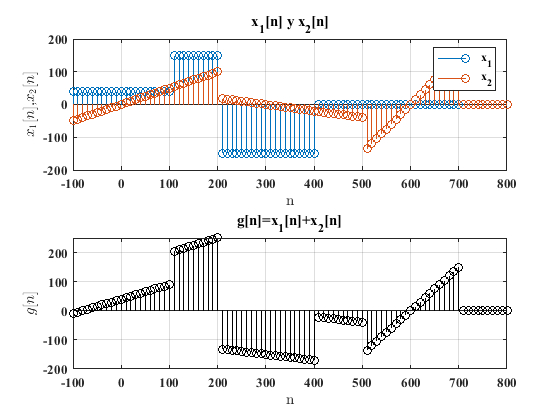
La suma de las señales \(x_1\) y \(x_2\) resulta en una tercera función \(g[n]\) que se puede construir considerando el valor de la función en cada segmento como a continuación se describe:

\[\begin{split} \begin{equation} g[n]=x_1[n]+\textcolor{red}{x_2[n]}= \left\{ \begin{array}{lcc} 40+\textcolor{red}{0.5n} & si & -100 \leq n \leq 100 \\ \\ 150+\textcolor{red}{0.5n} & si & 100 < n \leq 200 \\ \\ -150n-\textcolor{red}{0.2(n-300)} & si & 200 < n < 400 \\ \\ 0-\textcolor{red}{0.2(n-300)} & si & 400 \leq n < 500 \\ \\ \textcolor{red}{1.5(n-600)} & si & 500 \leq n < 700 \\ \\ \textcolor{red}{0} & si & 700 \leq n \end{array} \right. \end{equation} \end{split}\]

la gráfica de \(g[n]\) se obtiene usando MATLAB con el código siguiente:

clear
close all
n = [-100:10:800];
x1 = @(n)  40*((n>=-100)&(n<=100))+150*((n>100)&(n<=200))-150*((n>200)&(n<=400));
x2 = @(n)  0.5*n.*((n>=-100)&(n<=200))-0.2*(n-300).*((n>200)&(n<=500))+1.5*(n-600).*((n>500)&(n<=700));

g_n=x1(n)+x2(n);

subplot(2,1,1)
stem(n,x1(n))
grid
hold on
stem(n,x2(n))
title("x_1[n] y x_2[n]")
legend("x_1","x_2")
 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$x_1[n]$,$x_2[n]$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 



subplot(2,1,2)
stem(n,g_n,"k")
grid
title("g[n]=x_1[n]+x_2[n]")

 set(gca,'defaulttextinterpreter','latex')
  
   set(get(gca,'XLabel'),'String','n',...
                    'FontName','times news roman',... %Ajustes de rótulos y formato de letra
                    'FontAngle','normal',...
                    'FontSize',20)
% 
 set(get(gca,'YLabel'),'String','$g[n]$',...
                     'FontName','times news roman',...
                     'FontAngle','normal',...
                     'FontSize',20)

 
set(gca,'fontsize',10);
set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

Ejercicio 1

Obtenga \(g_2[n]=x_1[n]x_2[n]\)

Operación de desplazamiento en el tiempo

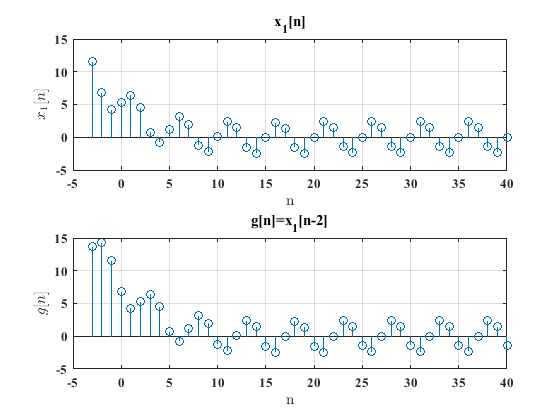
Una versión, desplazada en el tiempo de una señal dada \(x[n]\) se obtiene si se considera la expresión:

\[ g[n]=x(n-k) \]

donde \(k\) es un número entero positivo o negativo, dado que las señales discretas estan definidas solo para valores enteros del índice de muestreo \(n\). Lo anterior se muestra en la siguiente figura:

Operación de escalamiento en el tiempo

Una versión, escalada en el tiempo de una señal discreta dada \(x[n]\) se obtiene si se considera las expresiones:

\[\begin{split} \begin{eqnarray} \nonumber g[n]=x[kn]\\ g[n]=x\left [ \frac{n}{k} \right ]\\ \end{eqnarray} \end{split}\]

donde \(k\) es un número entero. Lo anterior se muestra en la siguientes figuras:

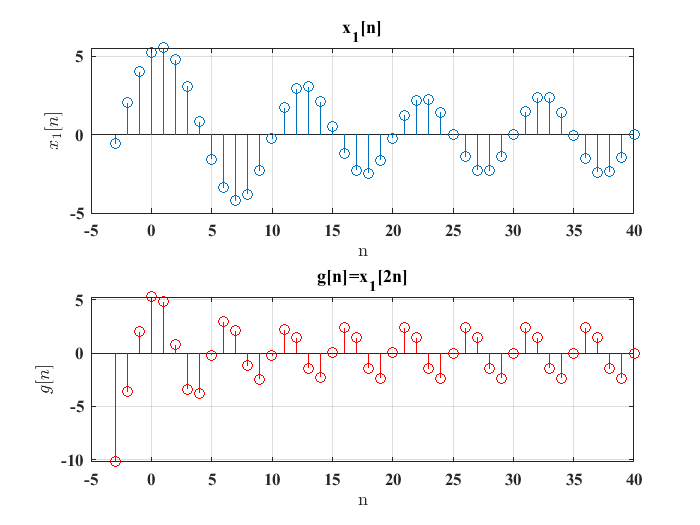
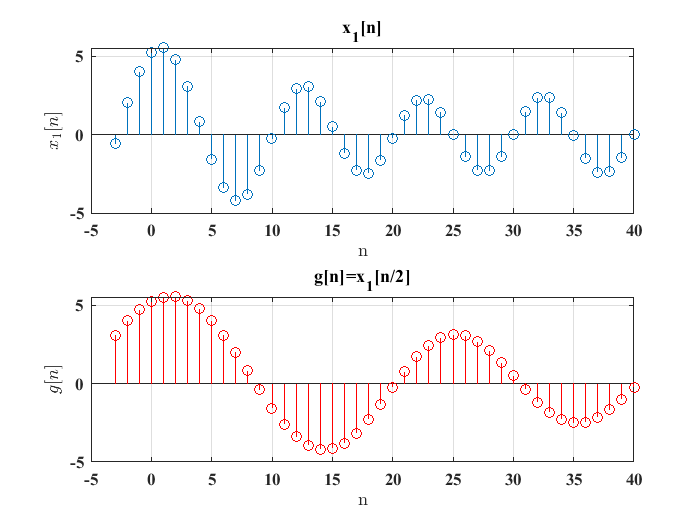
Ejercicio 2

Dada \(x[n]=25sen(0.4n)+52.5e^(-2.5n)cos(0.145n)\) obtenga:

• \[ g_1[n]=x(t-15) \]
• \[ g_2[n]=x[1.5n] \]

Operación inversión en el tiempo

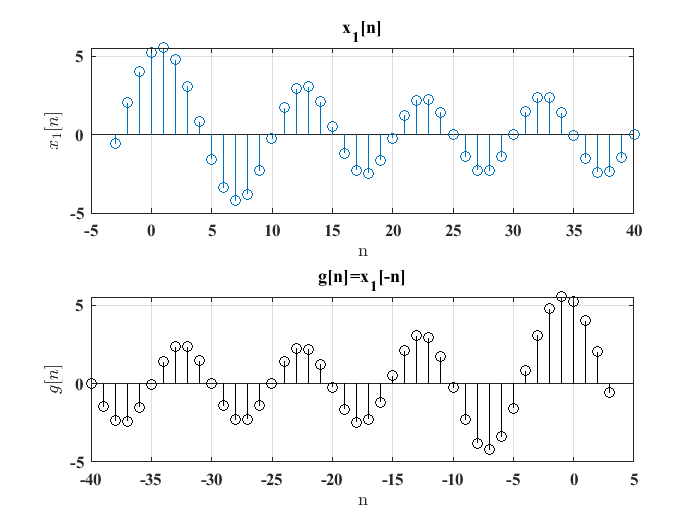
Se obtiene una versión con la característica de inversión en el tiempo mediante la siguiente expresión:

\[ y[t]=x(-n) \]

como se ilustra en la siguiente figura:

Esta operación en particular se aplica en operaciones más complejas como la convolución que se expone más adelante en el curso. Las siguientes líneas de código generan la versión invertida en el tiempo de la función

\[ x_1[n]=2.5sen(0.2\pi n)+5.25e^{-0.15n}cos(0.45n) \]

gráficamente se tiene: