Ecuaciones diferenciales y sistemas lineales.

Un método para representar la relación que existe entre las entradas y las salidas en los sistemas es una ecuación diferencial. A diferencia de las ecuaciones con incógnitas reales o complejas, las ecuaciones diferenciales tienen como incógnita a una función. Una ecuación diferencial en el contexto de los sistemas, involucra a las señales de entrada y salida, así como diversas derivadas de cualquiera de ellas o de ambas. Por ejemplo, la ecuación diferencial:

(24)\[\begin{equation} 2\frac{d^2y(t)}{dt^2}+5x(t)+300y(t)=4.5x(t) \end{equation}\]

La solución a la ecuación diferencial es la salida del sistema \(y(t)\), es decir, es aquella función que satisface la igualdad establecida en la transformación o estructura (24). En el caso de los sistemas mecánicos \(x(t)\) representará la evolución en el tiempo de una fuerza de entrada, en forma de par o empuje. En sistemas en los que existan almacenes de energía cinética en forma de masas, es común usar tambien aceleración. En el caso de los sistemas eléctricos, los alamacenes de energía son los inductores o bobinas y los capacitores y la entrada son variables como los voltajes o corrientes. Es posible encontrar análogos muy útiles entre los sistemas mecánicos y eléctricos debido a su comportamiento y las realciones constitutivas que se usan para construir la estructura de la ecuación diferencial que los modelan. Ejemplos de relaciones constitutivas para los sistemas mecánicos, de acuerdo con la ley de Newton son:

(25)\[\begin{equation} m\frac{d^2x(t)}{dt^2}=ma~~F_b=b\frac{dx(t)}{dt}~~F_r=kx(t) \end{equation}\]

Donde \(m\) es la masa en \([kg]\), \(b\) la constante de amortiguador con unidades \([Ns/m]\) y \(k\) en unidades \([N/m]\). Las fuerzas \(F_b\) y \(F_r\) son las fuerzas del amortiguador y la fuerza del resorte respectivamente. Además, de acuerdo con los conceptos de la cinemática, se sabe que la aceleración es la segunda derivada de la posicion y la velocidad es la razón de cambio o derivada de la posición \(a=\frac{d^2x(t)}{dt}\) y \(v=\frac{dx(t)}{dt}\). La Figura 4 muestra un típico sistema masa resorte amortiguador:

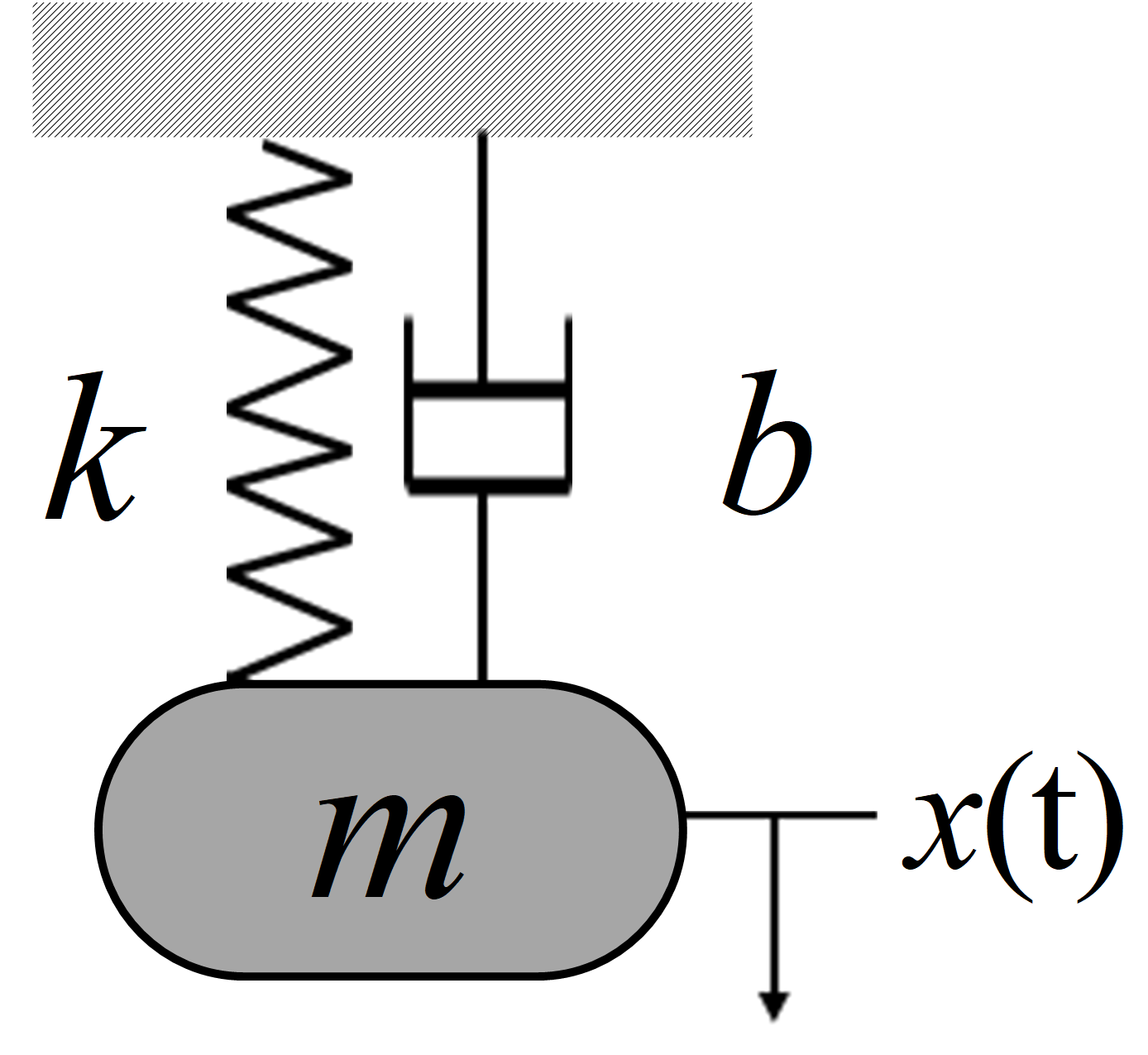
Figura 4 Sistema masa resorte amortiguador.

Aplicando la segunda ley de Newton al sistema masa resorte amortiguador se obtiene la ecuación diferencial o el modelo del sistema masa resorte amortiguador:

(26)\[\begin{equation} m\frac{d^2x(t)}{dt^2}+b_1\frac{dx(t)}{dt}+k_1x(t)=f(t) \end{equation}\]

En este caso, la salida se nombra \(x(t)\) dado que es un desplazamiento causado por la fuerza de entrada \(f(t)\), que sería equivalente a la función estímulo o de entrada, se dice entoces que para este sistema, la entrada es una fuerza y la salida un desplazamiento.

Nota

Es común usar la notación abreviada para las ecuaciones diferenciales:

\[ \frac{d^2x(t)}{dt^2}=\ddot{x}~~\frac{x(t)}{dt}=\dot{x} \]

Usando esta notación se obtiene la forma alternativa de la ecuación diferencial de movimiento o modelo matemático del sistema masa resorte amortiguador como:

\[ m\ddot{x}+b\dot{x}+kx=f \]

Para el caso de un sistema eléctrico del tipo resistencia capacitor inductancia, como el mostrado en la Figura 5

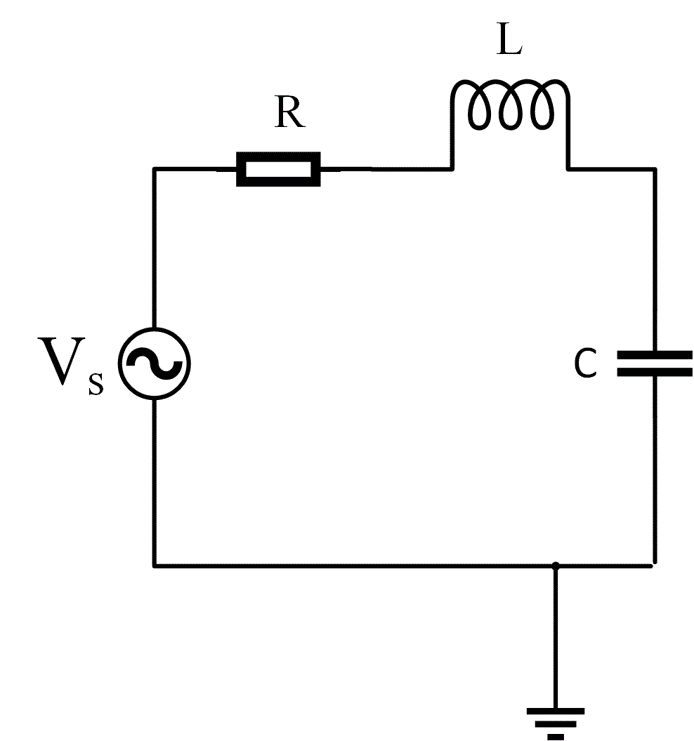
Figura 5 Circuito RLC.

Las relaciones constitutivas del sistema eléctrico son:

(27)\[\begin{equation} v_L=L\frac{di(t)}{dt}~~i_C=C\frac{dv_c(t)}{dt}~~v_R=i(t)R \end{equation}\]

Con \(L\) la inductancia en \([H]\), \(C\) la capacitancia en \([F]\) y \(R\) la resistencia en \([\Omega]\). Además, por la ley de Kirchoff, la corriente en el capacitor \(i_C(t)=i(t)\). En este caso, la salida se nombra \(v_c(t)\) el voltaje en el capacitor, debido a la presencia de la fuente de alimentación \(V_s(t)\), que sería equivalente a la función estímulo o de entrada. La ecuación diferencial que modela a este sistema eléctrico es:

(28)\[\begin{equation} LC\frac{d^2v_c(t)}{dt^2}+RC\frac{dv_c(t)}{dt}+v_c(t)=V_s(t) \end{equation}\]