Propiedades de la transformada de Laplace.

La transformada de Laplace, definida en la ecuación (66) genera una superficie en el espacio \(\mathbb{R}^3\), cuando se grafica su magnitud. El siguiente código de MATLAB genera dicha superficie, para la transformada de Laplace bilateral, es decir para la transformada de Laplace definida para \({-\infty}<t<{\infty}\).

clear 
close all
[s_real,s_imaginaria] = meshgrid([-5:0.3:5],[-20:0.5:20]);
s = s_real+j*s_imaginaria; %Definición de la variable compleja s=real+imaginaria
Xs = @(s) (1)./(2.5*s.^2+3*s+350);  % Transformada de Laplace de la salida de un sistema
MagXs = abs(Xs(s));

% Se define un rango de frecuencias de interés.
omega = [-25:0.1:25];
tr = j*omega;
% Se produce una retícula para generar la superficie
%shading interp;
%colormap copper;
m1 = mesh(s_real,s_imaginaria,MagXs);
hold on;
% Se superpone la curva de magnitud de X(s)
%  usando el comando plot3().
m2 = plot3(real(tr),imag(tr),abs(Xs(tr)),'b','LineWidth',1.5);
set(gcf,'Visible','on')
hold off;
axis([-5,5,-25,25]);
% Se especifican los rótulos para los ejes x,y y z.
xlabel('\sigma');
ylabel('j\omega');
zlabel('|X(s)|');
% Se especifica un ángulo de mejor visualización. 
view(gca,[23.5,38]);
set(gca,'fontsize',20);
%set(gca,'fontname','Times New Roman','FontWeight','Bold'); 

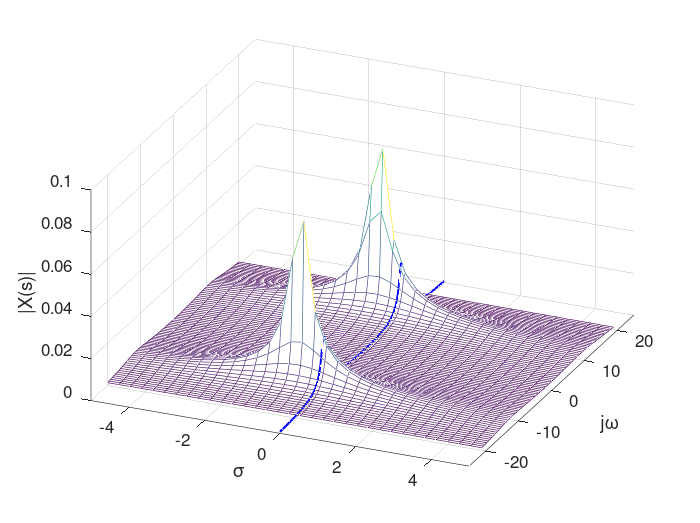
Como es claro en la gráfica anterior, la variable compleja \(s\) tiene un caso particular cuando la parte real de \(s\) es idénticamente cero, es ese caso, la transformada de Laplace se convierte en la transformada de Fourier. Algunas propiedades interesantes de la transformada de Laplace se presentan a continuación:

Linealidad de la Transformada de Laplace

La transformada de Laplace es un operador lineal, de ahí que cobre una importancia particular en la ingeniería. El principio de superposición aplica a la transormada de Laplace y, por ende sustenta la propiedad de linealidad del operador transformadad como se indica a continuación:

Principio de linealidad de la transformada de Laplace:

(69)\[ k_1 x_1(t)+k_2 x_2 (t)\xrightarrow{\mathscr{L}} k_1X_1(s)+k_2X_2(s)\]

Ejemplo: la transformada de Laplace de la función \(x(t)=2.8cos(2t)+5.4e^{-3t}+3.5sen(5t)\)

\[\begin{split} \begin{eqnarray} &X(s)=\mathscr{L} \left \{ x(t) \right\}= 2.8\mathscr{L} \left \{ cos(2t) \right\}+5.4\mathscr{L} \left \{ e^{-3t} \right\}+3.5\mathscr{L} \left \{ sen(5t) \right\}\\ &X(s)=\frac{2.8s}{s^2+4}+\frac{5.4}{s+3}+\frac{87.5}{s^2+25} \end{eqnarray} \end{split}\]

Propiedad de desplazamiento en el tiempo

Un desplazamiento en el tiempo, aplicado a una función \(x(t)\) en el dominio del tiempo, por medio de una constante arbitraria \(\tau\), corresponde al producto de la transformada de Laplace de \(x(t)\) con el factor \(e^{-\tau s}\):

Propiedad de desplazamiento en el tiempo de la transformada de Laplace:

(70)\[\mathscr{L} \left \{ x(t-\tau) \right\} \xrightarrow{\mathscr{L}} e^{-\tau s} X(s)\]

Ejemplo: la transformada de Laplace de la función \(x(t)=0.01cos(2(t-3))\)

\[ \mathscr{L} \left \{ 0.01cos(2(t-3)) \right\} = \frac{se^{-3\tau s}}{s^2+4} \]

Propiedad de desplazamiento en el dominio de \(s\)

Dada una función \(x(t)\), la transformada de Laplace del producto de tal función con el factor \(s_0\) implica que la transformada de Laplace de \(x(t)\), sea desplazada \(s_0\) veces en el dominio complejo.

Propiedad de desplazamiento en el dominio de \(s\) de la transformada de Laplace:

(71)\[\mathscr{L} \left \{ x(t)e^{s_0t} \right\} \xrightarrow{\mathscr{L}} X(s-s_0)\]

Ejemplo: la trasfomdada de Laplace de la función \(x(t)=e^{-0.5t}sen(6\pi t)\)

\[ \mathscr{L} \left \{ e^{-0.5t}cos(6\pi t) \right\} = \frac{6\pi(s+0.5)}{(s+0.5)^2+36\pi^2} \]

Propiedad de escalamiento en los dominios de \(s\) y de \(t\)

Una operación de escalamiento de una función \(x(t)\), que produce una función \(g(t)=x\left( \frac{t}{a}\right )\) tendrá como resultado una función escalada e el dominio de \(s\), con escalamiento inverso:

Propiedad de escalamento en el tiempo y la frecuencia de la transformada de Laplace:

(72)\[\mathscr{L} \left \{ x(at) \right\} \xrightarrow{\mathscr{L}} \frac{1}{|a|} X\left ( \frac{s}{a} \right )\]

Ejemplo: la trasfomdada de Laplace de la función \(x(t)=cos \left ( 2\pi\frac{t}{3} \right )\)

\[ \mathscr{L} \left \{ cos \left ( 2\pi\frac{t}{3} \right ) \right \} = 3\frac{3s}{9s^2+4\pi^2} \]

Diferenciación en el dominio del tiempo

Dada una función \(x(t)\), la transformada de Laplace de su derivada se expresa como:

Propiedad de diferenciación en el dominio del tiempo:

(73)\[\mathscr{L} \left \{ \frac{dx(t)}{dt} \right\} \xrightarrow{\mathscr{L}} sX(s)\]

Por ejemplo para la transformada de la función \(\frac{d\left (3cos(4\pi t)\right )}{dt}\) se tiene que:

\[ \mathscr{L} \left \{ \frac{d\left (3cos(4\pi t)\right )}{dt} \right \} = s\mathscr{L} \left \{ 3cos(4\pi t)\right \}=\frac{3s^2}{s^2+16\pi^2} \]

Diferenciación en el dominio de \(s\)

Dada una función \(x(t)\), la operación producto de \(x(t)\) con la variable independiente \(t\), implica diferenciación o derivada en el dominio de \(s\) de su transformada \(X(s)\).

Propiedad de diferenciación en el dominio de \(s\):

(74)\[\mathscr{L} \left \{ tx(t) \right\} \xrightarrow{\mathscr{L}} -\frac{dX(s)}{ds}\]

Por ejemplo, para la función \(x(t)=te^{-3t}\), se usa la propiedad de diferenciación en el dominio del tiempo como:

\[ \mathscr{L} \left \{ te^{-3t} \right \} = -\frac{\mathscr{L} \left \{ e^{-3t} \right\}}{ds} =\frac{d \left ( \frac{1}{s+3} \right ) }{ds}=\frac{1}{(s+3)^2} \]

Propiedad de integración

Dada la integral de una función \(x(t)\), la transformada de la integral, al ser la operación inversa de la diferenciación se expresa como:

Propiedad de integración:

(75)\[\mathscr{L} \left \{ \int^{t}_{-\infty}x(\tau)d\tau \right\} \xrightarrow{\mathscr{L}} \frac{1}{s}X(s)\]