Práctica 1: Comprobación de linealidad con MATLAB

En esta práctica se comprueba la propiedad de linealidad para sistemas, en forma de estructura \(Transf\{x(t)\}\) para los sistemas:

\[\begin{split} \begin{eqnarray} &y(t)=2.5x(t)\\ &y(t)=4.5x(t)-3\\ &y(t)=(x(t))^2-5x(t)+2\\ &y(t)=cos(3x(t))+2x(t)\\ &y(t)=e^{(-4.5x(t))}cos(20x(t)) \end{eqnarray} \end{split}\]

Con dos funciones impulso arbitrarias \(x_1(t)=sen(2\pi t)\) y \(x_2=e^{-4t}cos(3.5t)\). Para realizar la prueba de linealidad, se utiliza el código siguiente:

clear
close all
t = [0:0.01:4];               % Vector de tiempo
x1 = sin(2*pi*t);           % Tseñal 1
x2 = exp(-0.5*t).*cos(3.5*t);             % señal 2
k1 = 4.5;                   % constante k1
k2 = 5.25;                %   constante k2
x = k1*x1+k2*x2;      % Señal combinada
% Se deinen las funciones Transf para el sistema
Transf_a = @(x) 2.5*x;
Transf_b = @(x) 4.5*x+3;
Transf_c = @(x) x.^2-5*x+2;
Transf_d = @(x) cos(3*x)+2*x;
Transf_e = @(x) exp(-4.5*x).*cos(20*x);
% Prueba de linealidad
y1 = Transf_a(x1);
y2 = Transf_a(x2);
y_esperada= k1*y1+k2*y2;  % Respuesta esperada para un sistema lineal
y_real = Transf_a(x);             % Respuesta real del sistema
clf;                          % Limpiar figura
subplot(1,2,1);               
plot(t,y_esperada);                % Se grafica la respuesta esperada
title('y_{esp} = k_1 y_1 + k_2 y_2') 
xlabel('t (segundos)');
ylabel('Amplitud');
subplot(1,2,2);
plot(t,y_real);                % Se grafica la respuesta real   
title('y_{real} = Transf\{k_1 x_1 + k_2 x_2\}') 
xlabel('t (segundos)');
ylabel('Amplitud');
figure
plot(t,y_esperada);
hold on
plot(t,y_real,'k--');  
title('Comparación') 
xlabel('t (segundos)');
ylabel('Amplitud');
legend("y_{esp} = k_1 y_1 + k_2 y_2","y_{real} = Transf\{k_1 x_1 + k_2 x_2\}")

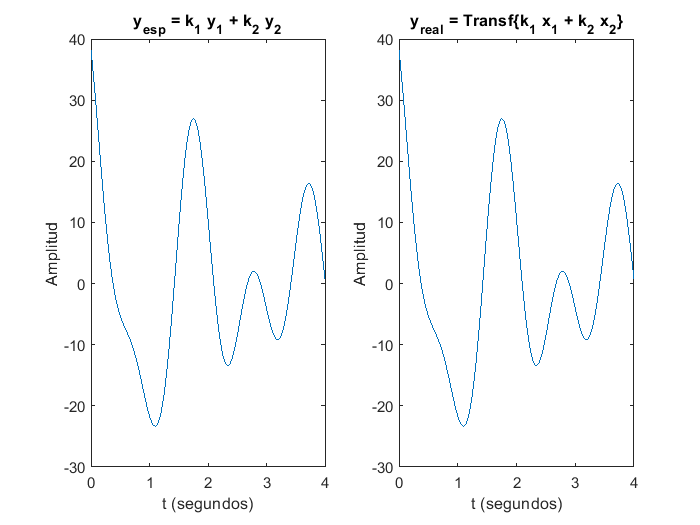
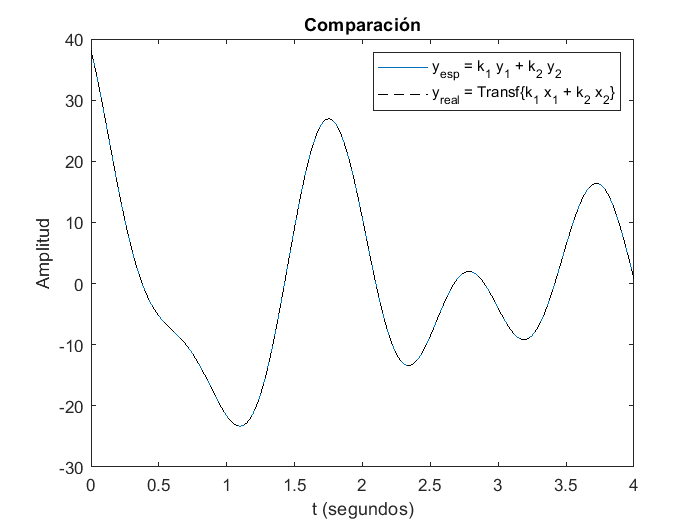
Como es posible observar en la gráfica anterior, el sistema \(y(t)=2.5x(t)\) es lineal, dado que cumple con el principio de superposición, dado que las gráficas de \(y_{esperada}\) y \(y_{real}\) son exactamente las mismas, si el mismo código se ejecuta, pero esta vez evaluando el sistema definido como \(y(t)=x(t)^2-5x(t)+2\) se obtiene:

clear
close all
t = [0:0.01:4];               % Vector de tiempo
x1 = sin(2*pi*t);           % Tseñal 1
x2 = exp(-0.5*t).*cos(3.5*t);             % señal 2
k1 = 4.5;                   % constante k1
k2 = 5.25;                %   constante k2
x = k1*x1+k2*x2;      % Señal combinada
% Se deinen las funciones Transf para el sistema
Transf_a = @(x) 2.5*x;
Transf_b = @(x) 4.5*x+3;
Transf_c = @(x) x.^2-5*x+2;
Transf_d = @(x) cos(3*x)+2*x;
Transf_e = @(x) exp(-4.5*x).*cos(20*x);
% Prueba de linealidad
y1 = Transf_c(x1);
y2 = Transf_c(x2);
y_esperada= k1*y1+k2*y2;  % Respuesta esperada para un sistema lineal
y_real = Transf_c(x);             % Respuesta real del sistema
clf;                          % Limpiar figura
subplot(1,2,1);               
plot(t,y_esperada);                % Se grafica la respuesta esperada
title('y_{esp} = k_1 y_1 + k_2 y_2') 
xlabel('t (segundos)');
ylabel('Amplitud');
subplot(1,2,2);
plot(t,y_real);                % Se grafica la respuesta real   
title('y_{real} = Transf\{k_1 x_1 + k_2 x_2\}') 
xlabel('t (segundos)');
ylabel('Amplitud');
figure
plot(t,y_esperada);
hold on
plot(t,y_real,'k--');  
title('Comparación') 
xlabel('t (segundos)');
ylabel('Amplitud');
legend("y_{esp} = k_1 y_1 + k_2 y_2","y_{real} = Transf\{k_1 x_1 + k_2 x_2\}")

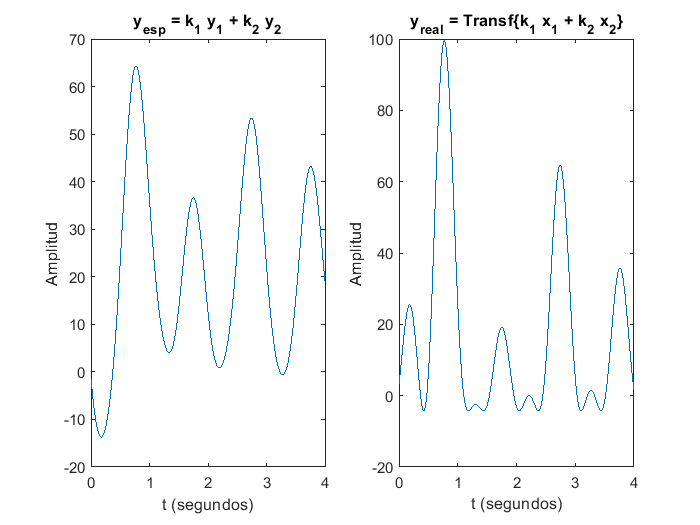
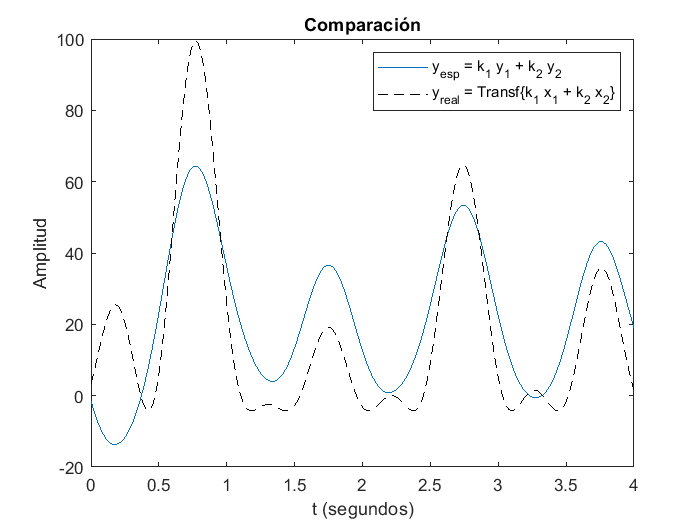
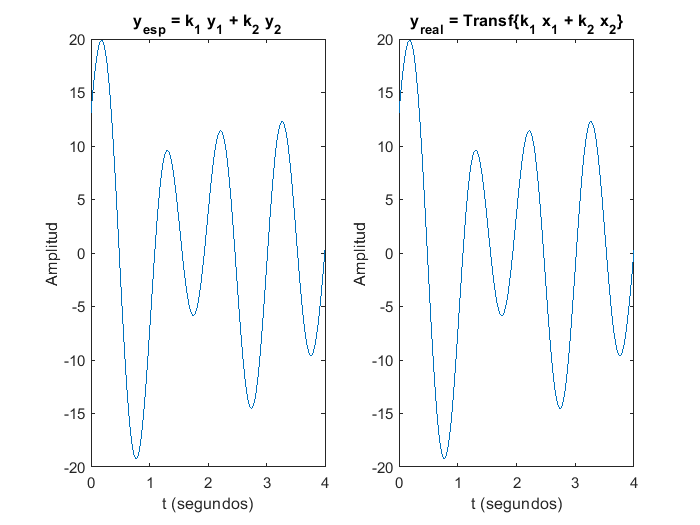
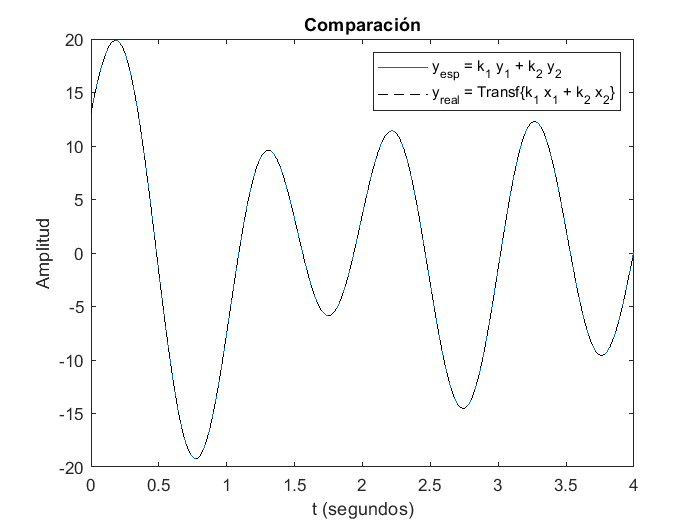
En este caso el sistema es no-lineal, dado que las gráficas de \(y_{esperada}\) y \(y_{real}\) son diferentes. Finalmente, si las constantes \(k_1\) y \(k_2\) cambian, incluso de signo, para un sistema lineal, el principio de superposición se sigue cumpliendo:

clear
close all
t = [0:0.01:4];               % Vector de tiempo
x1 = sin(2*pi*t);           % Tseñal 1
x2 = exp(-0.5*t).*cos(3.5*t);             % señal 2
k1 = -4.5;                   % constante k1
k2 = 15.25;                %   constante k2
x = k1*x1+k2*x2;      % Señal combinada
% Se deinen las funciones Transf para el sistema
Transf_a = @(x) 2.5*x;
Transf_b = @(x) 4.5*x+3;
Transf_c = @(x) x.^2-5*x+2;
Transf_d = @(x) cos(3*x)+2*x;
Transf_e = @(x) exp(-4.5*x).*cos(20*x);
% Prueba de linealidad
y1 = Transf_a(x1);
y2 = Transf_a(x2);
y_esperada= k1*y1+k2*y2;  % Respuesta esperada para un sistema lineal
y_real = Transf_a(x);             % Respuesta real del sistema
clf;                          % Limpiar figura
subplot(1,2,1);               
plot(t,y_esperada);                % Se grafica la respuesta esperada
title('y_{esp} = k_1 y_1 + k_2 y_2') 
xlabel('t (segundos)');
ylabel('Amplitud');
subplot(1,2,2);
plot(t,y_real);                % Se grafica la respuesta real   
title('y_{real} = Transf\{k_1 x_1 + k_2 x_2\}') 
xlabel('t (segundos)');
ylabel('Amplitud');
figure
plot(t,y_esperada);
hold on
plot(t,y_real,'k--');  
title('Comparación') 
xlabel('t (segundos)');
ylabel('Amplitud');
legend("y_{esp} = k_1 y_1 + k_2 y_2","y_{real} = Transf\{k_1 x_1 + k_2 x_2\}")