Función de transferencia.

Como se trató en secciones anteriores, la integral de convolución (60) permite encontrar la respuesta de los sistemas lineales e invariantes en el tiempo a partir del conocimiento de su respuesta al impulso. En general, sabemos que la respuesta \(y(t)\) de un sistema dinámico, modelado por medio de una ecuación diferencial de un orden arbitrario, se encuentra al encontrar la función solución a dicha ecuación diferencial. El modelo general de un sistema lineal, invariante en el tiempo adquiere la forma:

(76)\[a_n\frac{d^ny}{dt^n}+ a_{n-1}\frac{d^{n-1}y}{dt^{n-1}}+...+a_2\frac{d^2y}{dt^2}+ a_1\frac{dy}{dt}+a_0y=b_m\frac{d^mx}{dt^m}+ b_{m-1}\frac{d^{m-1}x}{dt^{m-1}}+...+b_2\frac{d^2x}{dt^2}+ b_1\frac{dx}{dt}+b_0x\]

Donde los coeficientes \(a_n\) y \(b_n\) son constantes, además \(m\) y \(n\) son enteros positivos, usualmente se considera que \(n>m\). Como se ha comprobado en secciones antariores, la transformada de Laplace permite encontrar la función solución, algebrizando el problema de cálculo, es decir convierte a la funcion \(y(y)\) en una función que aparace de forma algebraica, es decir, de forma que puede ser despejada o expresada en términos de \(a_n\), \(b_n\) y \(X(s)\). De maneta que al aplicar la transformada de Laplace a la ecuación diferencial, considerando todas las condiciones iniciales iguales a cero:

(77)\[a_ns^{n}Y(s)+ a_{n-1}s^{n-1}Y(s)+...+a_1sY(s)+a_0Y(s)=b_ms^{m}X(s)+ b_{m-1}s^{m1}X(s)+...+b_1sX(s)+b_0X(s)\]

Es posible entonces despejar \(Y(s)\):

(78)\[Y(s)=\frac{b_ms^{m}+ b_{m-1}s^{m-1}+...+b_2s^2+ b_1s+b_0}{a_ns^{n}+ a_{n-1}s^{n-1}+...+a_2s^2+ a_1s+a_0}X(s)\]

Si se realiza una representación alternativa de la ecuación (78) en forma de un cociente se obtiene:

(79)\[\frac{Y(s)}{X(s)}=\textcolor{red}{\frac{b_ms^{m}+ b_{m-1}s^{m-1}+...+b_2s^2+ b_1s+b_0}{a_ns^{n}+ a_{n-1}s^{n-1}+...+a_2s^2+ a_1s+a_0}}\]

La expresion en color rojo no depende en absoluto del estímulo o perturbación \(X(s)\), solo depende de los coeficientes de la ecuación diferencial, que son los que determinan las características del sistema en su estructura como transformación. A este cociente se le conoce como la Funcion de transferencia del sistema. En esta función, como ya se ha mencionado la variable independiente es \(s=\sigma+j\omega\), con \(j=\sqrt{-1}\), además considérese que \(\sigma\) y \(\omega\) son números reales.

En la función de transferencia expresada en la (79), las raices del numerador son los ceros del sistema y las raices del denominador se conocen como los polos del sistema. En sistemas eléctricos y mecánicos, estos polos están íntimamente relacionados con las resonancias o frecuencias naturales del sistema. Dado que la función de transferencia tiene una analogía con el concepto de ganancia, que es muy utilizado en ingeniería electrónica para describir el desempeño de los amplificadores, en ocaciones a la función de transferencia se le denota como \(G(s)\), de manera que la salida \(Y(s)\) se puede expresar como:

\[ Y(s)=G(s)X(s) \]

Esta última expresión indica que la entrada \(X(s)\), al ser multiplicada por la ganancia \(G(s)\) produce la salida \(Y(s)\). Si se sustituye en la ecuación (79) el caso particular cuando la parte real de la variable compeja \(s\) es igual a cero, es decir, se sustituye \(s=j\omega\). Se obtiene la función de respuesta en frecuencia del sistema.

Función de respuesta en frecuencia.

Como un ejemplo de aplicación de la función de respuesta en frecuencia, analizaremos nuevamente al sistema masa resorte amortiguador mostrado en la Figura 8 y cuyos parámetros se presentan en la Tabla 6,con las condiciones iniciales \(x(0)=0~[m]\) y \(\dot{x}(0)=0~[m/s]\)

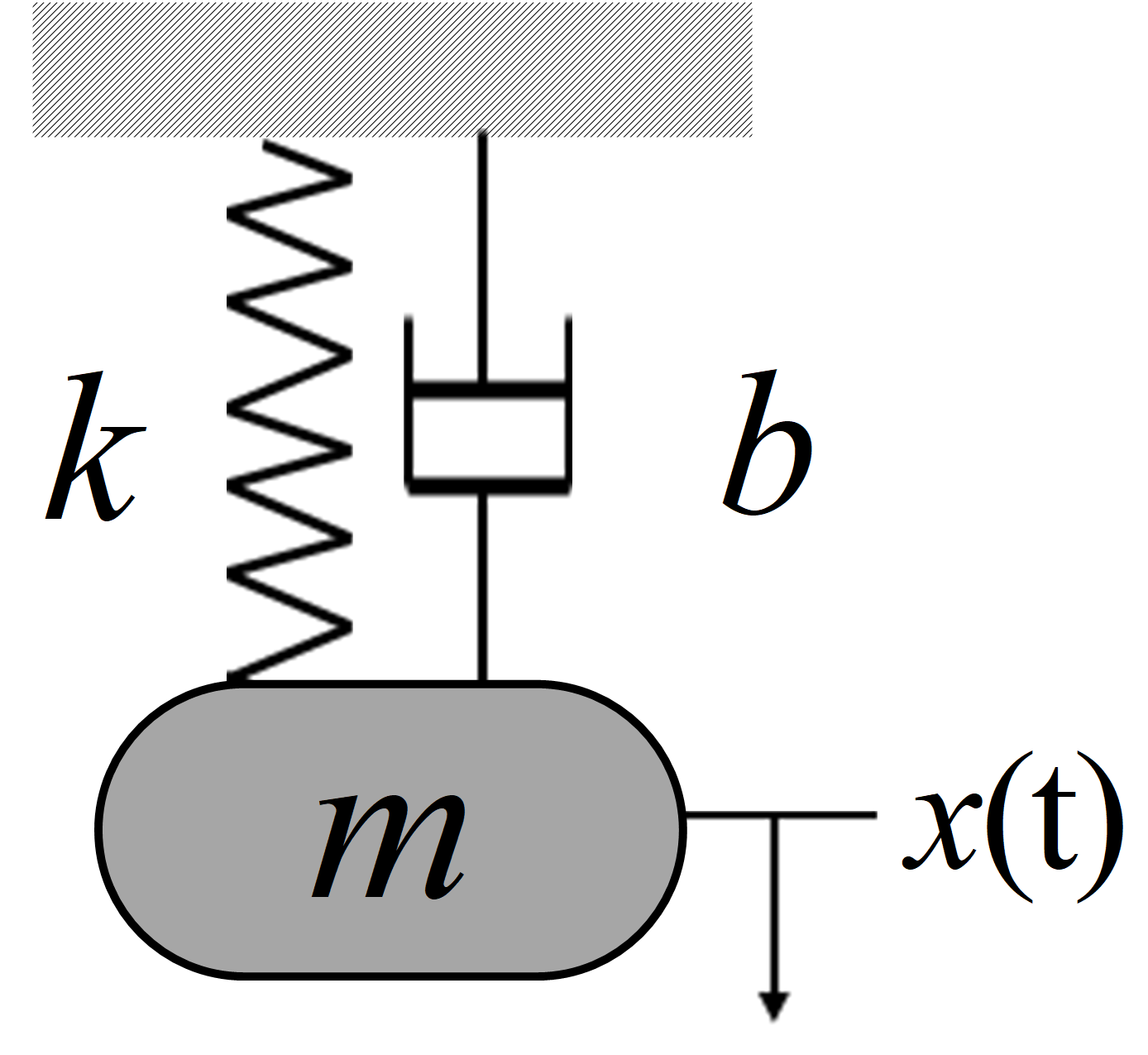
Figura 8 Sistema masa resorte amortigador.

Tabla 6 Tabla de parámetros del sistema masa resorte amortiguador

\[Parámetro\]	\[Valor\]
\[m\]	\[4.3~[kg]\]
\[b\]	\[1.5~[Ns/m]\]
\[k\]	\[430~[N/m]\]

En este caso, la ecuación diferencial, se encuentra sustituyendo los valores de \(m\), \(b\) y \(k\) para obtener:

(80)\[\begin{equation} 4.3\frac{d^2x(t)}{dt^2}+1.5\frac{dx(t)}{dt}+430x(t)=f(t) \end{equation}\]

Si \(f(t)=cos(\omega_0t)\) se obtiene la función de transferencia:

(81)\[\begin{equation} \frac{X(s)}{F(s)}=\frac{1}{4.3s^{2}+1.5s+430} \end{equation}\]

La función de respuesta en frecuencia del sistema se obtiene al sustituir \(s=j\omega\) en la función de transferencia:

(82)\[\begin{equation} X(j\omega)=\frac{1}{4.3(j\omega)^{2}+1.5(j\omega)+430} \end{equation}\]

Dado que \(j=\sqrt{-1}\):

\[ X(j\omega)=\frac{1}{4.3(\sqrt{-1}\omega)^2+1.5\sqrt{-1}\omega+430}=\frac{1}{-4.3\omega^2+1.5j\omega+430}=\frac{1}{\omega(1.5j-4.3\omega)+430} \]

En MATLAB se puede encontrar una gráfica para un rango de frecuencias \(\omega\) de interés. Por ejemplo la gráfica de la respuesta en frecuencia del sistema masa-resorte-amortiguador se obtiene usado las instrucciones:

omega=[0.1:0.01:20];
Xw=1./(omega.*(1.5*i-4.3*omega)+430);
plot(omega,abs(Xw))
title("Función de respuesta en frecuencia")
xlabel("\omega [rad/s]")
ylabel("|X(j\omega)|")
grid

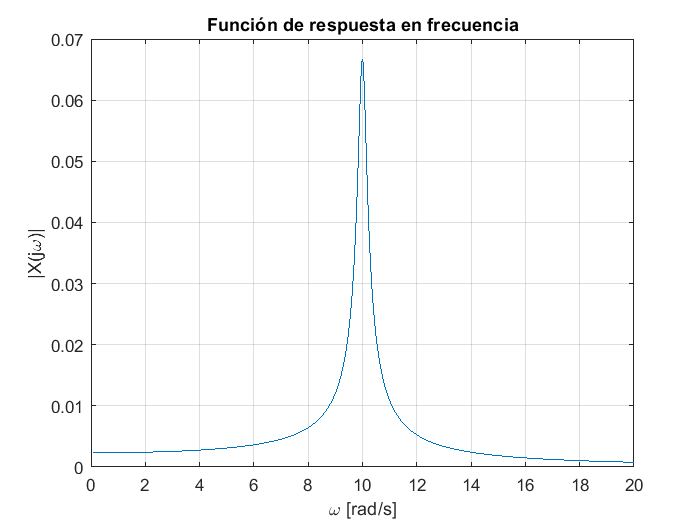
Como puede observarse, el pico de la gráfica de la función de respuesta en frecuencia coincide con el valor de la frecuencia natural del sistema \(\omega_n=\sqrt{\frac{k}{m}-\frac{b^2}{4m^2}}=\sqrt{\frac{430}{4.3}-\frac{1.5^2}{4(4.3)^2}}=9.9985~rad/s\)